
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Методические указания по выполнению домашней контрольной работыМЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО ВЫПОЛНЕНИЮ ДОМАШНЕЙ КОНТРОЛЬНОЙ РАБОТЫ по дисциплине «Математика» Для обучающихся по специальности 38.02.04 Коммерция (по отраслям) Орел, 2016 г. ЦЕЛЬ И МЕСТО ДОМАШНЕЙ КОНТРОЛЬНОЙ РАБОТЫ В УЧЕБНОМ ПРОЦЕССЕ
Учебная дисциплина «Математика» является частью основной профессиональной образовательной программы в соответствии с ФГОС СПО по специальности 38.02.04 Коммерция (по отраслям) (базовая подготовка) Дисциплина входит в математический и естественнонаучный цикл профессиональной подготовки. Цели и задачи дисциплины – требования к результатам освоения дисциплины: В результате освоения дисциплины обучающийся должен уметь: - решать прикладные задачи в области профессиональной деятельности; В результате освоения дисциплины обучающийся должен знать: - значение математики в профессиональной деятельности и при освоении основной профессиональной образовательной программы; - основные математические методы решения прикладных задач в области профессиональной деятельности; - основные понятия и методы математического анализа, дискретной математики, линейной алгебры, теории комплексных чисел, теории вероятностей и математической статистики; - основы интегрального и дифференциального исчисления; В результате освоения дисциплины обучающийся должен овладеть общими компетенциями, включающими в себя способность: ОК 2. Организовывать собственную деятельность, выбирать типовые методы и способы выполнения профессиональных задач, оценивать их эффективность и качество. В результате освоения дисциплины обучающийся должен обладать профессиональными компетенциями: ПК 1.8. Использовать основные методы и приемы статистики для решения практических задач коммерческой деятельности, определять статистические величины, показатели вариации и индексы. ПК 2.1. Использовать данные бухгалтерского учета для контроля результатов и планирования коммерческой деятельности, проводить учет товаров (сырья, материалов, продукции, тары, других материальных ценностей) и участвовать в их инвентаризации. ПК 2.9. Применять методы и приемы анализа финансово-хозяйственной деятельности при осуществлении коммерческой деятельности, осуществлять денежные расчеты с покупателями, составлять финансовые документы и отчеты. ПК 3.7. Производить измерения товаров и других объектов, переводить внесистемные единицы измерений в системные. Домашняя контрольная работа – самостоятельная работа студента, которая способствуетуглубленному изучению материала. Перед выполнением работы необходимо внимательно изучить методические рекомендации поподготовке контрольной работы, составить план работы, который должен включать основные вопросы,охватывающие в целом всю прорабатываемую тему. ВЫБОР ЗАДАНИЯ ДОМАШНЕЙ КОНТРОЛЬНОЙ РАБОТЫ
Контрольная работа по дисциплине «Математика» предусматривает выполнение 5 заданий. Вариант контрольной работы выбирается по двум последним цифрам номера студенческого билета (таблица 1). Обучающиеся должны быть внимательными при определении варианта. Работа, выполненная не по своему варианту, возвращается студенту без проверки и зачета.
ТРЕБОВАНИЯ К ОФОРМЛЕНИЮ ДОМАШНЕЙ КОНТРОЛЬНОЙ РАБОТЫ
При выполнении контрольной работы надо строго придерживаться указанных ниже правил. Работы, выполненные без соблюдения этих правил, не зачитываются и возвращаются студентам для переработки. 1. Контрольные работы выполнять в тетради чернилами любого цвета, кроме красного, оставляя поля для замечаний рецензента. В случае печатной работы – обязательно предоставление электронного варианта работы. 2. На обложке тетради должны быть ясно написаны фамилия студента, его инициалы, название дисциплины; здесь же следует указать дату сдачи работы на проверку. 3. В работу должны быть включены все задачи, указанные в задании, строго по своему варианту. Контрольные работы, содержащие не все задания, а также содержащие задачи не своего варианта, не зачитываются. 4. Решение задач надо располагать в порядке, указанном в заданиях, сохраняя номера задач.Задачи выполняются строго по порядку номеров, записывается полное условие каждого номера, аккуратно и подробно оформляется решение (с пояснениями), формулируется четкий ответ. 5. Перед решением каждой задачи надо выписать полностью её СОДЕРЖАНИЕ ДИСЦИПЛИНЫ РАЗДЕЛ 1. КОМПЛЕКСНЫЕ ЧИСЛА Тема 2.3 Ряды Числовые ряды. Свойства числовых рядов. Достаточные признаки сходимости. Знакопеременные ряды. Абсолютно и условно сходящиеся ряды. Степенные ряды. Область и радиус сходимости ряда. Ряд Тейлора и Маклорена. Разложение элементарных функций в степенные ряды. Вопросы для самоконтроля: 1. Что такое числовые ряды? 2. Перечислите свойства числовых рядов. 3. Какие ряды называются знакопеременными? 4. Перечислите признаки сходимости ряда. Таблица 1.
Варианты контрольных работ Вариант 1 №1. Решить систему трех уравнений с тремя неизвестными методами Крамера и Гаусса: №2 Определить производные а) №3 Найти интегралы: а) №4 Вычислить определенный интеграл с точностью до 0,001 путем предварительного разложения подынтегральной функции в ряд и почленного интегрирования этого ряда №5 Найти общее решение (общий интеграл) дифференциального уравнения первого порядка
Вариант 2 №1. Решить систему трех уравнений с тремя неизвестными методами Крамера и Гаусса: №2 Определить производные а)
№3 Найти интегралы: а)
№4 Вычислить определенный интеграл с точностью до 0,001 путем предварительного разложения подынтегральной функции в ряд и почленного интегрирования этого ряда №5 Найти общее решение (общий интеграл) дифференциального уравнения первого порядка
Вариант 3 №1. Решить систему трех уравнений с тремя неизвестными методами Крамера и Гаусса: №2 Определить производные а) №3 Найти интегралы:а) №4 Вычислить определенный интеграл с точностью до 0,001 путем предварительного разложения подынтегральной функции в ряд и почленного интегрирования этого ряда №5 Найти общее решение (общий интеграл) дифференциального уравнения первого порядка Вариант 4 №1. Решить систему трех уравнений с тремя неизвестными методами Крамера и Гаусса: №2 Определить производные а) г)
№3 Найти интегралы:а)
№4 Вычислить определенный интеграл с точностью до 0,001 путем предварительного разложения подынтегральной функции в ряд и почленного интегрирования этого ряда №5 Найти общее решение (общий интеграл) дифференциального уравнения первого порядка Вариант 5. №1. Решить систему трех уравнений с тремя неизвестными методами Крамера и Гаусса: №2 Определить производные
№3 Найти интегралы:а)
№4 Вычислить определенный интеграл с точностью до 0,001 путем предварительного разложения подынтегральной функции в ряд и почленного интегрирования этого ряда №5 Найти общее решение (общий интеграл) дифференциального уравнения первого порядка
Вариант 6 №1. Решить систему трех уравнений с тремя неизвестными методами Крамера и Гаусса: №2 Определить производные №3 Найти интегралы:а)
№4 Вычислить определенный интеграл с точностью до 0,001 путем предварительного разложения подынтегральной функции в ряд и почленного интегрирования этого ряда №5 Найти общее решение (общий интеграл) дифференциального уравнения первого порядка Вариант 7 №1. Решить систему трех уравнений с тремя неизвестными методами Крамера и Гаусса: №2 Определить производные
№3 Найти интегралы:а)
№4 Вычислить определенный интеграл с точностью до 0,001 путем предварительного разложения подынтегральной функции в ряд и почленного интегрирования этого ряда №5 Найти общее решение (общий интеграл) дифференциального уравнения первого порядка Вариант 8 №1. Решить систему трех уравнений с тремя неизвестными методами Крамера и Гаусса: №2 Определить производные
№3 Найти интегралы:а)
№4 Вычислить определенный интеграл с точностью до 0,001 путем предварительного разложения подынтегральной функции в ряд и почленного интегрирования этого ряда №5 Найти общее решение (общий интеграл) дифференциального уравнения первого порядка Вариант 9 №1. Решить систему трех уравнений с тремя неизвестными методами Крамера и Гаусса: №2 Определить производные
№3 Найти интегралы:а)
№4 Вычислить определенный интеграл с точностью до 0,001 путем предварительного разложения подынтегральной функции в ряд и почленного интегрирования этого ряда №5 Найти общее решение (общий интеграл) дифференциального уравнения первого порядка Вариант 10 №1. Решить систему трех уравнений с тремя неизвестными методами Крамера и Гаусса: №2 Определить производные
№3 Найти интегралы:а)
№4 Вычислить определенный интеграл с точностью до 0,001 путем предварительного разложения подынтегральной функции в ряд и почленного интегрирования этого ряда №5 Найти общее решение (общий интеграл) дифференциального уравнения первого порядка Вариант 11 №1. Решить систему трех уравнений с тремя неизвестными методами Крамера и Гаусса: №2 Определить производные №3 Найти интегралы:а)
№4 Вычислить определенный интеграл с точностью до 0,001 путем предварительного разложения подынтегральной функции в ряд и почленного интегрирования этого ряда №5 Найти частное решение дифференциального уравнения, удовлетворяющее указанным начальным условиям Вариант 12 №1. Решить систему трех уравнений с тремя неизвестными методами Крамера и Гаусса: №2 Определить производные №3 Найти интегралы:а)
№4 Вычислить определенный интеграл с точностью до 0,001 путем предварительного разложения подынтегральной функции в ряд и почленного интегрирования этого ряда №5 Найти частное решение дифференциального уравнения, удовлетворяющее указанным начальным условиям Вариант 13 №1. Решить систему трех уравнений с тремя неизвестными методами Крамера и Гаусса: №2 Определить производные
№3 Найти интегралы:а)
№4 Вычислить определенный интеграл с точностью до 0,001 путем предварительного разложения подынтегральной функции в ряд и почленного интегрирования этого ряда №5 Найти частное решение дифференциального уравнения, удовлетворяющее указанным начальным условиям Вариант 14 №1. Решить систему трех уравнений с тремя неизвестными методами Крамера и Гаусса: №2 Определить производные
№3 Найти интегралы:а)
№4 Вычислить определенный интеграл с точностью до 0,001 путем предварительного разложения подынтегральной функции в ряд и почленного интегрирования этого ряда №5 Найти частное решение дифференциального уравнения, удовлетворяющее указанным начальным условиям Вариант 15 №1. Решить систему трех уравнений с тремя неизвестными методами Крамера и Гаусса: №2 Определить производные №3 Найти интегралы:а)
№4 Вычислить определенный интеграл с точностью до 0,001 путем предварительного разложения подынтегральной функции в ряд и почленного интегрирования этого ряда №5 Найти частное решение дифференциального уравнения, удовлетворяющее указанным начальным условиям Вариант 16 №1. Решить систему трех уравнений с тремя неизвестными методами Крамера и Гаусса: №2 Определить производные
№3 Найти интегралы:а)
№4 Вычислить определенный интеграл с точностью до 0,001 путем предварительного разложения подынтегральной функции в ряд и почленного интегрирования этого ряда №5 Найти частное решение дифференциального уравнения, удовлетворяющее указанным начальным условиям Вариант 17 №1. Решить систему трех уравнений с тремя неизвестными методами Крамера и Гаусса: №2 Определить производные №3 Найти интегралы:а)
№4 Вычислить определенный интеграл с точностью до 0,001 путем предварительного разложения подынтегральной функции в ряд и почленного интегрирования этого ряда №5 Найти частное решение дифференциального уравнения, удовлетворяющее указанным начальным условиям Вариант 18 №1. Решить систему трех уравнений с тремя неизвестными методами Крамера и Гаусса: №2 Определить производные
№3 Найти интегралы:а)
№4 Вычислить определенный интеграл с точностью до 0,001 путем предварительного разложения подынтегральной функции в ряд и почленного интегрирования этого ряда №5 Найти частное решение дифференциального уравнения, удовлетворяющее указанным начальным условиям Вариант 19 №1. Решить систему трех уравнений с тремя неизвестными методами Крамера и Гаусса: №2 Определить производные
№3 Найти интегралы:а)
№4 Вычислить определенный интеграл с точностью до 0,001 путем предварительного разложения подынтегральной функции в ряд и почленного интегрирования этого ряда №5 Найти частное решение дифференциального уравнения, удовлетворяющее указанным начальным условиям Вариант 20 №1. Решить систему трех уравнений с тремя неизвестными методами Крамера и Гаусса: №2 Определить производные
№3 Найти интегралы:а)
№4 Вычислить определенный интеграл с точностью до 0,001 путем предварительного разложения подынтегральной функции в ряд и почленного интегрирования этого ряда №5 Найти частное решение дифференциального уравнения, удовлетворяющее указанным начальным условиям Вариант 21 №1. Решить систему трех уравнений с тремя неизвестными методами Крамера и Гаусса: №2 Определить производные №3 Найти интегралы:а)
№4 Вычислить определенный интеграл с точностью до 0,001 путем предварительного разложения подынтегральной функции в ряд и почленного интегрирования этого ряда №5 Найти частное решение дифференциального уравнения, удовлетворяющее указанным начальным условиям Вариант 22 №1. Решить систему трех уравнений с тремя неизвестными методами Крамера и Гаусса: №2 Определить производные
№3 Найти интегралы:а)
№4 Вычислить определенный интеграл с точностью до 0,001 путем предварительного разложения подынтегральной функции в ряд и почленного интегрирования этого ряда №5 Найти частное решение дифференциального уравнения, удовлетворяющее указанным начальным условиям Вариант 23 №1. Решить систему трех уравнений с тремя неизвестными методами Крамера и Гаусса: №2 Определить производные
№3 Найти интегралы:а)
№4 Вычислить определенный интеграл с точностью до 0,001 путем предварительного разложения подынтегральной функции в ряд и почленного интегрирования этого ряда №5 Найти частное решение дифференциального уравнения, удовлетворяющее указанным начальным условиям Вариант 24 №1. Решить систему трех уравнений с тремя неизвестными методами Крамера и Гаусса: №2 Определить производные
№3 Найти интегралы: а)
№4 Вычислить определенный интеграл с точностью до 0,001 путем предварительного разложения подынтегральной функции в ряд и почленного интегрирования этого ряда №5 Найти частное решение дифференциального уравнения, удовлетворяющее указанным начальным условиям Вариант 25 №1. Решить систему трех уравнений с тремя неизвестными методами Крамера и Гаусса: №2 Определить производные | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| Поделиться: |
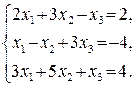
 , пользуясь формулами дифференцирования:
, пользуясь формулами дифференцирования: б)
б)  в)
в)  г)
г)  д)
д) 
 ; б)
; б)  ; в)
; в)  .
.


 б)
б)  в)
в)  г)
г)  д)
д) 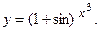
 ; б)
; б)  ; в)
; в)  .
.


 б)
б)  в)
в)  г)
г)  д)
д) 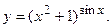
 ; б)
; б)  ; в)
; в) 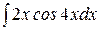 .
.


 б)
б)  в)
в) 
 д)
д) 
 ; б)
; б)  ; в)
; в)  .
.
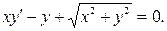

 б)
б)  в)
в)  г)
г)  д)
д) 
 ; б)
; б)  ; в)
; в)  .
.
 .
.
 б)
б)  в)
в)  г)
г)  д)
д) 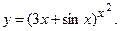
 ; б)
; б)  ; в)
; в)  .
.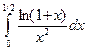


 б)
б)  в)
в) 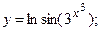 г)
г)  д)
д) 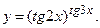
 ; б)
; б)  ; в)
; в)  .
.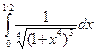


 б)
б)  в)
в)  г)
г)  д)
д) 
 ; б)
; б)  ; в)
; в)  .
.


 б)
б)  в)
в)  г)
г)  д)
д) 
 ; б)
; б)  ; в)
; в)  .
.


 б)
б)  в)
в)  г)
г)  д)
д) 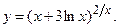
 ; б)
; б)  ; в)
; в)  .
.
 .
.
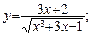 б)
б)  в)
в)  г)
г)  д)
д) 
 ; б)
; б)  ; в)
; в)  .
.
 ,
,  .
.
 б)
б)  в)
в)  г)
г) 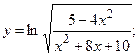 д)
д) 
 ; б)
; б)  ; в)
; в)  .
.
 ,
,  .
.
 б)
б)  в)
в)  г)
г)  д)
д) 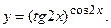
 ; б)
; б)  ; в)
; в) 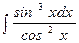 .
.
 ,
, 
 б)
б)  в)
в)  г)
г)  д)
д) 
 ; б)
; б)  ; в)
; в)  .
.
 ,
, 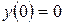 .
.
 б)
б)  в)
в)  г)
г)  д)
д) 
 ; б)
; б)  ; в)
; в)  .
.
 ,
, 
 б)
б)  в)
в)  г)
г)  д)
д)  ; б)
; б)  ; в)
; в)  .
.
 ,
, 

 ; б)
; б)  в)
в)  ; г)
; г)  д)
д) 

 ,
,  .
.
 б)
б)  в)
в)  г)
г)  д)
д) 
 ; б)
; б)  ; в)
; в)  .
.
 ,
,  .
.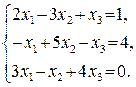
 б)
б)  в)
в)  г)
г)  д)
д) 
 ; б)
; б)  ; в)
; в)  .
.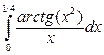
 ,
, 

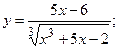 б)
б)  в)
в)  г)
г)  д)
д) 
 ; б)
; б)  ; в)
; в)  .
.
 ,
, 










