
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Риск заболевания шизофренией у родственников больныхСодержание книги
Поиск на нашем сайте
Сопоставление оценок конкордантности МЗ и ДЗ близнецов дает возможность оценить долю влияния наследственных факторов на вариативность исследуемого признака, т.е. коэффициент наследуемости h2. Для этого можно воспользоваться формулой Хольцингера: h2=(СМЗ - СДЗ) / (100 - СДЗ) = (75 - 50) / (100 - 50) = 0,5. Итак, в приведенном примере коэффициент наследуемости (в широком смысле слова) равен 0,5.
Корреляция При анализе количественных признаков сходство между родственниками оценивается с помощью корреляции. Мы уже упоминали об этом, когда обсуждали проблему ассортативности. Сейчас поговорим о корреляциях более подробно. Таблица 6.4 Пример данных для вычисления коэффициента корреляции между ростом и весом
Рассматривая таблицу, мы можем заметить, что отклонение роста каждого человека от средней величины прямо пропорционально таким же отклонениям, относящимся к его весу. В этом примере рост и вес демонстрируют максимальную положительную корреляцию, величина которой равна +1,0. Если мы расположим значения в одном из столбцов в обратном порядке, то получим отрицательную корреляцию с величиной коэффициента, равной -1,0. Если мы в случайном порядке перемешаем все цифры, то корреляция будет близка к 0.
При оценке сходства между родственниками измеряют не два признака у одних и тех же людей, а один и тот же признак в парах родственных индивидов. Ими могут быть близнецы, сибсы, родители и дети и даже неродственники, живущие в одной семье (имеются в виду семьи с приемными детьми) и т.д. Принцип же подсчета корреляций такой же. Важны не абсолютные величины признака, а отклонения от средней. Если отклонения однонаправленны, то и корреляция между родственниками будет высокой (Хрестомат. 6.4).
Итак, в генетике поведения мерой сходства между родственниками чаще всего является корреляция, которая не предполагает сходства в абсолютных величинах признака. Однако нередко в обыденном понимании сходство между родственниками отождествляется со сходством в абсолютных или средних величинах. Такое понимание сходства может приводить к неверной интерпретации получаемых результатов. Таблица 6.5
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-13; просмотров: 199; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.15.111.109 (0.008 с.) |


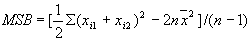 .
.


