
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Практическое занятие № 35-36
Тема занятия «Приложения определенного интеграла» Цель занятия: Показать возможность применения интегрального исчисления к решению задач различных областей естествознания. Организационная форма занятия: семинар-консультация (занятие 35), практикум с применением интерактивной доски (занятие 36). Компетенции, формируемые на занятии: - способность и готовность анализировать социально-значимые проблемы и процессы, использовать на практике методы гуманитарных, естественнонаучных, медико-биологических, и клинических наук в различных видах профессиональной и социальной деятельности (ОК-1); - способностью и готовностью к анализу медицинской информации при помощи системного подхода, к восприятию инноваций в целях совершенствования своей профессиональной деятельности, к использованию полученных теоретических, методических знаний и умений по фундаментальным естественнонаучным, медико-биологическим, клиническим и специальным (в том числе биохимическим) дисциплинам, в научно-исследовательской, лечебно-диагностической, педагогической и других видах работ (ПК-2, частично: формируется способность использовать методы математического анализа в научно-исследовательской деятельности). Формирование у будущих специалистов этих компетенций на занятии предполагает обучение студентов - сформулировать гипотезу и проверить ее в дальнейшем; - анализировать ситуации и делать выводы; - ставить новые вопросы и видеть проблемы в традиционных ситуациях; - абстрагировать содержание и выделять существенное; - применение численных методов решения базовых математических задач в практической деятельности. Вопросы, выносимые на обсуждение 1. Применение определенного интеграла для вычисления площадей. 2. Вычисление длины дуги. 3. Вычисление объемов. 4. Вычисление площади поверхности вращения. 5. Приложения определенного интеграла к решению задач естествознания. Методические рекомендации Для подготовки к занятию дома 1. Прочитайте конспект лекции, соответствующий теме занятия. Запомните основные определения. 2. Изучите рекомендуемую литературу по вопросам, выносимым на обсуждение. 3. Найдите ответы на теоретические задания для развития и контроля владения компетенциями. Подготовьтесь к ответам на эти вопросы на занятии. 4. Законспектируйте ответы на теоретические задания, которые не содержатся в Вашем конспекте лекции по указанной теме. 5. Изучите разобранные примеры решения типовых задач и законспектируйте их решение в рабочую тетрадь. На занятии по указанию преподавателя 1. Дайте ответы на вопросы из теоретических заданий для развития и контроля владения компетенциями. 2. В рабочей тетради и на доске решите практические задания для развития и контроля владения компетенциями из заданий, решаемых в аудитории. 3. Разберите с преподавателем вопросы, которые остались Вами не понятыми по теме этого занятия. 4. На занятии 36 решите предложенный вариант самостоятельной работы№12 по теме «Определенный интеграл» и сдайте на проверку преподавателю. Дома 1. Закрепите полученные практические умения и навыки, решая практические задания для развития и контроля владения компетенциями из заданий для самостоятельной работы дома. К занятию 36 закончите выполнение ИДЗ №7 по теме «Основные методы интегрирования. Приложения определенного интеграла» и сдайте на проверку преподавателю. 2. Подготовьтесь к итоговому компьютерному тестированию по разделу «Интегральное исчисление функции одной переменной. Рекомендуемая литература [1] глава 9 пп 9.10 - 9.11. [2] глава X §§ 3 – 9. [3] глава 8 §§ 45 – 46. [4] часть III занятия 15 – 16. [5] глава 5 § 5.6. [6] глава 8 § 10. [7] глава VIII §10. [8] глава 6 § 11. ПРИМЕРЫ РЕШЕНИЯ ТИПОВЫХ ЗАДАЧ 1. Вычислите площадь, ограниченную параболами
Решение. Определим точки пересечения парабол и построим эти параболы: Ординаты точек пересечения находим, подставляя найденные абсциссы в уравнение одной из парабол:
Из рисунка видим, что площадь искомой фигуры
Площадь ОВD расположена под осью
Отсюда
2. Найдите площадь одного лепестка кривой Решение. Один лепесток кривой получаем при изменении
Применяя формулы тригонометрии, имеем:
Отсюда
3. Найдите объем тела, образованного вращением фигуры, ограниченной одной полуволной синусоиды
Решение. Объем тела вращения, образованного вращением кривой вокруг оси
4. Найти объем тела, полученного вращением вокруг оси Решение. Объем тела вращения, образованного вращением кривой вокруг осии
Пользуясь данными параметрическими уравнениями циклоиды, преобразуем интеграл к переменной
Тогда
5. Найдите длину дуги полукубической параболы
Решение. Для вычисления длины дуги в прямоугольной декартовой системе координат воспользуемся формулой: Разрешим данное уравнение кривой относительно
(Знаки Тогда
6. Найдите длину астроиды Решение. Длина дуги кривой, заданной параметрически, вычисляется по формуле:
Найдем Учитывая симметричность астроиды, найдем длину ее дуги при изменении
7. Скорость роста некоторой популяции микроорганизмов подчинена закону Решение. Так как скорость роста популяции
Тогда
Теоретические задания
|
||||
|
Последнее изменение этой страницы: 2016-12-09; просмотров: 328; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.12.73.149 (0.007 с.) |
 и
и 
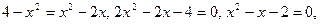 отсюда,
отсюда,  - абсциссы точек пересечения.
- абсциссы точек пересечения.
 и
и  - точки пересечения парабол.
- точки пересечения парабол.

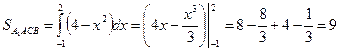

 , поэтому перед знаком интеграла берем знак «минус».
, поэтому перед знаком интеграла берем знак «минус».


 от 0 до
от 0 до  . По формуле вычисления площади в полярных координатах имеем
. По формуле вычисления площади в полярных координатах имеем



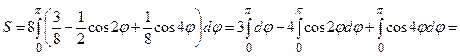

 , прямой
, прямой  вокруг оси
вокруг оси 


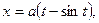
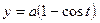

 тогда
тогда  при
при  при
при 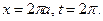


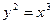 от начала координат до точки
от начала координат до точки 


 и находим
и находим 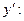
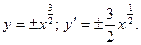
 в выражении
в выражении 


 где
где  .
. и
и 
 от 0 до
от 0 до  (длина дуги, расположенной в 1 четверти). Тогда длина всей дуги
(длина дуги, расположенной в 1 четверти). Тогда длина всей дуги

 где
где  , если численность этой популяции в момент времени 30с была 100000 единиц.
, если численность этой популяции в момент времени 30с была 100000 единиц. является производной от численности популяции
является производной от численности популяции  , следовательно, численность популяции
, следовательно, численность популяции  или
или 





