Графическое представление результатов

 

В большинстве лабораторных работ связь между физическими величинами необходимо представить на графике. При построении графиков следует руководствоваться следующими правилами:

График нужно выполнить на миллиметровой бумаге используя, как правило, прямоугольную систему координат.

При выборе масштаба необходимо учитывать следующее:

1) цена наименьшего деления на координатных осях не должна превышать абсолютной ошибки физической величины;

2) для каждой координатной оси необходимо указывать масштаб и единицу измерения;

3) единицы измерения физических величин должны соответствовать международной системе единиц (СИ), а используемый масштаб должен быть удобным;

4) пересечение координатных осей необязательно должно совпадать с нулевыми значениями физических величин.

При выборе начала координат надо стремиться к тому, чтобы поле графика использовалось полностью.

Наносимые на график точки необходимо изображать четко и ясно. Каждую точку обводят кружочком или через нее проводят крестик, полуразмер которого равен абсолютной ошибке величин откладываемых вдоль координатных осей.

Через экспериментальные точки проводят плавную кривую. При этом следят за тем, чтобы точки отстояли от этой кривой не более чем на половину ошибки. Число точек, лежащих выше и ниже кривой должно быть примерно одинаковым.

График часто строят в переменных, которые приводят к линейной зависимости величин.

ЛАБОРАТОРНАЯ РАБОТА

Изучение механических колебаний

Движение, повторяющееся через отдельные промежутки времени, называется колебательным. В живом организме и при диагностике и лечении заболеваний очень широко распространены процессы с повторением различных состояний и описывающих их параметров.

 

ЦЕЛЬ занятия:

1. Ознакомиться с характеристиками колебаний.

2. Изучить сложение гармонических колебаний и явление резонанса.

Исходные знания:

1. Знать виды механических колебаний.

 

План изучения темы:

1.Свободные механические колебания (незатухающие и затухающие).

2. Кинетическая и потенциальная энергии колебательного движения.

3. Сложение гармонических колебаний.

4. Сложное колебание и его гармонический спектр.

5. Вынужденные колебания. Резонанс.

6. Автоколебания.

ЛИТЕРАТУРА:

1. Лекции.

2. А.Н. Ремизов. Медицинская и биологическая физика, М., 2004, гл. 5, с.71-87.

3. Н.М. Ливенцев Курс физики, М., 1978, т.1, гл.4. с. 67-81.

4. М.Е. Блохина, И.А. Эссаулова, Г.В. Мансурова. Руководство к лаб. работам по медицинской и биологической физике, М., 2001, с. 44-52.

 

ТЕОРЕТИЧЕСКие предпосылки работы:

Многие процессы в организме являются периодическими, и их можно рассматривать как колебательные, например, процесс дыхания, работа сердца, электрические процессы в сердце и т.д. Рассмотрим механические колебания материальной точки массой m. Примером такой колебательной системы служит пружинный маятник. По второму закону Ньютона

(1)

Предположим, что в данном случае силой трения можно пренебречь, тогда колебания будут происходить под действием упругой силы F = -kx. Тогда соотношение (1) принимает вид:

(2)

Заменяя , получаем дифференциальное уравнение гармонических колебаний

(3)

Его решение имеет вид:

(4)

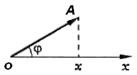
где ω₀ – круговая частота колебаний,

А - амплитуда, (ω₀t + φ₀)— фаза колебаний,

φ₀ - начальная фаза,

x - смещение колеблющейся точки относительно положения равновесия.

График зависимости х = f(t) изображен на рис. 1. Гармонические колебания можно изображать в виде векторных диаграмм (рис. 2). Из точки О, взятой на оси ОХ, проводят вектор А, модуль которого равен амплитуде колебаний.

 

Рис. 1. Рис.2.

Угол φ представляет собой фазу колебаний, а проекция вектора А на ось OX – смещение колеблющейся точки.

Материальная точка может одновременно участвовать в нескольких колебательных движениях. При сложении двух гармонических колебаний, направленных по одной прямой, получается более сложное колебательное движение. Пусть материальная точка участвует в двух гармонических колебаниях одного направления и с одинаковой круговой частотой ω₀:

Тогда результирующее смещение х точки равно алгебраической сумме обоих смещений:

x = x₁+ x₂, (5)

а результирующее движение представляет собой периодическое колебательное движение с той же частотой.

Амплитуда А результирующего колебания равна

(6)

Начальную фазу φ₀ результирующего колебания можно вычислить по формуле

(7)

Если частоты складываемых колебаний неодинаковы, то результирующее движение будет негармоническим. При сложении двух гармонических колебаний, совершающихся во взаимно перпендикулярных направлениях, получаются различные траектории материальной точки, называемые фигурами Лиссажу. Форма этих фигур зависит от соотношения частот, фаз и амплитуд складываемых колебаний.

Свободные колебания реальных систем всегда затухают. Затухание свободных механических колебаний вызывается главным образом трением. Д ифференциальное уравнение затухающих колебаний имеет вид:

(8)

где (ω₀ – круговая частота собственных колебаний системы (k/m = ); β — коэффициент затухания. Если > β², то решение этого уравнения имеет вид:

(9)

где ω_{0 –} круговая частота затухающих колебаний ω²=(), A₀ – начальная амплитуда, φ₀ – начальная фаза. График зависимости x = f(t) изображеннарисунке 3.

Если > β², то колебаний нет и движение будет апериодическим .

 

Рис.3.

Кроме коэффициента затухания, для характеристики затухающих колебаний используют логарифмический декремент затухания λ. Он определяется как натуральный логарифм отношения двух последовательных амплитуд, соответствующих моментам времени, отличающимсянапериод:

(10)

Колебания тела, вызванные и поддерживаемые внешней силой, периодически изменяющейся по величине и направлению, называются вынужденными колебаниями, а внешняя сила – вынуждающей силой. Пусть вынуждающая сила изменяется по закону

F = F₀cosωt,

(11)

где f₀ — максимальное значение силы, ω — круговая частота. Тогда дифференциальное уравнение вынужденных колебаний принимает вид:

( 12 )

Решение этого уравнения представляет собой сумму уравнений, описывающих свободные и вынужденные колебания.

Свободные колебания довольно быстро затухают. Поэтому, пренебрегая собственными колебаниями системы, решение уравнения (12) записывают в следующем виде:

x= А соs (ωt + φ₀). ( 13)

Таким образом, под действием периодической внешней силы ( 11 ) возникаютвынужденные гармонические колебания с частотой, равной частоте вынуждающей силы.

В этом случае, если частота ω вынуждающей силы принимает значение ω_рез, амплитуда вынужденных колебаний системы достигает максимального значения. Это явление называется резонансом. Частота ω_рез называется резонансной частотой:

(14)

Амплитуда колебаний А_рез, определяется по формуле

(15)

 

ВОПРОСЫ ДЛЯ САМОКОНТРОЛЯ:

1. Что такое колебательное движение?

2. Какие виды колебаний различают?

3. Какие колебания называются гармоническими?

4. Что называется смещением? амплитудой? периодом? частотой? фазой колебаний?

5. Запишите дифференциальное уравнение гармонического колебания.

6. Запишите уравнения смещения, скорости и ускорения при гармоническом колебании.

7. В чем заключается метод векторных диаграмм?

8. Опишите процесс сложения гармонических колебаний, направленных по одной прямой и во взаимно перпендикулярных направлениях.

9. Запишите дифференциальное уравнение затухающего колебания.

10. Запишите уравнение смещения для затухающего колебания.

11. Как зависит амплитуда затухающих колебаний от времени?

12. Что такое коэффициент затухания и логарифмический декремент затухания?

13. Какие колебания называются сложными? Что такое гармонический спектр сложного колебания?

14. Какие колебания называют вынужденными? Запишите уравнение смещения для вынужденного колебания.

15. В чем заключается явление резонанса при вынужденных колебаниях?

16. Какие колебания называют автоколебаниями?

Приборы и принадлежности:

Персональный компьютер.

Схема работы:

Последовательность действий	Способ выполнения задания
1. Определение по графику характеристик гармонических колебаний	1. Получите на экране график гармонических колебаний маятника и зарисуйте в тетрадь 2. Определите по графику амплитуду А и период Т колебаний (см. рис. 1) 3. Измените амплитуду колебаний в k1 раз, а период в k2 раз 4. Повторите действия п. 1 и 2 5. Полученные результаты занесите в таблицу 1 6. Определите по графику начальную фазу колебаний φ0 и укажите, каким способом маятник был приведен в движение. Таблица №1
Параметр	Исходный график	Измененный график	Коэффициент
А,м			k1
Т,с			k2
2. Изучение векторных диаграмм.	1. Определите по приведенной векторной диаграмме амплитуду и начальную фазу колебаний 2. Получите на экране графики временной зависимости смещения х = f(t), скорости υ = f(t) и ускорения а = f(t) ко леблющегося тела и укажите соответствующие им векторные диаграммы.
3. Изучение сложения колебаний, происходящих вдоль одной прямой	1. Изобразите в тетради полученную на экране векторную диаграмму сложения двух колебаний одинаковой частоты и определите по ней амплитуду и начальную фазу результирующего колебания 2. Получите на экране график результирующего колебания, полученного при сложении двух гармонических колебаний с частотами ν1 и ν2 и амплитудами А1 и А2. Постройте его гармонический спектр 3. Полученные графики перенесите в тетрадь 4. Получите на экране график результирующего колебания, полученного при сложении четырех заданных гармонических колебаний различных частот. Амплитуды и периоды складываемых колебаний занесите в таблицу №.2. Таблица №2
Колебание	Амплитуда колебания	Период колебания
4. Изучение сложения взаимно перпендикулярных колебаний	1. Задавая амплитуды, круговые частоты и начальные фазы взаимно перпендикулярных колебаний х = f(t) и у = f(t), получите на экране фигуры Лиссажу, образующиеся при сложении данных колебаний 2. Опыт 1. повторите три раза. Полученные фигуры и уравнения складываемых колебаний занесите в тетрадь
5. Изучение затухающих колебаний	1. Получите на экране график затухающих колебаний и зарисуйте его в тетрадь 2. Определите по графику логарифмический декремент затухания λ, и коэффициент затухания β [см. формулу (10)].
Последовательность действий	Способ выполнения задания
6. Изучение резонансных кривых вынужденных колебаний	1. Задавая параметры колебательной системы (т, k, β) и амплитуду вынуждающей силы f0, вычислите собственную круговую частоту колебаний ω0 и резонансную частоту ωрез вынужденных колебаний [см. формулу (14)] 2. Получите на экране изображение резонансной кривой 3. Изменяя значение β, пронаблюдайте изменения вида резонансных кривых. Значения β занесите в таблицу 3. Таблица №3
β1	β2	βисх	β3	β4

ЛАБОРАТОРНАЯ РАБОТА

 

Изучение работы аппарата для ультразвуковой терапии

 

Аппараты, генерирующие ультразвуковые колебания, используются в медицине для лечения ряда заболеваний периферической нервной системы, опорно-двигательного аппарата и др., а также с диагностической целью.

 

ЦЕЛЬ занятия:

1. Ознакомиться с устройством и принципом работы аппарата для ультразвуковой терапии.

2. Определить особенности воздействия ультразвука (тепловой эффект) на различные вещества (электролиты и диэлектрики) при разнообразных режимах генерации УЗ аппаратом для ультразвуковой терапии УЗТ-1.01.Ф.

ИСХОДНЫе ЗНАНИя:

1. Знать физические характеристики механических волн.

 

ПЛАН ИЗУЧЕНИЯ ТЕМЫ:

1. Характеристики УЗ-волн.

2. Свойства УЗ-волн.

3. Способы получения УЗ-волн.

4. Источники УЗ-волн.

5. Воздействие УЗ на биологические объекты.

6. Диагностическое и терапевтическое применение УЗ в медицине.

 

ЛИТЕРАТУРА:

1. Лекции.

2. А.Н. Ремизов. Медицинская и биологическая физика, М., 2004, гл. 6, с. 108 - 111.

3. Н.М. Ливенцев Курс физики, М., 1978, т.1, гл.5. с. 103 - 106.

4. М.Е. Блохина, И.А. Эссаулова, Г.В. Мансурова. Руководство к лаб. работам по медицинской и биологической физике, М., 2001, с. 57-62.