
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Применения первого начала термодинамики к изопроцессам.Содержание книги
Поиск на нашем сайте
Адиабатический процесс — термодинамический процесс в макроскопической системе, при котором система не получает и не отдаёт тепловой энергии. Серьёзное исследование адиабатических процессов началось с XVIII века. Адиабатический процесс является частным случаем политропного процесса. Адиабатические процессы обратимы, если их проводить достаточно медленно (квазистатически). В общем случае адиабатический процесс необратим.Некоторые авторы (в частности, Л. Д. Ландау) называли адиабатическими только квазистатические адиабатические процессы. Адиабатический процесс для идеального газа описывается уравнением Пуассона. Для адиабатического процесса первое начало термодинамики в силу отсутствия теплообмена (Δ Q = 0) системы со средой имеет вид
где: § § §
где Энтропия системы в обратимом адиабатическом процессе не меняется[6]:
|
|||||||||
|
Последнее изменение этой страницы: 2016-12-12; просмотров: 293; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.152.49 (0.009 с.) |

 Из первого начала термодинамики (δQ=dU+δA) для изохорного процесса следует, что вся теплота, которая сообщается газу, идет на увеличение его внутренней энергии:
Из первого начала термодинамики (δQ=dU+δA) для изохорного процесса следует, что вся теплота, которая сообщается газу, идет на увеличение его внутренней энергии:  т.к. CV=dUm/dt,
т.к. CV=dUm/dt,  (1) Изобарный процесс (p=const). Диаграмма этого процесса (изобара) в координатах р, V изображается прямой, которая параллельна оси V. При изобарном процессе работа газа при увеличения объема от V1 до V2 равна
(1) Изобарный процесс (p=const). Диаграмма этого процесса (изобара) в координатах р, V изображается прямой, которая параллельна оси V. При изобарном процессе работа газа при увеличения объема от V1 до V2 равна  откуда
откуда  Тогда выражение (2) для работы изобарного расширения примет вид
Тогда выражение (2) для работы изобарного расширения примет вид  (3) Из этого выражения вытекает физический смысл молярной газовой постоянной R: если T2 —T1 = 1К, то для 1 моль газа R=A, т. е. R численно равна работе изобарного расширения 1 моль идеального газа при нагревании его на 1 К.
(3) Из этого выражения вытекает физический смысл молярной газовой постоянной R: если T2 —T1 = 1К, то для 1 моль газа R=A, т. е. R численно равна работе изобарного расширения 1 моль идеального газа при нагревании его на 1 К.
 Рис.1
В изобарном процессе при сообщении газу массой m количества теплоты
Рис.1
В изобарном процессе при сообщении газу массой m количества теплоты  его внутренняя энергия возрастает на величину (т.к. CV=dUm/dt)
его внутренняя энергия возрастает на величину (т.к. CV=dUm/dt)  При этом газ совершит работу, определяемую выражением (3). Изотермический процесс (T=const). Изотермический процесс описывается законом Бойля—Мариотта:
При этом газ совершит работу, определяемую выражением (3). Изотермический процесс (T=const). Изотермический процесс описывается законом Бойля—Мариотта:  Так как при Т=const внутренняя энергия идеального газа не изменяется:
Так как при Т=const внутренняя энергия идеального газа не изменяется:  то из первого начала термодинамики (δQ=dU+δA) следует, что для изотермического процесса
то из первого начала термодинамики (δQ=dU+δA) следует, что для изотермического процесса  т. е. все количество теплоты, сообщаемое газу, расходуется на совершение им работы против внешних сил:
т. е. все количество теплоты, сообщаемое газу, расходуется на совершение им работы против внешних сил:  (4) Значит, для того чтобы при расширении газа температура не становилась меньше, к газу в течение изотермического процесса необходимо подводить количество теплоты, равное внешней работе расширения.
(4) Значит, для того чтобы при расширении газа температура не становилась меньше, к газу в течение изотермического процесса необходимо подводить количество теплоты, равное внешней работе расширения.
 Линия, изображающая адиабатный процесс на какой-либо термодинамической диаграмме, называется адиабатой. Существует ряд явлений природы, которые могут считаться адиабатическим процессом, кроме того, он получил применение в технике.
Линия, изображающая адиабатный процесс на какой-либо термодинамической диаграмме, называется адиабатой. Существует ряд явлений природы, которые могут считаться адиабатическим процессом, кроме того, он получил применение в технике. 
 — изменение внутренней энергии тела,
— изменение внутренней энергии тела,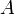 — работа, совершаемая системой
— работа, совершаемая системой — теплота, полученная системой
— теплота, полученная системой ,
, — дифференциальное выражение для работы, ai — внешние параметры, Ai — соответствующие им внутренние параметры.
— дифференциальное выражение для работы, ai — внешние параметры, Ai — соответствующие им внутренние параметры. .
.


