Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вивчення законів деформації та визначення модуля Юнга
Вивчення законів деформації та визначення модуля Юнга Мета роботи
Вивчення пружної деформації та закону, який його описує; визначення коефіцієнта жорсткості і модуля Юнга. Теоретична частина Залежно від напрямку і величини сил, які прикладені до твердого тіла, існують такі види деформації: розтягнення, стиснення, згинання, кручення. Деформації бувають пружні і пластичні. При пружній деформації виконується закон Гука: в області пружних деформацій сила пружності пропорційна абсолютній деформації: Fy = –kx, (2 1) де коефіцієнт k називають коефіцієнтом пружності. Під час розтягнення або стиснення стрижнів закон Гука записують через відносну деформацію
де Е – модуль Юнга (модуль пружності першого роду). Якщо Реальна залежність механічної напруги від деформації під час розтягнення стрижнів представлена на рис. 2.2. На графіку залежності
Рис. 2.1 Рис. 2.2
Скориставшись графіком залежності
Механічну напругу знайдемо за формулою:
де m – маса важеля. Перевірка другого закону Ньютона Мета роботи
Перевірка другого закону Ньютона за допомогою установки Атвуда. Теоретична частина
В роботі вивчають поступальний рух системи вантажів 2 і 3
(рис. 3.1), які закріплені на легкій нитці, яка перекинута через нерухомий блок. Система вантажів дає змогу рухатися під дією сили тяжіння перевантаження масою
Рис. 3.1
За другим законом Ньютона добуток маси на прискорення дорівнює сумі сил, які діють на вантажі. Рівняння руху вантажів у скалярній формі:
Під час перевіркі другого закону Ньютона, тобто залежності прискорення від діючої сили, необхідно, щоб маса залишалася постійною, а змінювалася тільки сила Таким чином, в цій роботі потрібно перевірити, що прискорення пропорційно діючій силі:
Якщо під час вимірювань пройдений вантажами шлях
З формули 3.4 випливає, що відношення прискорень пропорційне відношенню квадратів відрізків часу:
На приладі Атвуда Мета роботи
Вивчення поступального руху за допомогою приладу Атвуда і визначення прискорення вільного падіння. Теоретична частина
В роботі вивчається поступальний рух вантажів 2 і 3, які закріплені на легкій нитці, що перекинута через нерухомий блок 1 (рис. 4.1). Система вантажів дає змогу рухатися під дією сили тяжіння перевантаження масою Рис. 4.1 Рис.4.2 На вантажі діють сили тяжіння
Розв’язавши сумісно рівняння руху стосовно прискорення, отримаємо:
Якщо після проходження деякого шляху S1 (від платформи 4 до платформи 5) зняти перевантаження за допомогою платформи 5 (рис.4.2), то далі рух на відрізку шляху S (від платформи 5 до 7) буде рівномірним (при малій силі тертя) зі швидкістю
Час проходження відрізка шляху S знайдемо за формулою:
Прискорення вільного падіння знайдемо за формулою 4.3, підставивши значення прискорення
Мета роботи
Перевірка основного закону динаміки обертального руху івизначення моменту інерції за допомогою установки Обербека. Теоретична частина
 . Рівняння руху вантажу m: . Рівняння руху вантажу m:
де Модуль моменту сили, який діє на шків і приводить в рух обертальну частину установки:
де r – радіус шківа,
З формул 5.2 і 5.3 можна дістати формулу для визначення моменту сили:
З іншого боку за основним законом динаміки обертального руху:
Праві частини формул 4.4 і 4.5 рівні, тому:
З формули 5.6 для розрахунку моменту інерції хрестовини маємо:
Момент інерції вантажу mi відносно осі обертання:
Мета роботи
Вивчення прискореного руху системи вантажів і визначення динамічних характеристик (сили тертя і моменту сили тертя). Теоретична частина
В роботі вивчають прискорений рух вантажів, які закріплені на легкій нитці, яка перекинута через нерухомий блок. Система вантажів починає рухатися під дією сил тяжіння перевантаження масою m1. Фізичну модель досліду можна представити у вигляді схеми, зображеної на рис. 6.1.
а такожмоментефективноїсили тертя Мтер. Складемо математичну модель досліду. За другим законом Ньютона, добуток маси на прискорення дорівнює сумі сил, які діють на вантажі: Рис. 6.1
Рівняння моментів сил для блоку, який обертається навколо нерухомої осі:
де I – момент інерції блока (момент інерції характеризує інерцію тіл під час обертального руху),
Сили натягу ниток рівні за модулем і
Прискорення системи З формули 6.5 видно, що якщо прискорення системи вантажів дорівнює нулю
Формула 6.6 свідчить, що силу тертя можна знайти, якщо екстраполювати графік залежності прискорення від сил тяжіння перевантажень до перетину з віссю абсцис.
Прискорення вантажів можна обчислити за формулою:
де h – пройдена вантажами відстань, t – час руху.
Лабораторна установка показана на рис. 6.2. Через легкий блок перекинута нитка з вантажами. Якщо на правий вантаж покласти невелике переван-таження Рi = mig, то система вантажів почне рухатися з прискоренням, у момент удару вантажу по нижній платформі спрацює вимикач секундоміра. Під час виконання роботи потрібно: 1) встановити нижню платформу з автоматичним вимикачем на відстані h = 0,6 – 0,8 м; Рис. 6.2 2) підняти правий вантаж з невеликим перевантаженням до нульової відмітки; 3) відпустити правий вантаж, водночас включивши секундомір; 4) виміряти час руху вантажу з перевантаженням три рази і знайти середнє значення; 5) додаючи до вантажу додаткові перевантаження (2 – 8 г.) викона-ти пп.2 – 4, а дані внести у табл. 6.1.
Таблиця 6.1
Вивчення законів деформації та визначення модуля Юнга Мета роботи
Вивчення пружної деформації та закону, який його описує; визначення коефіцієнта жорсткості і модуля Юнга. Теоретична частина Залежно від напрямку і величини сил, які прикладені до твердого тіла, існують такі види деформації: розтягнення, стиснення, згинання, кручення. Деформації бувають пружні і пластичні. При пружній деформації виконується закон Гука: в області пружних деформацій сила пружності пропорційна абсолютній деформації: Fy = –kx, (2 1) де коефіцієнт k називають коефіцієнтом пружності. Під час розтягнення або стиснення стрижнів закон Гука записують через відносну деформацію
де Е – модуль Юнга (модуль пружності першого роду). Якщо Реальна залежність механічної напруги від деформації під час розтягнення стрижнів представлена на рис. 2.2. На графіку залежності
Рис. 2.1 Рис. 2.2
Скориставшись графіком залежності
Механічну напругу знайдемо за формулою:
де m – маса важеля.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-12; просмотров: 215; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.179.238 (0.012 с.) |
 і механічну напругу
і механічну напругу  . У формулі для
. У формулі для 
 абсолютна деформація,,
абсолютна деформація,,  початкова,
початкова,  кінцева довжина стрижня,
кінцева довжина стрижня,  – механічна напруга відношення зовнішньої сили, яка прикладена перпендикулярно перерізу стрижня до площі перерізу (рис. 2.1). В цьому разі закон Гука формулюється так: в області пружної деформації відносна деформація прямо пропорційна механічній напрузі:
– механічна напруга відношення зовнішньої сили, яка прикладена перпендикулярно перерізу стрижня до площі перерізу (рис. 2.1). В цьому разі закон Гука формулюється так: в області пружної деформації відносна деформація прямо пропорційна механічній напрузі: (2.2)
(2.2) , тобто
, тобто  , то
, то  тобто модуль Юнга дорівнює механічній напрузі, яку потрібно прикласти до тіла, щоб збільшити його довжину вдвічі.
тобто модуль Юнга дорівнює механічній напрузі, яку потрібно прикласти до тіла, щоб збільшити його довжину вдвічі. є три області. Перша – 0–1 – область пружності характеризується лінійною залежністю механічної напруги від деформації. Друга область – 0–2 – це область пластичної деформації. Далі, до руйнування у точці 3, іде область зміцнення. Якщо стрижень деформувати до точки 2, то під час зменшення напруги графік не піде через точку 1 і стрижень не повернеться до початкового стану – спостерігається залишкова (пластична) деформація.
є три області. Перша – 0–1 – область пружності характеризується лінійною залежністю механічної напруги від деформації. Друга область – 0–2 – це область пластичної деформації. Далі, до руйнування у точці 3, іде область зміцнення. Якщо стрижень деформувати до точки 2, то під час зменшення напруги графік не піде через точку 1 і стрижень не повернеться до початкового стану – спостерігається залишкова (пластична) деформація.
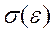 в області пружної деформації 0-1, можна знайти модуль Юнга за формулою:
в області пружної деформації 0-1, можна знайти модуль Юнга за формулою: (2.3)
(2.3) (2.4)
(2.4)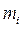 . Фізичну модель досліду можна представити у вигляді схеми, зображеної на рис. 3.1. На вантажі діють сили тяжіння
. Фізичну модель досліду можна представити у вигляді схеми, зображеної на рис. 3.1. На вантажі діють сили тяжіння  та
та  і сили натягу ниток
і сили натягу ниток  і
і  . Якщопід час обертання блока навколо осі не враховувати сили тертя, то
. Якщопід час обертання блока навколо осі не враховувати сили тертя, то 

 ; (3.1)
; (3.1) (3.2)
(3.2) Це можна здійснити, якщо покласти на лівий і правий вантажі декілька перевантажень і перекладати їх з одного вантажу на другий так, щоб загальна маса оставалася незмінною, а сила
Це можна здійснити, якщо покласти на лівий і правий вантажі декілька перевантажень і перекладати їх з одного вантажу на другий так, щоб загальна маса оставалася незмінною, а сила  яка рухає систему вантажів, змінювалася.
яка рухає систему вантажів, змінювалася. (3.3)
(3.3)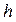 лишається незмінним, то виконується співвідношення:
лишається незмінним, то виконується співвідношення: (3.4)
(3.4)
 (3.5)
(3.5)
 (4.1)
(4.1) (4.3)
(4.3)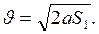 (4.4)
(4.4) (4.5)
(4.5) і
і  з формул 4.4 і 4.5:
з формул 4.4 і 4.5:
 (4.6)
(4.6) (5.1)
(5.1) – сила тяжіння вантажу,
– сила тяжіння вантажу, 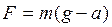 – сила натягу шнура, на якому закріплений вантаж m. За третім законом Ньютона сила, яка діє на шків, дорівнює силі натягу шнура –
– сила натягу шнура, на якому закріплений вантаж m. За третім законом Ньютона сила, яка діє на шків, дорівнює силі натягу шнура – 
 (5.2)
(5.2) – прискорення вантажу m. Тангенціальне прискорення точок на поверхні шківа те ж саме, що і прискорення вантажу m, тобто
– прискорення вантажу m. Тангенціальне прискорення точок на поверхні шківа те ж саме, що і прискорення вантажу m, тобто 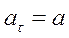 . Спостерігаючи за падінням вантажу m, можна визначити прискорення за формулою:
. Спостерігаючи за падінням вантажу m, можна визначити прискорення за формулою: (5.3)
(5.3) (5.4)
(5.4) (5.5)
(5.5) (5.6)
(5.6)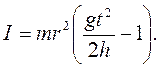 (5.7)
(5.7) (5.8)
(5.8) На вантажі діють сили тяжіння mg та (m+m1)g і сили натягу ниток T1 і T2. Під час обертання блока навколо осі з тертям необхідно враховувати моменти сил М1 = RT1sin900 i М2 = RT2sin900,
На вантажі діють сили тяжіння mg та (m+m1)g і сили натягу ниток T1 і T2. Під час обертання блока навколо осі з тертям необхідно враховувати моменти сил М1 = RT1sin900 i М2 = RT2sin900,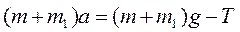 ; (6.1)
; (6.1) (6.2)
(6.2) (6.3)
(6.3) . (6.4)
. (6.4) . Розв’язавши систему рівнянь: 6.1 – 6.4 отримаємо формулу для прискорення системи вантажів:
. Розв’язавши систему рівнянь: 6.1 – 6.4 отримаємо формулу для прискорення системи вантажів: (6.5)
(6.5) і вантажів неможливо обчислити за формулою 6.5, тому що сила тертя і момент інерції блока невідомі. Але, якщо маса перевантаження
і вантажів неможливо обчислити за формулою 6.5, тому що сила тертя і момент інерції блока невідомі. Але, якщо маса перевантаження  <
<  його масою можна знехтувати, тоді можна вважати, що прискорення системи лінійно залежить від сили тяжіння перевантаження mig.
його масою можна знехтувати, тоді можна вважати, що прискорення системи лінійно залежить від сили тяжіння перевантаження mig. то вага перевантаження дорівнює силі тертя:
то вага перевантаження дорівнює силі тертя: (6.6)
(6.6) , (6.7)
, (6.7) 6.3. Експериментальні дослідження
6.3. Експериментальні дослідження