
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Оценка тесноты линейной связиСодержание книги
Поиск на нашем сайте
Пример. Имеются данные по восьми однотипным фирмам о часовой оплате труда х и уровне текучести кадров у:
Требуется: 1) найти уравнение регрессии 2) измерить тесноту связи между признаками х и у. Решение. Для решения задачи построим вспомогательную таблицу (табл. 10.4). Таблица 10.4 Расчетная таблица для определения линейного коэффициента корреляции
1) Применяя метод приведения параллельных данных, видим, что с ростом значений признака х, значения признака у убывают. Поэтому с помощью графика зависимости у = у (х) можно предположить, что зависимость между х и у обратная, линейная. Для построения линейного уравнения регрессии
Подставляя в это уравнение последовательно значения х =30, 40, 50 и т.д., получаем выровненные (теоретические) значения результативного показателя Выровненные уровни 2) Для измерения тесноты связи межу х и у применим формулу линейного коэффициента корреляции rху, т.к. связь линейная и число признаков равно двум. 2.1. Линейный коэффициент корреляции:
2.2. Воспользуемся еще одной формулой линейного коэффициента корреляции:
Таким образом, между оплатой труда х и уровнем текучести кадров у существует сильная обратная связь, т.е. с увеличением оплаты труда текучесть кадров снижается. Теснота связи при нелинейной зависимости измеряется с помощью корреляционного отношения. Различают эмпирическое и теоретическое корреляционное отношение. Эмпирическое корреляционное отношение рассчитывается по формуле:
где
Теоретическое корреляционное отношение рассчитывается по формуле:
где
В данном виде корреляционное отношение при криволинейной зависимости обычно называют индексом корреляции. Корреляционное отношение С помощью корреляционного отношения Таблица 10.4
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-10; просмотров: 364; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.152.49 (0.006 с.) |

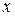 )
)
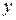 )
)
 (уравнение зависимости уровня текучести кадров от величины часовой оплаты труда);
(уравнение зависимости уровня текучести кадров от величины часовой оплаты труда);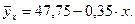
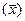




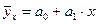 найдем параметры а 0 и а 1:
найдем параметры а 0 и а 1: =
=  - коэффициент регрессии, показывает, на сколько (в абсолютном выражении) изменяется значение результативного признака у при изменении факторного признака х на единицу.
- коэффициент регрессии, показывает, на сколько (в абсолютном выражении) изменяется значение результативного признака у при изменении факторного признака х на единицу. уравнение регрессии
уравнение регрессии 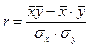 .
.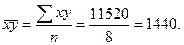

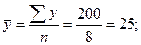
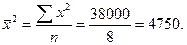
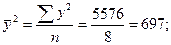
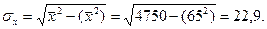
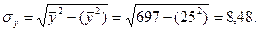
 связь обратная сильная, т.к.
связь обратная сильная, т.к. 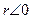 и
и 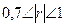 .
.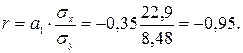
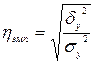 ,
,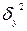 - межгрупповая дисперсия результативного признака, определяемая по формуле
- межгрупповая дисперсия результативного признака, определяемая по формуле 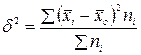 ;
; - общая дисперсия результативного признака, определяемая по формуле
- общая дисперсия результативного признака, определяемая по формуле 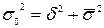 .
.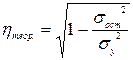 ,
,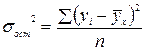 - остаточная дисперсия, отражающая вариацию результативного признака за счет факторов, не учтенных в уравнении регрессии. Значит, общая дисперсия эмпирического ряда
- остаточная дисперсия, отражающая вариацию результативного признака за счет факторов, не учтенных в уравнении регрессии. Значит, общая дисперсия эмпирического ряда 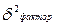 +
+  .
.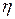 показывает только силу связи и изменяется в пределах от 0 до 1
показывает только силу связи и изменяется в пределах от 0 до 1 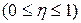 . Направление связи определяют по групповым и корреляционным таблицам. Корреляционное отношение применимо для парной и множественной корреляции независимо от формы связи.
. Направление связи определяют по групповым и корреляционным таблицам. Корреляционное отношение применимо для парной и множественной корреляции независимо от формы связи.


