
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Проверочные расчёты передачиСодержание книги
Поиск на нашем сайте
Окружная скорость колёс и степень точности передачи:
При такой скорости следует принять 8-ю степень точности передачи. Коэффициент нагрузки:
Значения КНb даны в [6,табл.3.5]: при y bd =1,1, и симметричном расположении косозубых или шевронных колёс относительно опор с учётом изгиба ведомого вала от натяжения цепной передачи КНb =1,13. По [6,табл.3.4, с.32] при V=5,01м/с и 8-й степени точности КНa =1,09. По [6,табл.3.6, c.32] для шевронных колёс при V=5,01м/с КНn =1,01.
Проверка контактных напряжений производится по формуле:
[s]H – допускаемое расчетное контактное напряжение, [s]H=675МПа; КН – коэффициент нагрузки, КН =1,4; Т 2 – вращающий момент на валу колеса, Т 2 =152,2Н·м; y ва – коэффициент ширины зубчатого венца, y ва=0,4; u – передаточное число, u =5;
Оценка степени использования материала:
Недогрузка в 6,06% допустима. Проверяем зубья на выносливость по напряжениям изгиба по формуле:
Допускаемое расчетное контактное напряжение [s]F=286МПа; Коэффициент нагрузки:
По таблице [6, т.3.7] при
Коэффициент прочности зуба по местным напряжениям YF, зависящий от эквивалентного числа зубьев zv: у шестерни: у колеса: При этом YF 1=4,28; YF 2 =3,62. Находим отношения для шестерни: для колеса: Далее рассчитываем зубья колеса, для которого найденное отношение меньше. Определяем коэффициенты Yb и
для средних значений коэффициента торцового перекрытия ea =1,5 и 8-й степени точности.
Произведем проверочные расчеты на прочность при пиковой нагрузке:
Tпуск/T = 1,3 (по техническому заданию);
Tпуск/T = 1,3 (по техническому заданию);
Условия прочности при пиковой нагрузке выполнены.
Определение сил, действующих в зацеплении Силы, действующие в зацеплении: - окружная - радиальная В цилиндрической шевронной передаче осевые силы, действующие на каждую половину шеврона, уравновешиваются.
Расчет цепной передачи
Выбираем приводную роликовую трехрядную цепь; Вращающий момент на ведущей звездочке:
Передаточное число было принято ранее:
Определяем числа зубьев звездочек: - ведущей: - ведомой: Тогда фактическое передаточное число передачи:
Отклонение от заданного составляет:
Произведем расчет коэффициента эксплуатации передачи:
Для определения шага цепи задаемся величиной допускаемого давления
Выбираем по таблице цепь: 3ПР-25,4-170,1 по ГОСТ 13568. Параметры цепи: - предельная статическая нагрузка - масса одного метра цепи - площадь проекции опорной поверхности шарнира - шаг цепи Средняя скорость цепи:
Окружная сила:
Давление в шарнирах:
Уточняем по таблице допускаемое давление:
Условие Определяем число звеньев цепи по формуле:
Предварительное межосевое расстояние:
Уточняем межосевое расстояние цепной передачи:
Для свободного провисания цепи предусматривается возможность уменьшения межосевого расстояния на 0,4%, то есть:
Длина цепи:
Определяем диаметры делительных окружностей звездочек:
Определяем диаметры окружностей вершин зубьев звездочек:
Радиус впадин профилей зубьев при диаметре роликов цепи
Определяем диаметры окружностей впадин зубьев звездочек:
Диаметры ободов звездочек при ширине пластины цепи
Ширина зуба трехрядной звездочки при расстоянии между внутренними пластинами
Минимальная ширина венца звездочек при расстоянии между венцами зубьев
Проверяем статическую прочность цепи, для чего рассчитываем силы, действующие на нее. Окружная сила:
Натяжение цепи от действия центробежных сил:
Натяжение, обусловленное силой тяжести ветви цепи:
Нагрузка на валы и опоры:
Натяжение ведущей ветви цепи:
Проверяем запас прочности цепи:
Так как нормативный коэффициент запаса прочности
|
||||||
|
Последнее изменение этой страницы: 2016-12-10; просмотров: 145; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.59.218.229 (0.008 с.) |

 , где
, где - угловая скорость шестерни;
- угловая скорость шестерни; - диаметр шестерни;
- диаметр шестерни; м/с.
м/с. , где
, где .
. , где
, где – ширина шестерни,
– ширина шестерни, 


 , где
, где .
. и симметричном расположении косозубых или шевронных зубчатых колес относительно опор КFb =1,13, КFn =1,4,
и симметричном расположении косозубых или шевронных зубчатых колес относительно опор КFb =1,13, КFn =1,4,  =0,91.
=0,91. .
. ;
;  ;
; ;
;  ;
; :
: МПа;
МПа; МПа;
МПа;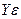 :
: ;
;  ;
;
 ,
,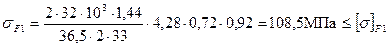
 где
где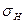 - контактные напряжения,
- контактные напряжения,  - максимальные контактные напряжения;
- максимальные контактные напряжения;

 где
где - напряжения изгиба,
- напряжения изгиба,  - максимальные напряжения изгиба;
- максимальные напряжения изгиба;

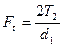
 ;
;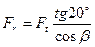 ;
;  ;
; Н·м
Н·м .
. (так как
(так как  );
);

 .
. где
где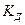 =1 – коэффициент динамичности нагрузки;
=1 – коэффициент динамичности нагрузки; =1 – коэффициент, учитывающий влияние межосевого расстояния;
=1 – коэффициент, учитывающий влияние межосевого расстояния; =1 – коэффициент, учитывающий расположения передачи;
=1 – коэффициент, учитывающий расположения передачи;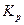 =1 – коэффициент, учитывающий способ регулировки передачи;
=1 – коэффициент, учитывающий способ регулировки передачи; =1 – коэффициент, учитывающий способ смазывания цепи;
=1 – коэффициент, учитывающий способ смазывания цепи; =1,25 – коэффициент режима работы;
=1,25 – коэффициент режима работы; =1 – коэффициент, учитывающий температуру окружающей среды.
=1 – коэффициент, учитывающий температуру окружающей среды. .
. . Ведущая звездочка имеет частоту вращения n=145об/мин. Среднее значение допускаемого давления при n=200об/мин,
. Ведущая звездочка имеет частоту вращения n=145об/мин. Среднее значение допускаемого давления при n=200об/мин,  , где
, где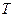 - вращающий момент на ведущей звездочке, Т=578,7Н·м;
- вращающий момент на ведущей звездочке, Т=578,7Н·м; - коэффициент эксплуатации,
- коэффициент эксплуатации,  - число зубьев ведущей звездочки,
- число зубьев ведущей звездочки,  - коэффициент рядности,
- коэффициент рядности, 
 ;
; ;
; ;
; .
. , где
, где - шаг цепи,
- шаг цепи,  - число оборотов ведущей звёздочки,
- число оборотов ведущей звёздочки, 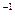 ;
;
 , где
, где - угловая скорость,
- угловая скорость, 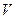 - скорость цепи,
- скорость цепи,  .
.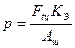 , где
, где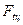 - окружная сила,
- окружная сила,  - площадь опоры шарнира,
- площадь опоры шарнира,  .
. .
.
 МПа.
МПа. выполнено.
выполнено. , где
, где ;
;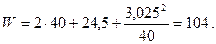
 ;
; мм.
мм.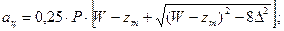
 .
. ;
; мм.
мм.
 мм.
мм. , где
, где мм;
мм; - число зубьев звёздочек.
- число зубьев звёздочек.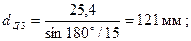


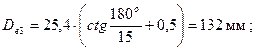


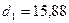 мм:
мм: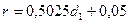 ;
; мм.
мм. ;
; мм;
мм;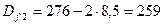 мм.
мм. мм:
мм: ;
;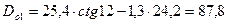 мм;
мм; мм.
мм.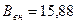 мм:
мм:
 мм.
мм. мм:
мм:
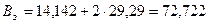 мм.
мм. .
. ;
; .
. ;
;


 где
где - коэффициент динамичности;
- коэффициент динамичности;  .
. Н.
Н.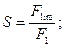
 .
. ; следовательно, условие прочности
; следовательно, условие прочности  выполняется.
выполняется.


