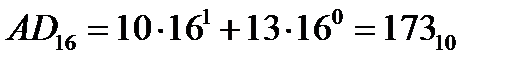Перевод чисел из одной системы счисления в другую – перевод чисел с основаниями, являющимися степенью 2, перевод целых и дробных чисел По правилам, По степенному ряду, По правилу Горнера

Для преобразования восьмеричных и шестнадцатеричных чисел в двоичные, необходимо каждую восьмеричную цифру заменить тремя двоичными, шестнадцатеричную – четырьмя.

Преобразование из восьмеричной в шестнадцатеричную возможно с помощью предварительного перевода в двоичную.

Общая формула.

Если число в системе C необходимо перевести в систему S, то для этого нужно провести его последовательное деление на основание системы S, выраженное в системе C. На каждом шаге деления получают цифры числа в системе S, начиная с младшей. Процесс деления заканчивается, когда частное станет меньше S.

Схема Горнера

.

10101101,10101₂=173,65625₁₀

10101101₂ = ((((((1·2+0)·2+1)·2+0)·2+1)·2+1)·2+0)·2+1 = 173₁₀

0,10101₂ = 0,5(1+0,5(0+0,5(1+0,5(0+1·0,5)))) = 0,65625₁₀

 

154,25₈=108,32812

154₈=(1*8+5)*8+4=108₁₀

0,25₈=1/8*(2+5*1/8)=0,32812₁₀

 

2FA,14₁₆=762,07812

2FA₁₆=(2*16+15)*16+10=762₁₀

0,14₁₆=1/16*(1+4*1/16)=0,07812₁₀

 

Правило перевода целых чисел:

1) последовательно делить переводимое число, а затем получаемые целые частные на основание новой системы счисления, выраженное цифрами исходной системы до тех пор, пока частное не станет равным нулю или меньшим делителя.

2) Полученные остатки, являющиеся цифрами числа в новой системе счисления, привести в соответствие с алфавитом новой системы счисления.

3) Составить число в новой системе счисления, записывая его, начиная с последнего остатка

Правило перевода дробных чисел:

1) Последовательно умножать переводимое число, а затем получаемые дробные части произведений на основание новой системы, выраженное цифрами исходной системы до тех пор, пока дробная часть не будет равной нулю или не будет достигнута заданная точность

2) Полученные целые части произведений, являющиеся цифрами числа в новой системе счисления, привести в соответствие с алфавитом новой системы счисления.

3) Составить дробную часть числа в новой системе счисления, начиная с целой части первого произведения.

Пример:

 

 

 

173₁₀=10101101₂=255₈=AD₁₆

 

 

 

 

0,65625₁₀=0,10101₂=0,52₈=0,A8₁₆

 

 

Способ записи числа в виде степенного ряда можно использовать для чисел в любой системе счисления и применять его для перевода чисел в десятичную систему счисления.

Для того чтобы перевести двоичное, восьмеричное, шестнадцатеричное число в десятичную систему счисления способом степенного ряда следует:

1. Обозначить координаты степенной оси, учитывая, что ноль ставится под младшим целым разрядом исходного числа, а возрастание координат степенной оси идет справа налево.

2. Записать сумму произведений каждой цифры числа на основание системы счисления исходного числа в степени, соответствующей координате степенной оси.

3. Подсчитать сумму произведений степенного ряда.