
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Алгоритм нахождения обратной матрицы.Содержание книги
Поиск на нашем сайте
1)Сначала проверим является ли А квадратной, т.е. совпадают ли n и k. 2)Затем проверим равен ли определитель мартицы А нулю. Если он равен нулю, то обратной матрицы не существует. 3)С помощью матрицы алгебраических дополнений
Полученная матрица A −1 и будет обратной. Иначе говоря, обратная матрица равна единице, делённой на определитель исходной матрицы и умноженной на транспонированную матрицу алгебраических дополнений элементов исходной матрицы. Определение системы m уравнений с n неизвестными. Система m линейных алгебраических уравнений с n неизвестными в линейной алгебре — это система уравнений вида
Здесь
Исследование решений системы линейных уравнений. 1) Δ ≠0 система имеет единственное решение 2) Δ=0, а хотя бы один из вспомогательных ≠0, то решений нет 3) Δ= Δ1= Δ2= Δ3=0 бесчисленное множество решений Определение основной матрицы системы. Если имеем систему линейных уравнений, то таблица, составленная из коэффициентов при неизвестных, называется основной матрицей системы. Определение расширенной матрицы системы. Если к основной матрице добавить столбец свободных членов, то получим расширенную матрицу системы. Определение однородной системы линейных уравнений. Однородной системой m линейных уравнений с n неизвестными называется система вида
19.!Исследование решений системы линейных однородных уравнений. 20. Δ ≠0 система имеет единственное решение 21. Δ=0, а хотя бы один из вспомогательных ≠0, то решений нет 22. Δ= Δ1= Δ2= Δ3=0 бесчисленное множество решений Матричная форма записи системы линейных уравнений.
Запись решения системы линейных уравнений в матричном виде. Первоначально надо проверить, имеет ли система уравнений решение по теореме Кронекера-Копелли. Затем для решения матричным методом необходимо ввести в рассмотрение матрицы-столбцы для неизвестных X и свободных членов B. Тогда систему линейных уравнений можно записать в матричной форме AX=B. Умножив это матричное уравнение на A-1, получим A-1AX= A-1B, откуда EX=X=A-1B. Следовательно, матрица-решение X легко находится как произведение A-1 и B. Определение ранга матрицы. Рангом матрицы А называется наивысший порядок отличного от нуля минора матрицы.
|
||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-10; просмотров: 356; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.96 (0.008 с.) |


 — транспонированная матрица алгебраических дополнений;
— транспонированная матрица алгебраических дополнений;
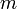 — количество уравнений, а
— количество уравнений, а 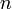 — количество неизвестных.
— количество неизвестных. , где
, где 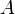 — основная матрица системы,
— основная матрица системы,  и
и  — столбцы свободных членов и решений системы соответственно:
— столбцы свободных членов и решений системы соответственно:



