Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Фазочастотная характеристика схемыСодержание книги Поиск на нашем сайте
В силу наличия трёх конденсаторов (С1, С2, С3) по сравнению со средними частотами на низких частотах существует фазовый сдвиг выходного сигнала по отношению к входному (максимальный сдвиг 3π/2). Значения ЛФЧХ в области низких частот: Для области низких частот:
график ЛФЧХ в области низких частот приведен на рисунке 2.8 Данные для построения ЛФЧХ приведены в таблице 2.6 Таблица 2.6 – данные для построения ЛФЧХ в области низких частот
Рисунок 2.8 график ЛФЧХ в области низких частот
Для области высоких частот:
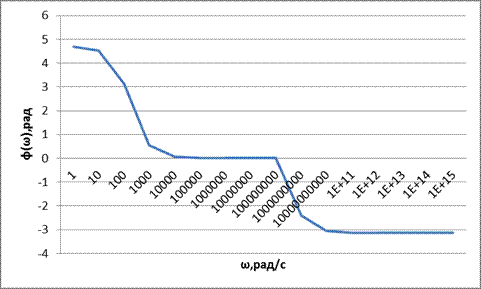
график ЛФЧХ в области высоких частот приведен на рисунке 2.9 Данные для построения ЛФЧХ приведены в таблице 2.7 Таблица 2.7 – данные для построения ЛФЧХ в области высоких частот
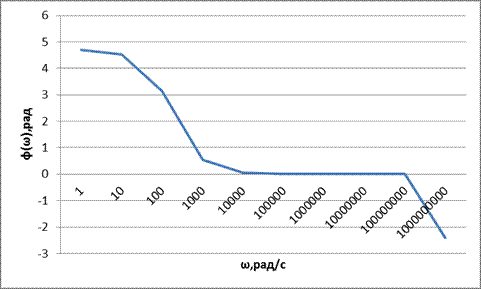
Рисунок 2.10 график ЛФЧХ в области высоких частот Итоговая фазочастотная характеристика изображена на рисунке 2.11 Данные для построения ФЧХ приведены в таблице 2.8 Таблица 2.8 – данные для построения ЛФЧХ
Рисунок 2.11 – график ЛФЧХ
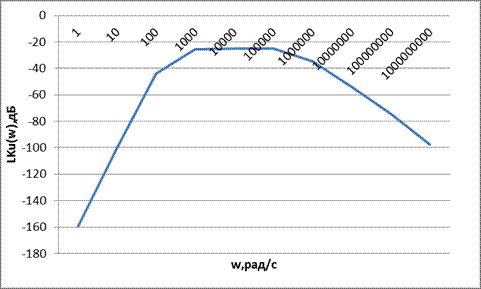
Рисунок 2.12 — итоговые графики ЛАЧХ и ЛФЧХ Определяем рабочий диапазон частот (диапазон, на котором коэффициент передачи по напряжению уменьшается в Рабочий диапазон частот схемы: 850Гц – 0,3МГц. Поступление на вход схемы последовательности прямоугольных импульсов Для построения временной диаграммы работы схемы при поступлении на ее вход последовательности положительных прямоугольных импульсов с длительностью импульса tИ = 10 мс и скважностью предварительно определяется переходная характеристика схемы h(t) отдельно для малых времен (соответствует передаче фронта прямоугольного импульса) и для больших времен (соответствует передаче крыши прямоугольного импульса). Построенная на данном этапе временная диаграмма позволяет оценить искажения, внесенные схемой при передаче заданной последовательности импульсов: определить спад крыши импульса и длительность фронта. Расчет производим отдельно для малых времен (соответствует передаче фронта прямоугольного импульса) и для больших времен (соответствует передаче крыши прямоугольного импульса).
Нахождение переходной характеристики схемы h(t) Для малых времён. Будем производить расчёт для малых времён (что соответствует передаче фронта прямоугольного импульса) и для больших времён (соответствует передаче крыши импульса).
Так как знаменатель полученного выражения имеет один корень равный 0, а остальные отличные от 0, то для нахождения оригинала удобно применить вторую формулу Хевисайда:
где
где pk - корни знаменателя, при которых B(p) становится равным нулю, n - число корней знаменателя. А(pk) - значение числителя H(p) при p=pk B'(pk) - значение первой производной знаменателя по переменной p при p=pk Ищем корни многочлена Имеем:
Производная:
После подстановки и соответствующих преобразований выражение для переходной функци h(t) примет вид:
График зависимости h(t) в области малых времён представлен на рисунке 2.13 Данные для построения зависимости h(t) в области малых времён приведен в таблице 2.9 Таблица 2.9- Данные для построения зависимости h(t) в области малых времён
рисунке 2.13 - график зависимости h(t) для малых времён
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-13; просмотров: 348; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.219.127.59 (0.007 с.) |

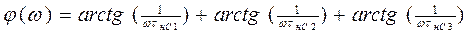 (2.47)
(2.47)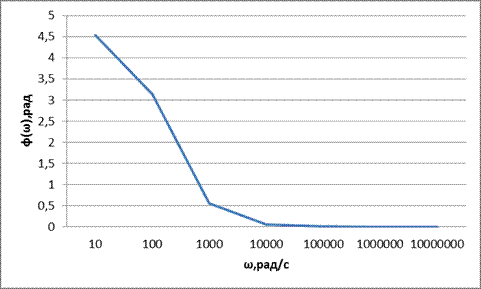
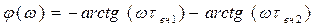 (2.48)
(2.48)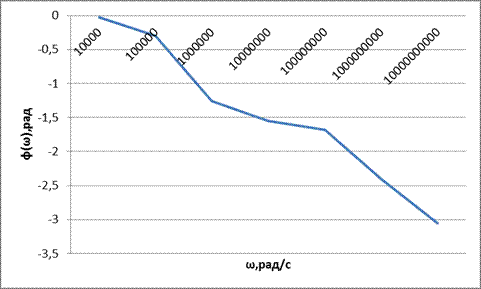
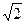 раз).
раз).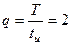 , имеющих амплитуду Um=10 мВ,
, имеющих амплитуду Um=10 мВ,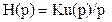 (2.49) Расчёт для области малых времён:
(2.49) Расчёт для области малых времён: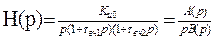 (2.50)
(2.50)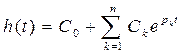 (2.51)
(2.51) , а
, а 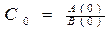
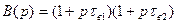
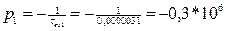 ,
, 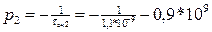 (2.52)
(2.52)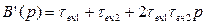 (2.53)
(2.53)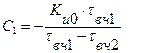
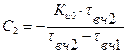 (2.54)
(2.54)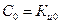
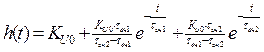 (2.55)
(2.55)