
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Поправки вычисленные и эмпирическиеСодержание книги
Поиск на нашем сайте
Во многих экспериментах для учета систематических эффектов необходимо вводить поправки. При этом всегда следует отдавать предпочтение эмпирическим методам, т.е. методам, основанным на измерениях, а не теоретическим вычислениям. Последние могут оказаться ошибочными по целому ряду причин - неверна теория, неправильные предположения, ошибки вычисления, - тогда как эмпирические методы по самой своей сущности в меньшей степени подвержены ошибкам. Допустим, например, что мы исследуем вопрос о том, в какой мере некоторая жидкость пропускает свет с данной длиной волны. Мы наливаем жидкость в стеклянную кювету, стенки которой перпендикулярны направлению светового пучка, и в точках X и Y измеряем интенсивность света оказался не зависящим от
Рис. 34.5. Установка для измерения коэффициента поглощения света в жидкости.
Чтобы найти поправку теоретическим путем, следовало бы измерить толщину стенок и по таблицам физических констант найти ослабление, вызываемое данной толщиной стекла данного сорта при данной длине световой волны. Даже если подобная информация получена, поправка будет зависеть от того, насколько точно нам известна толщина стенок - а они, скорее всего, неоднородны, - и поэтому требуется аккуратно усреднить эту величину по поперечному сечению светового пучка. Такая поправка будет зависеть также от того, насколько точно мы знаем длину волны света, и, помимо всего, от того, в какой мере табличные данные соответствуют сорту стекла, из которого сделана наша кювета. Эмпирический же метод состоит в том, что сначала мы измеряем интенсивности в точках X и Y с пустой кюветой, а затем, не меняя ее положение относительно светового пучка, кювету заполняем жидкостью и повторяем измерения. Вы видите, что при таком методе отпадают все перечисленные выше трудности. Хотя эмпирические поправки следует предпочитать теоретическим, лучше всего определять поправки обоими методами и проверять, насколько они согласуются. Это будет еще одним достоинством вашего эксперимента.
Относительные методы
Ранее мы говорили о том, как при помощи потенциометра измеряют отношение сопротивлений двух резисторов. Это типичный пример относительного метода. Величина Рассмотрим еще один пример - измерение вязкости жидкости методом, основанным на формуле Пуазейля для течения жидкости по капилляру. Эта формула имеет вид:
где Теперь посмотрим на прибор, изображенный на рисунке 34.6. Это вискозиметр Оствальда. В баллон А заливают определенный объем жидкости с плотностью
Рис. 34.6. Вискозиметр Оствальда
Величины, которые стоят в правой части уравнения, сравнительно просто измерить. Заметим, что при таком относительном методе полностью устраняются две трудные операции, необходимые при абсолютном методе. Первая - поддержание постоянного перепада давления и его измерение, вторая - измерение внутреннего радиуса капилляра, которое следует проводить с особой тщательностью, ибо в формулу входит величина Относительными методами измеряются и такие величины, как мощность источника радиоактивного излучения, яркость источника света, плотность потока излучения радиогалактики, ускорение силы тяжести. Во всех этих случаях проводить абсолютные измерения весьма трудно и поэтому обычно измеряют относительные величины. Отметим и то, что определив абсолютное значение измеряемой величины для одного образца или объекта, мы превращаем тем самым все относительные значения в абсолютные.
Предварительный эксперимент
В реальных экспериментах в противоположность учебным лабораторным работам почти всегда сначала ставят пробные опыты, которые преследуют сразу несколько целей. а) Экспериментатор "знакомится" с данным экспериментом. В каждом эксперименте своя методика и связанные с нею определенные, часто повторяющиеся операции, и экспериментатору необходимо поупражняться или попрактиковаться в их выполнении. Первые несколько измерений в эксперименте почти всегда менее надежны или менее ценны, чем последующие, и обычно удается сэкономить время если в начальный период работы затратить часть его на то, чтобы найти наилучший способ проведения измерений и записи результатов. б) Проверяется работа отдельных элементов установки и аппаратуры. в) Определяется соответствующий интервал значений для каждой из величин, изменяющихся в данном эксперименте. г) Оцениваются возможные ошибки в различных величинах. Как мы уже видели, это оказывает непосредственное влияние на стратегию самого эксперимента в том смысле, что больше внимания уделяют измерению тех величин, ошибка которых вносит основной вклад в ошибку конечного результата. Пункты в) и г) можно рассматривать как выражение той мысли, что всякий серьёзный эксперимент следует заранее планировать, а при планировании несколько пробных измерений гораздо полезней, чем сто теорий. Конечно, план должен быть достаточно гибким, и его обычно подправляют в ходе самого эксперимента. Но даже самый примитивный план всегда лучше, нежели проводить одно измерение за другим в зависимости от того, что вдруг придет вам в голову. Всегда, кроме случаев простейших экспериментов, следует проводить некоторые предварительные измерения и составить план с указанием величин, которые необходимо измерить, и времени, отводимого на каждое такое измерение. То же самое относится и к каждому узлу аппаратуры. Прежде, чем приступить к систематическим измерениям, убедитесь, что вы знаете, как он работает. Если имеется руководство с описанием аппаратуры или инструкции производителя, прежде всего, прочитайте их. Это выглядит совершенно очевидным. И, тем не менее, очень многие не могут взять в толк простых вещей, когда дело доходит до экспериментальной работы. Сложные методы обработки результатов измерений и устранение незаметных на глаз ошибок - все это прекрасно, но не может заменить вам простого здравого смысла.
Проверка очевидного
Если считается, что установка механически устойчива, проверьте, не качается ли она. Не забывайте, что плоскость определяется тремя точками, не лежащими на одной прямой. Поэтому лучше всего, если у прибора три ножки и их концы образуют равносторонний треугольник. Когда ножек больше трех, прибор, поставленный на плоскую поверхность, шатается, если концы ножек не лежат в одной плоскости. Если считается, что основание прибора установлено горизонтально, все же взгляните и проверьте хотя бы приблизительно, так ли это. Если потом потребуется выверить установку точнее, то можно всегда воспользоваться спиртовым уровнем. При проведении оптических экспериментов убедитесь, что все отражающие и преломляющие поверхности выглядят достаточно чистыми, для недорогостоящей оптики известен прекрасный способ — подышать на поверхность и быстро ее протереть. Но никогда не протирайте тряпкой или носовым платком дорогостоящие линзы! Они изготавливаются из мягкого стекла и к тому же часто покрыты очень тонким слоем — толщиной около 100 нм — минеральных солей для уменьшения отражающей способности. Такие линзы легко поцарапать. Их никогда не следует касаться пальцами и хранить открытыми. Чаще всего с них достаточно просто смахнуть пыль мягкой кисточкой из верблюжьего волоса или, в крайнем случае, осторожно протереть специально предназначенной тканью. Убедитесь в том, что оптические детали, которые должны быть соосными, действительно соосны и линзы расположены примерно под прямым углом к направлению светового пучка. Просто удивительно, как часто приходится наблюдать такую картину: студент мучается с оптической системой, не замечая, что важнейшая ее линза покрыта пленкой жира, стоит на несколько миллиметров выше или ниже, чем нужно, или повернута примерно на 10° относительно нормали. Если вам трудно поймать изображение, которое требуется, например, при методе Бойса, поймайте сначала изображение своего пальца. Точно так же, не найдя в спектрометре изображения при помощи зрительной трубы, уберите ее и попробуйте обнаружить изображение на глаз. После этого снова поставьте трубу. В опытах по электричеству, когда вам приходится иметь дело с клеммными соединениями проводов, проверьте, хорошо ли последние зачищены,— если необходимо, зачистите их — и убедитесь, что клеммы плотно затянуты. Если требуется спаять два провода, то, прежде всего, зачистите их концы, а затем покрепче соедините их механически. Посмотрите, полностью ли пропаяно все соединение. Когда место пайки остынет, слегка подергайте за каждый из проводов, чтобы убедиться в том, что припой пристал к металлу и что у вас не получился просто механический контакт. Если вы пользуетесь гальванометром или другим аналогичным прибором с переключателем чувствительности, то сначала всегда ставьте переключатель в положение, соответствующее наименьшей чувствительности. Когда вы собираете электросхему, которая питается от сети, всегда включайте ее в сеть в самую последнюю очередь, и если вам надо в ней что-то изменить, не полагайтесь на выключенный тумблер сети, а выньте штепсель из сетевой розетки.
Субъективные ошибки
Проводя измерения, вы должны рассматривать себя как некий элемент аппаратуры, который также может вносить погрешность. Постарайтесь выяснить, какие ошибки свойственны лично вам. Есть люди, которые, оценивая десятые доли деления по шкале прибора, склонны избегать тех или иных цифр. Вы можете легко себя проверить, хотя это не так уж и важно. Но что уже более серьезно, так это ошибки, которые можно назвать субъективными. Никто из нас не застрахован от случайных ошибок при списывании показаний прибора или при арифметических подсчетах. Но допустим, что некоторая серия измерений дает результат, который вам кажется завышенным. Вполне может оказаться, что в этом случае вы будете делать ошибок больше обычного, и, вероятнее всего, таких, которые ведут к снижению результата. Конечно, если вы не знаете заранее, чего ожидать, то вы гарантированы от подобной опасности. Часто бывает так, что ее невозможно избежать, но иногда достаточно просто изменить процедуру измерения. Допустим, например, что вы измеряете при помощи секундомера время, за которое совершается сто колебаний маятника. Вы записываете: Начальный отсчет 0’0.2”. Конечный отсчет 1’49.7”. Время ста колебаний 1’49.5”. Но второй отсчет сделан неверно: должно быть 1’39.7”. Вы сбрасываете показания секундомера и повторяете измерение. Стрелка останавливается примерно в том же положении. Вы ожидаете, что она покажет приблизительно 1’49”, и вполне возможно, что вы повторите свою ошибку. И, конечно, ничто не говорит вам об этом — оба результата прекрасно согласуются. Но допустим, что вы не останавливаете секундомер. После второй сотни колебаний часы показывают 3’19.1”, и это показание вы записываете точно. На вторую серию колебаний затрачено 1’29.4”, т. е. налицо допущенная где-то ошибка, которая сразу бросается в глаза. Заметим, что даже если вы повторите ошибку и запишете 3'29.1'', то после вычитания предыдущего результата обнаружите какое-то расхождение. Вообще говоря, человек делает меньше ошибок в том случае, когда он чувствует себя комфортабельно — и в прямом, и в переносном смысле слова. Поэтому стоит потратить немного времени на то, чтобы создать соответствующие условия, особенно при длительных измерениях. а) Аппаратура, требующая регулировки, и ручки управления, которыми часто приходится пользоваться, должны быть удобно расположены. б) То же самое относится и к приборам, с которых часто приходится снимать показания. Вообще говори, показания снимать удобнее с вертикальной шкалы, нежели с горизонтальной, а еще лучше, если шкала немного наклонена назад. в) Необходимо хорошее общее освещение. (В оптических экспериментах, конечно, нужно стараться устранить рассеянный свет.) г) Необходимо обеспечить хорошую вентиляцию. Крайне важно, чтобы в лаборатории был свежий и не слишком теплый воздух. д) И, наконец, следует подыскать удобное место для ведения записи, желательно подальше от источников воды и тепла.
Повторные измерения
Измерение отдельной величины необходимо повторить, по крайней мере, еще один раз. Такое повторение: А) помогает избежать ошибки при снятии показаний приборов и их записи, Б) дает возможность оценить ошибку измерений. Но если вы проводите серию измерений пары величин, по которым хотите определить наклон наилучшей прямой линии, то нет никакой необходимости измерять несколько раз y при каждом значении x. Как только вы провели такие измерения дважды, т.е. нашли две точки на прямой, вы тут же получили некоторое значение наклона. Вам нужен еще ряд значений y, но для этого лучше проводить далее измерения при других значениях x, чем повторять при одних и тех же. Иногда приходится измерять величины x и y, связанные нелинейной зависимостью y (x). Пусть, к примеру, y - амплитуда колебаний простой гармонической системы, на которую действует внешняя периодическая сила с частотой x. На рисунке 34.7 представлен типичный набор экспериментальных значений x и y вблизи резонанса. В данном случае для более точного определения наилучшей линии нужно, чтобы точки были как можно ближе друг к другу. Но и здесь нет необходимости повторять одни и те же измерения. Мерой ошибки служит разброс точек относительно наилучшей линии, хотя, конечно, для проверки неплохо повторить несколько раз измерения величины y при одном или двух значениях x. В вопросе повторения измерений есть одна сторона, которую можно пояснить на одном не столь уж редком примере. При проведении измерений студент получил два значения измеряемой величины 56.30 и 60.12. Точность измерений он оценил примерно в 0.5 и пришел к выводу, что один из результатов неверен.
Рис. 34.7. Амплитуда колебаний простой гармонической системы как функция частоты внешней силы
Спрашивать, какой из результатов неверен, смешно. Ведь цель эксперимента - что-либо найти. Студент нашел, что один из его результатов неверен. В подобной ситуации вы обязаны провести дополнительные измерения. Измерения следует проводить до тех пор, пока результаты не приобретут какой-то смысл. А до этого с ними нельзя проводить никаких, даже простейших действий. Если следующее измерение дает 56.34, то можно будет подумать, что неверен, вероятно, второй результат. Нужно еще раз измерить угол призмы, и если он окажется равным 56.35, то вы можете быть почти уверены, что так оно и есть. Вы можете даже задуматься над тем, как это вы сумели получить угол, равный 60.12. Но этого, пожалуй, уже никогда не удастся установить. По-видимому, во время измерений была случайно сдвинута призма, или, что более вероятно, была сбита установка зрительной трубы, или просто неверно произведен отсчет. досадно, когда появляется неверный результат и вы не можете его объяснить, но так бывает, и если это случается редко, то не следует расстраиваться. Беспокоиться придется в том случае, если а) вы произвольно решите, что угол призмы равен 60, и поэтому примете второй результат или б) решите усреднить первые два результата.
Обработка результатов
Если эксперимент длится достаточно долго, то всегда следует стараться обрабатывать результаты в ходе эксперимента. Очень плохо, когда проводят все новые и новые измерения, а их результаты обрабатываются лишь в конце эксперимента. Во-первых, вычисления значительно лучше проводить, пока все свежо в вашей памяти. Во-вторых, при обработке части результатов нередко обнаруживается какое-либо расхождение, которое приводит к необходимости внести те или иные изменения в аппаратуре. Если же это обнаруживается лишь через продолжительное время после измерений, то вы расстроитесь значительно сильнее. Кроме того, и сама работа ведется часто так, что одной серией результатов определяется дальнейшее направление эксперимента. И уж самое глупое, что можно сделать, - это разобрать установку до того, как обработать результаты.
Систематические погрешности
|
||||
|
Последнее изменение этой страницы: 2016-12-13; просмотров: 137; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.239.145 (0.012 с.) |

 и
и  (рис. 34.5). Пусть для простоты коэффициент пропускания
(рис. 34.5). Пусть для простоты коэффициент пропускания 
 , соответствующую толще жидкости
, соответствующую толще жидкости  . Кювета не может быть абсолютно прозрачной, и поэтому в результаты измерений необходимо ввести поправку на ослабление света двумя стенками.
. Кювета не может быть абсолютно прозрачной, и поэтому в результаты измерений необходимо ввести поправку на ослабление света двумя стенками.
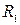 измеряется не абсолютно, а в единицах (или относительно) величины
измеряется не абсолютно, а в единицах (или относительно) величины 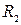 . Относительные измерения имеют очень важное значение в физике. Их можно провести точнее и они проще, нежели абсолютные, и очень часто они дают все, что нужно.
. Относительные измерения имеют очень важное значение в физике. Их можно провести точнее и они проще, нежели абсолютные, и очень часто они дают все, что нужно. ,
,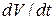 - расход жидкости,
- расход жидкости, 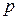 - перепад давления вдоль трубки длиной
- перепад давления вдоль трубки длиной  ,
,  - внутренний радиус капилляра,
- внутренний радиус капилляра, 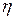 - коэффициент вязкости жидкости. Установив постоянный перепад давления вдоль трубки и измерив его, а также величины
- коэффициент вязкости жидкости. Установив постоянный перепад давления вдоль трубки и измерив его, а также величины 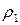 и коэффициентом вязкости
и коэффициентом вязкости  , а затем эту жидкость засасывают в баллон В, причем верхний ее уровень устанавливают чуть выше отметки
, а затем эту жидкость засасывают в баллон В, причем верхний ее уровень устанавливают чуть выше отметки  . После этого измеряют время
. После этого измеряют время 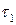 , за которое уровень жидкости опускается от
, за которое уровень жидкости опускается от  . Затем данная жидкость заменяется другой, плотность которой
. Затем данная жидкость заменяется другой, плотность которой  и коэффициент вязкости
и коэффициент вязкости  . Для этой жидкости также измеряем соответствующее время
. Для этой жидкости также измеряем соответствующее время  . Легко показать, что отношение вязкостей дается формулой
. Легко показать, что отношение вязкостей дается формулой





