
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Которым должна удовлетворять реляционная база данных.Содержание книги
Поиск на нашем сайте
1. Правило информации. Информация в реляционной базе данных должна быть представлена исключительно на логическом уровне и только в таблицах, все значения в таблице должны быть атомарными. 2. Правило гарантированного доступа. Доступ к таблице должен осуществляться только с использованием имени таблицы, именем атрибута, ключа. 3. Поддержка недействительных значений. Настоящая реляционная база данных должна позволять вводить неопределенное значение (null) и должны быть значения которые есть, но пока нам не известны. 4. Правило динамического каталога, основанного на реляционной модели. Доступ к описанию базы данных осуществляется по тем же правилам, что и к реально хранимым данным. 5. Правило исчерпывающего подъязыка данных. Языки могут быть разные, они должны содержать: · Описание данных; · Описание представлений – части информации, нужной для конкретного представления; · Обработка данных – интерактивная и программная. Интерактивная – запрос и тут же ответ, а программная – пишем программу запросов, обрабатываем, получаем результат. · Условия целостности. Целостность должна поддерживаться на уровне доменов, на уровне атрибутов, на уровне соответствия атрибутов. Кроме ссылочной целостности еще есть объектная целостность (в объектной таблице должны быть уникальные кортежи). Каскадное удаление означает, что при удалении объекта, удаляются и все его связи. · Идентификация прав доступа пользователя к данным. Это необходимо для исключения несанкционированного доступа. · Границы транзакции (начало – завершение - отмена). Транзакция – это работа, которая должна быть либо целиком выполнена, либо целиком не выполнена. 6. правило обновления представлений. 7. Правило добавления, обновления и удаления. Таблицы должны позволять добавлять, удалять и корректировать записи. 8. Правило физической независимости данных. 9. Правило логической независимости данных. 10. Правило независимости условий целостности. Условия целостности должны храниться в базе данных, а не в программе. 11. Правило независимости условий распространения. Реляционная база данных не должна быть привязана к конкретным потребностям конкретного пользователя. 12. Правило единственности.
Работа с базой данных должна осуществляться на едином языке. И никакой язык низкого уровня не должен позволять обходить ограничения. Операции над данными. Существует три класса операций: 1. Реляционная алгебра – процедурный язык, операндами выступают таблицы, и в ответе мы тоже получаем таблицы. 2. Исчисление кортежей (SQL) – декларативный язык. В качестве переменных выступают кортежи. 3. Исчисление доменов (QBE). В качестве переменных выступают столбцы. Реляционная алгебра. Договоримся, что малыми латинскими буквами мы будем обозначать таблицы, большими латинскими буквами – атрибуты и множества атрибутов. Например, r(R) – это таблица r со множеством атрибутов R. R(A,B,C.D) – ключевые атрибуты подчеркиваются - R={A,B,C,D}. Операции: 1. Операция объединения. Эта операция определена над двумя таблицами с одинаковой схемой, в результате получается третья таблица с такой же схемой, которая сдержит кортежи из первой и второй таблицы без повторений. Пример: r(A,B,C) a1bc1 a2bc a1bc1 abc1 a1bc1 abc1 ab1c ab1c ab1c a2bc 2. Операция разность. Эта операция определена над двумя таблицами с одинаковой схемой, результатом является третья таблица с такой же схемой, в которой есть кортежи, которые есть в первой таблице, но нет во второй. Пример: r(A,B,C) \ s(A,B,C) = q(A,B,C) a1bc1 a2bc abc1 abc1 a1bc1 ab1c ab1c 3. Декартово произведение. Операция определена над двумя таблицами с произвольной схемой, в результате получаем третью таблицу, в схеме которой используются все атрибуты обоих таблиц, каждый кортеж образуется комбинацией кортежей первой таблицы с каждым кортежем второй таблицы. r(A,B) ab cd abcd a1b cd1 abcd1 a1bcd a1bcd1 4. Операция пересечения. Эта операция не является основной, ее можно выразить через операцию разности: r Эта операция определена над двумя таблицами с одинаковыми схемами, в результате получается третья таблица с той же самой схемой, которая содержит данные, встречающиеся в первой и второй таблице. Пример: r(A,B) ab ab ab a1b1 a1b a1b a1b a2b2 a2b1 5. Операция селекции ( Операция определена над одной таблицей, в результате получаем таблицу с той же схемой, в которой те кортежи, которые удовлетворяют записанному условию. Пример: R(A,B,C) 123 123 245 138
При этом дублирование не допускается.
6. Операция проекции ( В качестве исходных данных имеем одну таблицу и в ответе одну таблицу, которая содержит только указанные столбцы. X Пример: R(A,B,C) 112 1 11 11 не фиксируется 123 2 21 12 145 41 14 223 22 22 7. Операция соединения (основная).
Существует внутренняя операция соединения и внешняя, при этом внешняя делится на правую и левую. · Внутренняя а) естественное соединение – осуществляется по равенству значений в одноименных столбцах. Одноименные столбцы имеют одно и тоже имя и определены на одних и тех же доменах. Для соединения используются две таблицы, в результате получаем третью таблицу, кортежи которой получаются комбинацией тех кортежей из исходных таблиц, которые имеют одинаковые значения в одноименных столбцах. Операция соединения коммутативна относительно операндов, т.е. от перестановки мест результат не изменяется.
112 11a 112a 113 11b 112b 123 42c 113a 145 113b 421 421c операция соединения для таблиц с одинаковыми схемами равносильна операции пересечения:
11 11 11 12 42 42 Операция соединения для таблиц с разными схемами равносильна декартовому произведению:
11 cd 11cd 12 c1d 11c1d 14 12cd 42 12c1d 14cd 14c1d 42cd 42c1d б) Тета-соединение ( Это соединение не обязательно по равенству, операция соединения происходит по любой операции сравнения( Тета-соединение осуществляется не обязательно по одноименным столбцам, а по разным тоже, но столбцы должны быть определены на одних и тех же доменах.
B=D a1c 1e a1c1e a12c 1e1 a1c1e1 a11c2 2e a2c2e a13c 2e1 a12c2e1 a11c21e a11c21e1
B>D a1c 1e a12c1e a12c 1e1 a12c1e1 a11c2 2e a13c1e1 a13c 2e1 a13c1e a13c2e a13c2e · внешнее соединение. Рассмотрим на примере естественного соединения. тогда внешнее соединение выполняется по тем же правилам, что и естественное, но в ответ выписываются строки из левой таблицы, если соединение левое (из правой таблицы, если соединение правое). Пример:
left 1ac 1d 1acd 2a1c 2d 1acd1 1ac1 1d1 2a1cd 3ac 1ac1d 4a1c 1ac1d1 3ac null 4a1c null 8. операция деления. (операция обратная декартовому произведению). Пусть нам дано: r(R), s(S), тогда а r’( То есть нужно найти такое отношение r’, что оно будучи декартово перемножено с s дает приблизительно r. Пример: r(A,B,C,D) s(C,D) r[CD abef ef ab abcd dc ef abdf efdc efef afdc Проверка: r’ abef efef abdc efdc операция деления равносильна квантору общности в математической логике. Эту операцию можно выразить через другие операции:
Убедимся, что операция деления равносильна квантору общности: Пусть у нас есть данные о том, какой пилот каким типом самолета может управлять – Право (пилот, тип самолета) Иванов ТУ 154 Иванов ИЛ 62 Иванов ЯК 42 Петров ТУ 154 Петров ИЛ 62 Смирнов ТУ 154 Смирнов ИЛ 62 Смирнов ЯК 42 Смирнов АН 24 Панин ИЛ 62 Запрос: найти пилотов, которые могут управлять всеми типами самолетов из следующего списка: ТУ 154; Ил 62; ЯК 42; То есть q(тип самолета) ТУ 154 Ил 62 ЯК 42 право Иванов Смирнов Запрос: нужно найти пилотов, которые умеют управлять самолетом ТУ 154 q’(тип самолета) ТУ 154 Право Иванов Петров Смирнов
|
||||||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 191; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.76.111 (0.007 с.) |

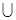 s(A,B,C) = q(A,B,C)
s(A,B,C) = q(A,B,C) s(C,D) = q(A,B,C,D)
s(C,D) = q(A,B,C,D)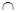 s=r\(r\s).
s=r\(r\s).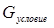 ).
).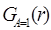 = g(A,B,C)
= g(A,B,C)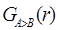 = q’(A,B,C)
= q’(A,B,C)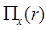 ).
). R – X является подмножеством R.
R – X является подмножеством R. =q(A)
=q(A) 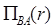 = q’(B,A)=q’(A,B) порядок столбцов
= q’(B,A)=q’(A,B) порядок столбцов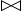 Обозначение: Join или
Обозначение: Join или  .
. 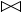 r(A,B,C) s(A,B,D) = q(A,B,C,D)
r(A,B,C) s(A,B,D) = q(A,B,C,D)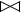 r(A,B) s(A,B) = q(A,B)
r(A,B) s(A,B) = q(A,B)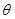 ).
).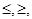 =(эквивалентное соединение),<>, <,>).
=(эквивалентное соединение),<>, <,>).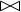 r(A,B,C) s(D,E) = q (A,B,C,D,E)
r(A,B,C) s(D,E) = q (A,B,C,D,E)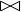 r(A,B,C) s(A,D) = q(A,B,C,D)
r(A,B,C) s(A,D) = q(A,B,C,D)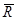 =R\S,
=R\S,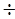 s={t|
s={t| 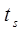
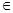 S
S 
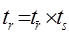 }, где r’- частное.
}, где r’- частное. CD]s = r’(A,B)
CD]s = r’(A,B)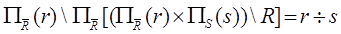
 q’
q’


