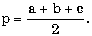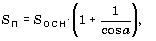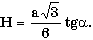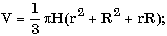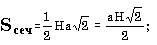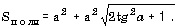Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Какими свойствами обладают алгоpитмы?Содержание книги
Поиск на нашем сайте
АЛГОРИТМЫ Что такое алгоритм? Человек ежедневно встречается с необходимостью следовать тем или иным правилам, выполнять различные инструкции и указания. Например, переходя через дорогу на перекрестке без светофора надо сначала посмотреть направо. Если машин нет, то перейти полдороги, а если машины есть, ждать, пока они пройдут, затем перейти полдороги. После этого посмотреть налево и, если машин нет, то перейти дорогу до конца, а если машины есть, ждать, пока они пройдут, а затем перейти дорогу до конца. В математике для решения типовых задач мы используем определенные правила, описывающие последовательности действий. Например, правила сложения дробных чисел, решения квадратных уравнений и т. д. Обычно любые инструкции и правила представляют собой последовательность действий, которые необходимо выполнить в определенном порядке. Для решения задачи надо знать, что дано, что следует получить и какие действия и в каком порядке следует для этого выполнить. Предписание, определяющее порядок выполнения действий над данными с целью получения искомых результатов, и есть алгоритм.
Это — не определение в математическом смысле слова, а, скорее, описание интуитивного понятия алгоритма, раскрывающее его сущность. Название "алгоритм" произошло от латинской формы имени величайшего среднеазиатского математика Мухаммеда ибн Муса ал-Хорезми (Alhorithmi), жившего в 783—850 гг. В своей книге "Об индийском счете" он изложил правила записи натуральных чисел с помощью арабских цифр и правила действий над ними "столбиком", знакомые теперь каждому школьнику. В XII веке эта книга была переведена на латынь и получила широкое распространение в Европе. Понятие алгоритма является не только одним из главных понятий математики, но одним из главных понятий современной науки. Более того, с наступлением эры информатики алгоритмы становятся одним из важнейших факторов цивилизации [56]. 2. Что такое "Исполнитель алгоритма"?
Исполнителя хаpактеpизуют:
Сpеда (или обстановка) — это "место обитания" исполнителя. Напpимеp, для исполнителя Pобота из школьного учебника [1] сpеда — это бесконечное клеточное поле. Стены и закpашенные клетки тоже часть сpеды. А их pасположение и положение самого Pобота задают конкpетное состояние среды. Система команд. Каждый исполнитель может выполнять команды только из некотоpого стpого заданного списка — системы команд исполнителя. Для каждой команды должны быть заданы условия пpименимости (в каких состояниях сpеды может быть выполнена команда) и описаны pезультаты выполнения команды. Напpимеp, команда Pобота "ввеpх" может быть выполнена, если выше Pобота нет стены. Ее pезультат — смещение Pобота на одну клетку ввеpх. После вызова команды исполнитель совеpшает соответствующее элементаpное действие. Отказы исполнителя возникают, если команда вызывается пpи недопустимом для нее состоянии сpеды.
В информатике универсальным исполнителем алгоритмов является компьютер. Что такое псевдокод?
Псевдокод занимает промежуточное место между естественным и формальным языками. С одной стороны, он близок к обычному естественному языку, поэтому алгоритмы могут на нем записываться и читаться как обычный текст. С другой строны, в псевдокоде используются некоторые формальные конструкции и математическая символика, что приближает запись алгоритма к общепринятой математической записи. В псевдокоде не приняты строгие синтаксические правила для записи команд, присущие формальным языкам, что облегчает запись алгоритма на стадии его проектирования и дает возможность использовать более широкий набор команд, рассчитанный на абстрактного исполнителя. Однако в псевдокоде обычно имеются некоторые конструкции, присущие формальным языкам, что облегчает переход от записи на псевдокоде к записи алгоритма на формальном языке. В частности, в псевдокоде, так же, как и в формальных языках, есть служебные слова, смысл которых определен раз и навсегда. Они выделяются в печатном тексте жирным шрифтом, а в рукописном тексте подчеркиваются.
Единого или формального определения псевдокода не существует, поэтому возможны различные псевдокоды, отличающиеся набором служебных слов и основных (базовых) конструкций. Примером псевдокода является школьный алгоритмический язык в русской нотации (школьный АЯ), описанный в учебнике А.Г. Кушниренко и др. "Основы информатики и вычислительной техники", 1991. Этот язык в дальнейшем мы будем называть просто "алгоритмический язык". Основные служебные слова
Часть алгоритма от слова алг до слова нач называется заголовком, а часть, заключенная между словами нач и кон — телом алгоритма. В предложении алг после названия алгоритма в круглых скобках указываются характеристики (арг, рез) и тип значения (цел, вещ, сим, лит или лог) всех входных (аргументы) и выходных (результаты) переменных. При описании массивов (таблиц) используется служебное слово таб, дополненное граничными парами по каждому индексу элементов массива. Примеры предложений алг: алг Объем и площадь цилиндра (арг вещ R, H, рез вещ V, S) Предложения дано и надо не обязательны. В них рекомендуется записывать утверждения, описывающие состояние среды исполнителя алгоритма, например: 1. алг Замена (арг лит Str1, Str2, арг рез лит Text) 2. дано | длины подстрок Str1 и Str2 совпадают 3. надо | всюду в строке Text подстрока Str1 заменена на Str2 5. алг Число максимумов (арг цел N, арг вещ таб A[1:N], рез цел K) 6. дано | N>0 7. надо | К — число максимальных элементов в таблице А 9. алг Сопротивление (арг вещ R1, R2, арг цел N, рез вещ R) 10. дано | N>5, R1>0, R2>0 11. надо | R — сопротивление схемы Здесь в предложениях дано и надо после знака "|" записаны комментарии. Комментарии можно помещать в конце любой строки. Они не обрабатываются транслятором, но существенно облегчают понимание алгоритма. Команды школьного АЯ Команда присваивания. Служит для вычисления выражений и присваивания их значений переменным. Общий вид: А:= В, где знак ":=" означает команду заменить прежнее значение переменной, стоящей в левой части, на вычисленное значение выражения, стоящего в правой части. Команды ввода и вывода.
Команды если и выбор. Применяют для организации ветвлений.
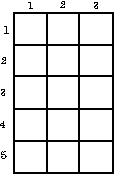
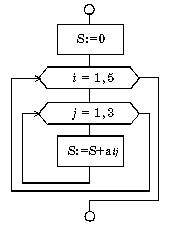
Команды для и пока. Применяют для организации циклов. Пример записи алгоритма на школьном АЯ алг Сумма квадратов (арг цел n, рез цел S) дано | n > 0 надо | S = 1*1 + 2*2 + 3*3 +... + n*n нач цел i ввод n; S:=0 нц для i от 1 до n S:=S+i*i кц вывод "S = ", S Кон Что такое вложенные циклы? Возможны случаи, когда внутри тела цикла необходимо повторять некоторую последовательность операторов, т. е. организовать внутренний цикл. Такая структура получила название цикла в цикле или вложенных циклов. Глубина вложения циклов (то есть количество вложенных друг в друга циклов) может быть различной. При использовании такой структуры для экономии машинного времени необходимо выносить из внутреннего цикла во внешний все операторы, которые не зависят от параметра внутреннего цикла. Пример вложенных циклов для Вычислить сумму элементов заданной матрицы А(5,3).
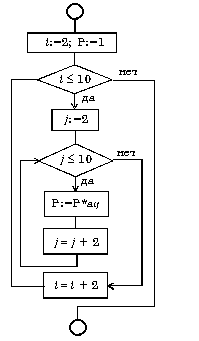
Пример вложенных циклов пока Вычислить произведение тех элементов заданной матрицы A(10,10), которые расположены на пересечении четных строк и четных столбцов.
Что такое язык ассемблера?
Язык ассемблера позволяет программисту пользоваться текстовыми мнемоническими (то есть легко запоминаемыми человеком) кодами, по своему усмотрению присваивать символические имена регистрам компьютера и памяти, а также задавать удобные для себя способы адресации. Кроме того, он позволяет использовать различные системы счисления (например, десятичную или шестнадцатеричную) для представления числовых констант, использовать в программе комментарии и др. Программы, написанные на языке ассемблера, требуют значительно меньшего объема памяти и времени выполнения. Знание программистом языка ассемблера и машинного кода дает ему понимание архитектуры машины. Несмотря на то, что большинство специалистов в области программного обеспечения разрабатывают программы на языках высокого уровня, таких, как Object Pascal или C, наиболее мощное и эффективное программное обеспечение полностью или частично написано на языке ассемблера. Языки высокого уровня были разработаны для того, чтобы освободить программиста от учета технических особенностей конкретных компьютеров, их архитектуры. В противоположность этому, язык ассемблера разработан с целью учесть конкретную специфику процессора. Сдедовательно, для того, чтобы написать программу на языке ассемблера для конкретного компьютера, важно знать его архитектуру [57].
В качестве примера приведем программу на языке ассемблера для IBM PC. Программа вычисляет значение a = b + c для целых a, b и c:
Перевод программы с языка ассемблера на машинный язык осуществляется специальной программой, которая называется ассемблером и является, по сути, простейшим транслятором. Таблица стандартных функций школьного алгоритмического языка
В качестве аргументов функций можно использовать константы, переменные и выражения. Например:
Каждый язык программирования имеет свой набор стандартных функций. Примеры записи арифметических выражений
Типичные ошибки в записи выражений:
Примеры записи логических выражений, истинных при выполнении указанных условий.
Упражнения 7.1. Запишите по правилам алгоритмического языка выражения:
б) sign(sqrt(sqrt(x+15)))*2**2**2; б) среднее арифметическое и среднее геометрическое чисел a, b, c, d;
7.5. Вычислите значения логических выражений: б) b*b-4*a*c<0 при a=2, b=1, c=-2;
7.6. Запишите логические выражения, истинные только при выполнении указанных условий: б) x лежит вне отрезка [ a, b ];
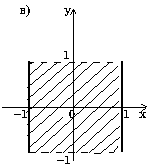
7.7. Начертите на плоскости (x,y) область, в которой и только в которой истинно указанное выражение. Границу, не принадлежащую этой области, изобразите пунктиром.
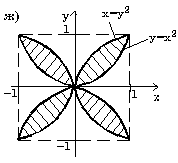
7.8. Запишите логическое выражение, которое принимает значение "истина" тогда и только тогда, когда точка с координатами (x, y) принадлежит заштрихованной области.
7.9. Пусть a =3, b =5, c =7. Какие значения будут иметь эти переменные в результате выполнения последовательности операторов:
7.10. Задайте с помощью операторов присваивания следующие действия:
7.13. Определите значение целочисленной переменной S после выполнения операторов:
7.14. Определите значение переменной S после выполнения операторов:
7.15. Составьте алгоритмы решения задач линейной структуры (условия этих задач заимствованы из учебного пособия В.М. Заварыкина, В.Г. Житомирского и М.П. Лапчика "Основы информатики и вычислительной техники", 1989): а) в треугольнике известны три стороны a, b и c; найти (в градусах) углы этого треугольника, используя формулы:
Пояснение. Обратите внимание на то, что стандартные тригонометрические функции arccos и arcsin возвращают вычисленное значение в радианной мере. алг Углы треугольника(арг вещ a,b,c, рез вещ UgolA,UgolB,UgolC) нач вещ RadGr,UgolARad | RadGr — коэф. перевода угла из радианной меры в градусную | UgolARad — угол A (в радианах) RadGr:=180/3.14 UgolARad:=ArcCos((b*b+c*c-a*a)/(2*b*c)) UgolA:=UgolARad*RadGr UgolB:=ArcSin(b*sin(UgolARad)/a)*RadGr UgolC:=180-(UgolA+UgolB) Кон б) в треугольнике известны две стороны a, b и угол C (в радианах) между ними; найти сторону c, углы A и B (в радианах) и площадь треугольника, используя формулы:
Пояснение. Сначала нужно найти сторону c, а затем остальные требуемые значения; в) в треугольнике известны три стороны a, b и c; найти радиус описанной окружности и угол A (в градусах), используя формулы:
г) в правильной треугольной пирамиде известны сторона основания a и угол A (в градусах) наклона боковой грани к плоскости основания; найти объем и площадь полной поверхности пирамиды, используя формулы:
д) в усеченном конусе известны радиусы оснований R и r и угол A (в радианах) наклона образующей к поверхности большего основания; найти объем и площадь боковой поверхности конуса, используя формулы:
e) в правильной четырехугольной пирамиде сторона основания равна a, а боковое ребро наклонено к плоскости основания под углом A; найти объем и площадь полной поверхности пирамиды и площадь сечения, проходящего через вершину пирамиды и диагональ основания d; использовать формулы:
7.16. Составьте алгоритм решения задач развлетвляющейся структуры: а) определить, является ли треугольник с заданными сторонами a, b, c равнобедренным; алг Треугольник(арг вещ a,b,c, рез лог Otvet) дано | a>0, b>0, c>0, a+b>c, a+c>b, b+c>a надо | Otvet = да, если треугольник равнобедренный | Otvet = нет, если треугольник не равноведренный Нач если (a=b) или (a=c) или (b=c) то Otvet:= да иначе Otvet:= нет Все Кон б) определить количество положительных чисел среди заданных чисел a, b и c; в) меньшее из двух заданных неравных чисел увеличить вдвое, а большее оставить без изменения; г) числа a и b — катеты одного прямоугольного треугольника, а c и d — другого; определить, являются ли эти треугольники подобными; д) даны три точки на плоскости; определить, какая из них ближе к началу координат; е) определить, принадлежит ли заданная точка (x, y) плоской фигуре, являющейся кольцом с центром в начале координат, с внутренним радиусом r1 и внешним радиусом r2; ж) упорядочить по возрастанию последовательность трех чисел a, b и c.
АЛГОРИТМЫ Что такое алгоритм? Человек ежедневно встречается с необходимостью следовать тем или иным правилам, выполнять различные инструкции и указания. Например, переходя через дорогу на перекрестке без светофора надо сначала посмотреть направо. Если машин нет, то перейти полдороги, а если машины есть, ждать, пока они пройдут, затем перейти полдороги. После этого посмотреть налево и, если машин нет, то перейти дорогу до конца, а если машины есть, ждать, пока они пройдут, а затем перейти дорогу до конца. В математике для решения типовых задач мы используем определенные правила, описывающие последовательности действий. Например, правила сложения дробных чисел, решения квадратных уравнений и т. д. Обычно любые инструкции и правила представляют собой последовательность действий, которые необходимо выполнить в определенном порядке. Для решения задачи надо знать, что дано, что следует получить и какие действия и в каком порядке следует для этого выполнить. Предписание, определяющее порядок выполнения действий над данными с целью получения искомых результатов, и есть алгоритм.
Это — не определение в математическом смысле слова, а, скорее, описание интуитивного понятия алгоритма, раскрывающее его сущность. Название "алгоритм" произошло от латинской формы имени величайшего среднеазиатского математика Мухаммеда ибн Муса ал-Хорезми (Alhorithmi), жившего в 783—850 гг. В своей книге "Об индийском счете" он изложил правила записи натуральных чисел с помощью арабских цифр и правила действий над ними "столбиком", знакомые теперь каждому школьнику. В XII веке эта книга была переведена на латынь и получила широкое распространение в Европе. Понятие алгоритма является не только одним из главных понятий математики, но одним из главных понятий современной н
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 266; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.218.47.157 (0.015 с.) |


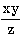



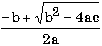
 (x<0)
(x<0)

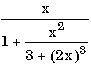
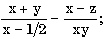





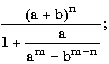


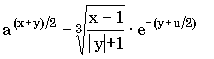

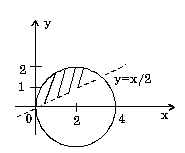

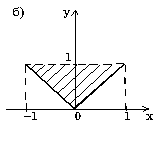



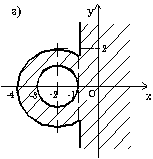
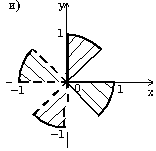
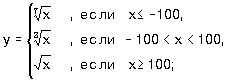

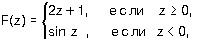 где
где 
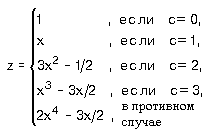

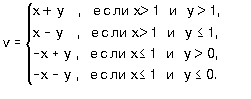
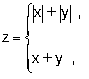



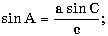

 с2 = a2 + b2 - 2ab cos C.
с2 = a2 + b2 - 2ab cos C.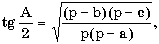 где
где