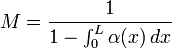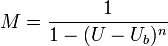часть iii. Внешний фотоэффект и его применение в фотодиодах

 

В 1887 г. немецкий физик Генрих Герц экспериментировал с разрядником для излучения электромагнитных волн - парой металлических шаров. Он заметил, что проскакивание искры между электродами разрядника облегчается, если отрицательно заряженный электрод осветить ультрафиолетовыми лучами. Таким образом, был обнаружен внешний фотоэффект.

В 1888 г. Вильгельм Гальвакс установил, что облучённая ультрафиолетовым светом металлическая пластинка заряжается положительно. Так произошло второе открытие фотоэффекта. Третьим, не зная об опытах Герца и Гальвакса, его наблюдал в том же году итальянец Аугусто Риги. Он выяснил, что фотоэффект возможен и в металлах, и в диэлектриках. Александр Григорьевич Столетов был четвёртым учёным, независимо от других открывшим фотоэффект. Он два года исследовал новое явление и вывел его основные закономерности. Оказалось, что сила фототока, во-первых, прямо пропорциональна интенсивности падающего света, а во-вторых, при фиксированной интенсивности облучения сначала растёт по мере повышения разности потенциалов, но, достигнув определённого значения (ток насыщения), уже не увеличивается.

В 1898 г. немец Филипп Ленард и англичанин Джозеф Томсон доказали, что падающий на металлическую поверхность свет выбивает из неё электроны, движение которых и приводит к появлению фототока. Однако понять природу фотоэффекта с помощью классической электродинамики так и не удалось. Необъяснимым оставалось, почему фототок возникал лишь тогда, когда частота падающего света превышала строго определённую для каждого металла величину.

Только в 1905 г. Эйнштейн превратил эту загадку в совершенно прозрачную картину. Он предположил, что электромагнитное излучение не просто испускается порциями - оно и распространяется в пространстве, и поглощается веществом тоже в виде порций - световых квантов (фотонов). Поэтому для возникновения фотоэффекта важна отнюдь не интенсивность падающего светового пучка. Главное, хватает ли отдельному световому кванту энергии, чтобы выбить электрон из вещества. Минимальную энергию, необходимую для этого, называют работой выхода А. В итоге Эйнштейн вывел уравнение фотоэффекта.

Ясно, что фотоэффект может вызывать только световая волна достаточно высокой частоты, а сила фототока пропорциональна интенсивности поглощённого света, то есть числу фотонов, способных выбить электроны из вещества. В 1907 г. Эйнштейн сделал ещё одно уточнение квантовой гипотезы. Почему тело излучает свет только порциями? А потому, отвечал Эйнштейн, что атомы имеют лишь дискретный набор значений энергии. Таким образом, теория излучения и поглощения приняла законченный вид.

В 1922 г. американец Артур Комптон обнаружил, что длина волны рентгеновского излучения изменяется при рассеянии на электронах вещества. Но, по классической электродинамике, длина световой волны при рассеянии меняться не может! Тогда Комптон выполнил расчёт, предположив, что на электронах рассеиваются не волны, а частицы (фотоны). Результат совпал с экспериментальным. Это стало прямым доказательством реальности существования фотонов.

Определение фотоэффекта

Фотоэлектрическим эффектом (фотоэффектом)называют группу явлений, возникающих при взаимодействии света с веществом и заключающихся либо в эмиссии электронов (внешний фотоэффект),либо в изменении электропроводимости вещества или возникновении электродвижущей силы (внутренний фотоэффект).

В фотоэффекте проявляются корпускулярные свойства света. В 1888 Гальвакс показал, что при облучении ультрафиолетовым светом электрически нейтральной металлической пластинки, последняя приобретает положительный заряд. В этом же году Столетов создал первый фотоэлемент и применил его на практике, потом он установил прямую пропорциональность силы фототока интенсивности падающего света. В 1899 Дж. Дж. Томсон и Ф. Ленард доказали, что при фотоэффекте свет выбивает из вещества электроны.

Внешний фотоэффект

Внешний фотоэффект наблюдается в газах на отдельных атомах и молекулах (фотоионизация) и в конденсированных средах.

Внешний фотоэффект в металле можно представить состоящим из трех процессов: поглощение фотона электроном проводимости, в результате чего увеличивается кинетическая энергия электрона; движение электрона к поверхности тела; выход электрона из металла. Этот процесс энергетически описывают уравнением Эйнштейна. Если, освещая металл монохроматическим светом, уменьшать частоту излучения (увеличивать длину волны), то, начиная с некоторого ее значения, называемого красной границей;фотоэффект прекратится.

Экспериментальные исследования показали, что термин «красная граница» не означает, что граница фотоэффекта обязательно попадает в область красного цвета.

Изучение фотоэффекта

 

 

Рис 1

Первые фундаментальные исследования фотоэффекта выполнены русским ученым А.Г. Столетовым. Принципиальная схема для исследования фотоэффекта приведена на рис. 1. Два электрода (катод К из исследуемого металла и анод А – в схеме Столетова применялась металлическая сетка) в вакуумной трубке подключены к батарее так, что с помощью потенциометра R можно изменять не только значение, но и знак подаваемого на них напряжения. Ток, возникающий при освещении катода монохроматическим светом (через кварцевое окошко), измеряется включенным в цепь миллиамперметром. Облучая катод светом различных длин волн, Столетов установил следующие закономерности, не утратившие своего значения до нашего времени: 1) наиболее эффективное действие оказывает ультрафиолетовое излучение; 2) под действием света вещество теряет только отрицательные заряды; 3) сила тока, возникающего под действием света, прямо пропорциональна его интенсивности.

Дж. Дж. Томсон в 1898г. измерил удельный заряд испускаемых под действием света частиц (по отклонению в электрическом и магнитном полях). Эти измерения показали, что под действием света вырываются электроны. На рис. 1 приведена экспериментальная установка для исследования вольт-амперной характеристики фотоэффекта – зависимости фототока 1, образуемого потоком электронов, испускаемых катодом под действием света, от напряжения U между электродами. Такая зависимость соответствующая двум различным освещенностям E_e катода (частота света в обоих случаях одинакова), приведена на рис. 2. По мере увеличения U фототок постепенно возрастает, т.е. все большее число фотоэлектронов достигает анода. Пологий характер кривых показывает, что электроны вылетают из катода с различными скоростями. Максимально значение тока I_нас – фототок насыщения – определяется таким значением U, при котором все электроны, испускаемые катодом, достигают анода:

 

 

I_нас = en,

 

где n – число электронов, испускаемых катодом в 1с.

Из вольт-амперной характеристики следует, что при U = 0 фототок не исчезает. Следовательно, электроны, выбитые светом из катода, обладают некоторой начальной скоростью υ, а значит, и отличной от нуля кинетической энергией и могут достигнуть анода без внешнего поля. Для того чтобы фототок стал равным нулю, необходимо приложить задерживающее напряжение U₀. При U = U₀ ни один из электронов, даже обладающий при вылете из катода максимальной скоростью υ_max, не может преодолеть задерживающего поля и достигнуть анода. Следовательно,

 

 

т.е., измерив задерживающее напряжение U₀, можно определить максимальные значения скорости и кинетической энергии фотоэлектронов.

 

 

При изучении вольт-амперных характеристик разнообразных материалов (важна чистота поверхности, поэтому измерения проводятся в вакууме и на свежих поверхностях) при различных частотах падающего на катод излучения и различных энергетических освещенностях катода и обобщения полученных данных были установлены следующие три закона внешнего фотоэффекта.

1. Закон Столетова: при фиксированной частоте падающего света число фотоэлектронов, вырываемых из катода в единицу времени, пропорционально интенсивности света (сила фототока насыщения пропорциональна энергетической освещенности Е_е катода).

2. Максимальная начальная скорость (максимальная начальная кинетическая энергия) фотоэлектронов не зависит от интенсивности падающего света, а определяется только его частотой ν, а именно линейно возрастает с увеличением частоты.

3. Для каждого вещества существует «красная граница» фотоэффекта, т.е. минимальная частота ν₀ света (зависящая от химической природы вещества и состояния его поверхности), при которой свет любой интенсивности фотоэффекта не вызывает.

Качественное объяснение фотоэффекта с волновой точки зрения на первый взгляд не должно было бы представлять трудностей. Действительно, под действием поля световой волны в металле возникают вынужденные колебания электронов, амплитуда которых (например, при резонансе) может быть достаточной для того, чтобы электроны покинули металл; тогда и наблюдается фотоэффект. Кинетическая энергия, с которой электрон вырывается из металла, должна была бы зависеть от интенсивности падающего света, так как с увеличением последней электрону передавалась бы большая энергия. Однако этот вывод противоречит 2 закону фотоэффекта. Так как, по волновой теории, энергия, передаваемая электронам, пропорциональна интенсивности света, то свет любой частоты, но достаточно большой интенсивности должен был бы вырывать электроны из металла; иными словами, «красной границы» фотоэффекта не должно быть, что противоречит 3 закону фотоэффекта. Кроме того, волновая теория не смогла объяснить безынерционность фотоэффекта, установленную опытами. Таким образом, фотоэффект необъясним с точки зрения волновой теории света.

Уравнение Эйнштейна для внешнего фотоэффекта

А. Эйнштейн в 1905г. показал, что явление фотоэффекта и его закономерности могут быть объяснены на основе предложенной им квантовой теории фотоэффекта. Согласно Эйнштейну, свет частотой ν не только испускается, как это предполагал Планк, но и распространяется в пространстве и поглощается веществом отдельными порциями (квантами), энергия которых ε₀ = hν. Таким образом, распространение света нужно рассматривать не как непрерывный волновой процесс, а как поток локализованных в пространстве дискретных световых квантов, движущихся со скоростью с распространения света в вакууме. Эти кванты электромагнитного излучения получили название фотонов.

По Эйнштейну, каждый квант поглощается только одним электроном. Поэтому число вырванных фотоэлектронов должно быть пропорционально интенсивности света (1 закон фотоэффекта). Безынерционность фотоэффекта объясняется тем, что передача энергии при столкновении фотона с электроном происходит почти мгновенно.

Энергия падающего фотона расходуется на совершение электроном работы выхода А из металла и на сообщение вылетевшему фотоэлектрону кинетической энергии mυ_max/2. По закону сохранения энергии,

 

(1)

 

Уравнение (1) называется уравнением Эйнштейна для внешнего фотоэффекта.

Уравнение Эйнштейна позволяет объяснить 2 и 3 законы фотоэффекта. Из (1) непосредственно следует, что максимальная кинетическая энергия фотоэлектрона линейно возрастает с увеличением частоты падающего излучения и не зависит от его интенсивности (числа фотонов), так как ни А, ни νот интенсивности света не зависят (2 закон фотоэффекта). Так как с уменьшением частоты света кинетическая энергия фотоэлектронов уменьшается (для данного металла А=const), то при некоторой достаточно малой частоте ν=ν₀кинетическая энергия фотоэлектронов станет равной нулю и фотоэффект прекратится (3 закон фотоэффекта). Согласно изложенному, из (1) получим, что

 

ν₀ = А/h (2)

 

и есть «красная граница» фотоэффекта для данного металла. Она зависит лишь от работы выхода электрона, т.е. от химической природы вещества и состояния его поверхности.

Выражение (1) можно записать в виде

 

eU₀ = h(ν -ν₀).

 

Уравнение Эйнштейна было подтверждено опытами Милликена. В его приборе (1916г.) поверхность исследуемого металла подвергалась очистке в вакууме (фотоэффект и работа выхода сильно зависят от состояния поверхности). Исследовалась зависимость максимальной кинетической энергии фотоэлектронов (изменялось задерживающее напряжение U₀) от частоты ν и определялась постоянная Планка. В 1926г. Советские физики П.И. Лукирский (1894-1954) и С.С. Прилежаев для исследования фотоэффекта применили метод вакуумного сферического конденсатора.Анодом в их установке служили посеребренные стенки стеклянного сферического баллона, а катодом – шарик (R ≈ 1.5 см) из исследуемого металла, помещенный в центр сферы. В остальном схема принципиально не отличается от описанной на рис. 1. Такая форма электродов позволила увеличить наклон вольт-амперных характеристик и тем самым более точно определить задерживающее напряжение U₀ (а следовательно, и h). Значение h, полученное из данных опытов, согласуется со значениями, найденными другими методами (по изучению твердого тела и по коротковолновой границе сплошного рентгеновского спектра). Все это является доказательством правильности уравнения Эйнштейна, а вместе с тем и его квантовой теории фотоэффекта.

Если интенсивность света очень большая, то возможен многофотонный (нелинейный) фотоэффект, при котором электрон, испускаемый металлом, может одновременно получить энергию не от одного, а от N фотонов (N = 2 ÷ 7). Уравнение Эйнштейна для многофотонного фотоэффекта:

 

 

В опытах с фокусируемыми лазерными пучками плотность фотонов очень большая, поэтому электрон может поглотить не один, а несколько фотонов. При этом электрон может приобрести энергию, необходимую для выхода из вещества, даже под действием света с частотой, меньшей «красной границы» - порога однофотонного фотоэффекта. В результате «красная граница» смещается в сторону более длинных волн.

Идея Эйнштейна о распространении света в виде потока отдельных фотонов и квантовом характере взаимодействия электромагнитного излучения с веществом подтверждена в 1922г. Опытами А.Ф. Иоффе и Н.И. Добронравова. В электрическом поле плоского конденсатора уравновешивалась заряженная пылинка из висмута. Нижняя обкладка конденсатора изготовлялась из тончайшей алюминиевой фольги, которая являлась одновременно анодом миниатюрной рентгеновской трубки. Анод бомбардировался ускоренными до 12кВ фотоэлектронами, испускаемыми катодом под действием ультрафиолетового излучения. Освещенность катода подбиралась столь слабой, чтобы из него в 1с вырывалось лишь 1000 фотоэлектронов, а следовательно, и число рентгеновских импульсов было 1000 в 1с. Опыт показал, что в среднем через каждые 30 мин уравновешенная пылинка выходила из равновесия, т.е. рентгеновское излучение освобождало из нее фотоэлектрон, приобретающий энергию согласно уравнению Эйнштейна (1).

Если бы рентгеновское излучение распространялось в виде сферических волн, а не отдельных фотонов, то каждый рентгеновский импульс отдавал бы пылинке очень малую часть своей энергии, которая распределялась бы, в свою очередь, между огромным числом электронов, содержащихся в пылинке. Поэтому при таком механизме трудно вообразить, что один из электронов за такое короткое время, как 30 мин, может накопить энергию, достаточную для преодоления работы выхода из пылинки. Напротив, с точки зрения корпускулярной теории это возможно. Так, если рентгеновское излучение распространяется в виде потока дискретных фотонов, то электрон выбивается из пылинки только тогда, когда в нее попадет фотон. Элементарный расчет для выбранных условий дает, что в среднем в пылинку попадает один фотон из 1,8 * 10⁶. Так как в 1с вылетает 1000 фотонов, то в среднем в пылинку будет попадать один фотон в 30 мин, что согласуется с результатами опыта.

Если свет представляет собой поток фотонов, то каждый фотон, попадая в регистрирующий прибор (глаз, фотоэлемент), должен вызывать то или иное действие независимо от других фотонов. Это же означает, что при регистрации слабых световых потоков должны наблюдаться флуктуации их интенсивности. Эти флуктуации слабых потоков видимого света действительно наблюдались С.И. Вавиловым. Наблюдения проводились визуально. Глаз, адаптированный к темноте, обладает довольно резким порогом зрительного ощущения, т.е. воспринимает свет, интенсивность которого не меньше некоторого порога. Для света с λ = 525 нм порог зрительного ощущения соответствует у разных людей примерно 100 - 400 фотонам, падающим на сетчатку за 1с. С.И. Вавилов наблюдал периодически повторяющиеся вспышки света одинаковой длительности. С уменьшением светового потока некоторые вспышки уже не воспринимались глазом, причем, чем слабее был световой поток, тем больше было пропусков вспышек. Это объясняется флуктуациями интенсивности света, т.е. число фотонов оказалось по случайным причинам меньше порогового значения. Таким образом, опыт Вавилова явился наглядным подтверждением квантовых свойств света.

Использование внешнего фотоэффекта в фотодиодах

Принцип работы

При подаче сильного обратного смещения (близкого к напряжению лавинного пробоя, обычно порядка нескольких сотен вольт для кремниевых приборов), происходит усиление фототока (примерно в 100 раз) за счёт ударной ионизации (лавинного умножения) генерированных светом носителей заряда. Суть процесса в том, что энергия образовавшегося под действием света электрона увеличивается под действием внешнего приложенного поля и может превысить порог ионизации вещества, так что столкновение такого «горячего» электрона с электроном из валентной зоны может привести к возникновению новой электрон-дырочной пары, носители заряда которой также будут ускоряться полем и могут стать причиной образования всё новых и новых носителей заряда.

 

 

 

Зависимость тока (I) и коэффициента умножения (M) от обратного напряжения (U) на ЛФД.

Существует ряд формул для коэффициента лавинного умножения (M), довольно информативной является следующая:

 

 

где L — длина обрасти пространственного заряда, а α — коэффициент умножения для электронов (и дырок). Этот коэффициент сильно зависит от приложенного напряжения, температуры и профиля легирования. Отсюда возникает требование хорошей стабилизации питающего напряжения и температуры, либо учёт температуры задающей напряжение схемой.

Ещё одна эмпирическая формула показывает сильную зависимость коэффициента лавинного умножения (M) от приложенного обратного напряжения:

 

 

где U_b — напряжение пробоя. Показатель степени n принимает значения от 2 до 6, в зависимости от характеристик материала и структуры p — n-перехода.

Исходя из того, что в общем случае с возрастанием обратного напряжения растёт и коэффициент усиления, существует ряд технологий, позволяющих повысить напряжение пробоя до более чем 1500 вольт, и получить таким образом усиление более чем в 1000 раз. Следует иметь в виду, что простое повышение напряженности поля без предприятия дополнительных мер может привести к увеличению шумов.

Если требуются очень высокие коэффициенты усиления (10⁵ — 10⁶), возможна эксплуатация некоторых типов ЛФД при напряжениях выше пробойных. В этом случае требуется подавать на фотодиод ограниченные по току быстро спадающие импульсы. Для этого могут использоваться активные и пассивные стабилизаторы тока. Приборы, действующие таким образом работают в режима Гейгера (Geigermode). Этот режим применяется для создания однофотонных детекторов (при условии, что шумы достаточно малы)

Применение. Типичное применение ЛФД — лазерные дальномеры и волоконные линии связи. Среди новых применений можно назвать позитронно-эмиссионную томографию и физику элементарных частиц. В настоящее время уже появляются коммерческие образцы массивов лавинных светодиодов. Сфера применения и эффективность ЛФД зависят от многих факторов. Наиболее важными являются:

· квантовая эффективность, которая показывает, какая доля падающих фотонов приводит к образованию носителей заряда и возникновению тока

· суммарный ток утечек, который складывается из темнового тока и шумов.

Шумы. Электронные шумы могут быть двух типов: последовательные и параллельные. Первые являются следствием дробовых флуктуаций и в основном пропорциональны ёмкости ЛФД, тогда как параллельные связаны с механическими колебаниями прибора и поверхностными токами утечки. Другим источником шума является фактор избыточного шума (excessnoisefactor),F. В нем описываются статистические шумы, которые присущи стохастическому процессу лавинного умножения M в ЛФД. Обычно он выражается следующим образом:

 

 

 

где к — соотношение коэффициентов ударной ионизации для дырок и электронов. Таким образом, увеличение асимметрии коэффициентов ионизации приводит к уменьшению этих помех. К этому стремятся на практике, так как F(M) вносит основной вклад в ограничение разрешающей способности приборов по энергии.

Ограничения по быстродействию

Ограничения на скорость работы накладывают ёмкости, времена транзита электронов и дырок и время лавинного умножения. Ёмкость увеличивается с ростом площади переходов и уменьшением толщины. Время транзита электронов и дырок возрастает с увеличением толщины, что заставляет идти на компромисс между емкостью и временем. Задержки, связанные с лавинным умножением определяются структурой диодов применяемыми материалам, существует зависимость от к.

Технологии изготовления

 

 

Зонная диаграмма лавинного фотодиода на гетероструктуреInP-InGaAs. Фототок образован дырками.

Для создания данного класса приборов может быть использован широкий круг полупроводников:

· Кремний используется для работы в ближнем ИК-диапазоне, при этом имеет малые шумы, связанные с умножением носителей.

· Германий принимает инфракрасные волны длиной до 1.7 мкм, но приборы на его основе имееют заметные шумы.

· InGaAs обеспечивает приём волн длиной от 1.6 мкм, при этом имея меньшие нежели у германия шумы. Обычно этот материал используется для изготовления лавинных фотодиодов на гетероструктурах, также включающих InP в качестве подложки и второго компонента для создания гетероструктуры. Эта система имеет рабочий диапазон в пределах 0,9 — 0,7 мкм. У InGaAs высокий коэффициент поглощения на длинах волн, используемых в телекоммуникации через волоконно-оптические линии связи, таким образом достаточно даже микронных слоёв InGaAs для полного поглощения излучения. Эти материалы обеспечивают небольшие задержки и малые шумы, что позволяет получить устройства с полосой частот более 100 ГГц для простой InP / InGaAs системы и до 400 ГГц для InGaAs на кремнии. Это делает возможным передачу данных на скоростях, превышающих 10 Гбит/с

· Диоды на основе Нитрида галлия используются для работы в ультрафиолетовом диапазоне волн.

· HgCdTe применяется для изготовления диодов, работающих в инфракрасной части спектра, обычно максимальная длина волны составляет около 14 µm. При этом они требуют охлаждения для сокращения темновых токов. Такая система способна обеспечить очень низкий уровень помех.

 

 

заключение

 

Таким образом, в ходе проведения курсового исследования было установлено, что наиболее широко распространены следующие типы p-n-переходов: точечные, сплавные, диффузионные и эпитаксиальные, рассмотрены особенности технологических процессов изготовления этих переходов. Опираясь на исходные данные, была рассчитана контактная разница потенциалов, которая составила 0,417 (В). В третьей главе курсового проекта был рассмотрен внешний фотоэффект и его использование в фотодиодах, а также лавинный фотодиод и его свойства

БИБЛИОГРАФИЧЕСКИЙ СПИСОК ЛИТЕРАТУРЫ

 

1. Анималу А. Квантовая теория кристаллических твердых тел. –М.: Мир, 1981;

2. Блейкмор Дж. Физика твердого тела. –М.: Мир, 1988;

3. Гранитов Г.И. Физика полупроводников и полупроводниковые приборы. –М.: Сов. радио, 1977;

4. Гусев В.Г., Гусев Ю.М. Электроника: Учебное издание. –М.: Высшая школа, 1991;

5. Давыдов А.С. Квантовая механика. –М.: Физматгиз, 1963;

6. Савельев И.В. Курс общей физики. В 3 т. –М.: Наука, 1979. Т.3;

7. Фистуль В.И, Введение в физику полупроводников. –М.: Высшая школа, 1984;

8. Электроника. Энциклопедический словарь. –М.: Советская энциклопедия, 1991.

 

Приложение

 

Обозначения основных величин, принятые в работе

E_c- энергия соответствующая дну запрещённой зоны

E_F- фермиевская энергия

E_k- энергетическая ступень, образующаяся в p–n-переходе

E_max- максимальная напряжённость электрического поля

E_v- энергия соответствующая потолку валентной зоны

F_i- электрическая энергия

F_ip (F_in)- электростатическая энергия в p (n)-области

j- плотность тока

j_g0- плотность тока термогенерации носителей заряда

j_ngp0 (j_pgp0)- плотность дрейфового тока, текущего через p-n-переход из n-области (p-области) в p-область (n-область)

j_ngup0 (j_pgup0)- плотность диффузионного тока, текущего через p-n-переход из n-области (p-области) в p-область (n-область)

j_z0- плотность тока рекомбинации носителей заряда

l₀- ширина р-n перехода.

l_n0 (l_p0) - ширина n (p) -области p-n-перехода

L_s- дебаевская длина

N- результирующая концентрация примеси

n (p)- концентрация электронов (дырок) в полупроводнике

n₀ (p₀)- равновесная концентрация электронов (дырок) в полупроводнике

N_a (N_d)- концентрация акцепторной (донорной) примеси.

n_i- собственная концентрация носителей заряда

n_n (n_p) - концентрация электронов в n (р) области

n_no (n_po)- равновесная концентрация электронов в n (р) области

N_Э (N_Б) - абсолютная величина результирующей примеси в эмиттере (базе)

P(x)- распределение плотности объёмного заряда

p_p (p_n)- концентрация дырок в р (n) области

p_po (p_no)- равновесная концентрация дырок в р (n) области

p_Э (p_Б)- плотность объёмного заряда

q, e- заряд электрона

T- температура окружающей среды

V_k- энергия контактного поля

ε- напряженность электрического поля

ε- относительная диэлектрическая проницаемость полупроводника

ε₀- диэлектрическая постоянная воздуха

μ_n (μ_p)- подвижность электронов (дырок)

τ_ε- время диэлектрической релаксации

φ- электрический потенциал

φ_k- контактная разность потенциалов

φ_T- температурный потенциал

 

Размещено на Allbest.ru

[1]Антизапирающим называют приконтактный слой, обогащённый свободными носителями заряда.

[2] Отношение изменения концентрации носителей заряда к расстоянию на котором это изменение происходит называется градиентом концентрации: gradn =?n/?x = dn/dx

[3] Диффузионным током называют ток, вызванный тепловым движением электронов.

[4] Ток, созданный зарядами, движущимися в полупроводнике из-за наличия электрического поля и градиента потенциала называется дрейфовым током.

[5] Отсутствие вырождения характеризует существенная концентрация носителей заряда собственной электропроводности.