
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Графическое представление цепиСодержание книги
Поиск на нашем сайте
Цепи Маркова
Пусть имеется система S, которая может находиться в состояниях a1,a2,…,ak, и в процессе работы может переходить только в эти состояния. Пример: выключатель, АТС с двумя телефонами. В определенные моменты времени t1,t2,… система может переходить из одного состояния в другое с определенной вероятностью. Переход обозначим: Система, которая переходит в каждое свое состояние в определенные моменты времени, называется дискретной. Если переходы осуществляются не в определенные моменты, а в определенном промежутке времени, то система называется непрерывной. Определение. Цепью Маркова называется последовательность переходов системы из одного состояния в другое, для которых известны Все вероятности переходов обычно записывают в виде матрицы переходов в цепи за один шаг: a1 a2 … ak
Свойства матрицы: 1. 2. Матрица, обладающая такими свойствами, называется вероятностной матрицей. Переход цепи из одного состояния в другое будем называть шагами перехода.
Задание цепи
Для того чтобы задать цепь, нужно знать: 1. Распределение вероятностей состояний в начальный момент, т.е.
1. Матрицу переходов цепи за один шаг -
Графическое представление цепи
Любую цепь всегда можно представить в виде графа. Пример: пусть Р имеет вид: a1 a2 a3
Зная граф переходов, можно получить матрицу переходов. Графическое представление удобно, когда число состояний небольшое: 3 или 4.
Распределение состояний цепи через n-шагов
Пусть имеется цепь. Важным вопросом в теории цепей является распределение вероятностей состояний цепи через n- шагов. Т.е. требуется определить вероятности состояний нахождения цепи через n- шагов.
Пример. a1 a2 a3
Пусть в начальный момент цепь находится в состоянии a1:
Если число состояний цепи большое, то нахождение распределения вероятностей через n- шагов графически бывает неудобным или невозможным, поэтому такую задачу обычно решают аналитическим способом.
Аналитическое решение распределения состояний цепи через n-шагов
Пусть имеем цепь По формуле полной вероятности получим:
В случае k=3 (3 состояния) система (1) примет вид:
Систему (1) обычно называют системой уравнений Колмогорова. Систему (1) удобно записать в матричном виде следующим способом:
p(n-1) P Тогда равенство (2) в матричном виде кратко запишется так:
Систему (3), придавая последовательно значения 1,2,3,…,k, можно переписать так:
Тогда система (3) окончательно примет вид:
Система (4) – система уравнений Колмогорова для нахождения распределения цепи через n- шагов. Пример. (продолжение) 1 способ Для нахождения нужного распределения нужно матрицу переходов P возвести в третью степень. В результате получим:
Для того, чтобы найти распределение вероятностей состояний через n- шагов, если она начинает функционировать из какого-то состояния, то из примера видно, что каждая строка матрицы 2 способ
Замечание. Матрицу переходов
Существование предельного распределения
Потоки вероятностей
1. Пусть имеем цепь с состояниями a1,a2,…,ak,, вероятности которых будут p1,p2,…,pk, и матрицу переходов Потоком вероятностей
Непрерывные цепи Маркова
Рассмотренные выше цепи имели дискретное множество состояний, в которые эта цепь переходила в определённые моменты времени
Характеристики цепей. Как и в дискретном случае переходы в другие состояния будут характеризоваться соответствующими вероятностями.
Цепи Маркова
Пусть имеется система S, которая может находиться в состояниях a1,a2,…,ak, и в процессе работы может переходить только в эти состояния. Пример: выключатель, АТС с двумя телефонами. В определенные моменты времени t1,t2,… система может переходить из одного состояния в другое с определенной вероятностью. Переход обозначим: Система, которая переходит в каждое свое состояние в определенные моменты времени, называется дискретной. Если переходы осуществляются не в определенные моменты, а в определенном промежутке времени, то система называется непрерывной. Определение. Цепью Маркова называется последовательность переходов системы из одного состояния в другое, для которых известны Все вероятности переходов обычно записывают в виде матрицы переходов в цепи за один шаг: a1 a2 … ak
Свойства матрицы: 1. 2. Матрица, обладающая такими свойствами, называется вероятностной матрицей. Переход цепи из одного состояния в другое будем называть шагами перехода.
Задание цепи
Для того чтобы задать цепь, нужно знать: 1. Распределение вероятностей состояний в начальный момент, т.е.
1. Матрицу переходов цепи за один шаг -
Графическое представление цепи
Любую цепь всегда можно представить в виде графа. Пример: пусть Р имеет вид: a1 a2 a3
Зная граф переходов, можно получить матрицу переходов. Графическое представление удобно, когда число состояний небольшое: 3 или 4.
|
||||||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 313; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.226.34.148 (0.01 с.) |

 ,
, 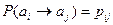 - вероятность соответствующего перехода.
- вероятность соответствующего перехода.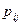 , т.е. вероятности переходов.
, т.е. вероятности переходов.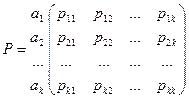

 - сумма элементов любой строки равна 1.
- сумма элементов любой строки равна 1. - начальное распределение (начальный вектор).
- начальное распределение (начальный вектор).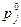 - вероятность того, что цепь находится в состоянии
- вероятность того, что цепь находится в состоянии  ,
,  , т.к. в начальный момент система находится в каком-то состоянии.
, т.к. в начальный момент система находится в каком-то состоянии. .
.
 Каждое состояние будем обозначать точкой (вершина графа), а переходы – дугами.
Каждое состояние будем обозначать точкой (вершина графа), а переходы – дугами.
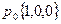 . Требуется определить распределение состояний цепи через 3 шага.
. Требуется определить распределение состояний цепи через 3 шага.





 ,
,  - вероятность того, что через n- шагов цепь (система) будет находиться в состоянии aj, j=1,2,…,k.
- вероятность того, что через n- шагов цепь (система) будет находиться в состоянии aj, j=1,2,…,k. (1)
(1) (1’)
(1’)

 (2)
(2) (3)
(3)

 (4)
(4)

 .
. есть распределение цепи через n- шагов, если она начинается с состояния, номер которого совпадает с номером строки.
есть распределение цепи через n- шагов, если она начинается с состояния, номер которого совпадает с номером строки.

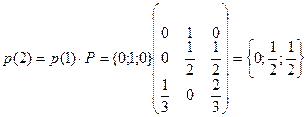

 , аналогично потоком вероятностей
, аналогично потоком вероятностей  называется число
называется число  .
. , такие цепи называются дискретными цепями с дискретным временем. На практике приходится рассматривать цепи с конечным множеством состояний, в которые эта цепь переходит за некоторый промежуток времени
, такие цепи называются дискретными цепями с дискретным временем. На практике приходится рассматривать цепи с конечным множеством состояний, в которые эта цепь переходит за некоторый промежуток времени  .
.  Такие цепи называют дискретными цепями с непрерывным временем или непрерывными цепями.
Такие цепи называют дискретными цепями с непрерывным временем или непрерывными цепями. - вероятность того, что цепь сделает переход
- вероятность того, что цепь сделает переход  за время
за время 


