
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
О случайных событиях с вероятностями близкими к 0 или к 1Содержание книги
Поиск на нашем сайте При решении многих практических задач приходится иметь дело с событиями, вероятность которых очень мала, т.е. близка к нулю. На основании опыта в отношении таких событий принят следующий принцип. Если случайное событие имеет очень малую вероятность, то практически можно считать, что в единичном испытании оно не наступит, иначе говоря, возможностью его появления можно пренебречь. Ответ на вопрос,насколькомалойдолжна быть эта вероятность, определяется существом решаемых задач, тем, насколько важен для нас результат предсказания. Например, если вероятность того, что парашют при прыжке не раскроется равна 0,01, то применение таких парашютов недопустимо. Однако равная той же 0,01 вероятность того, что поезд дальнего следования прибудет с опозданием, делает нас практически уверенными в том, что он прибудет вовремя. Достаточно малую вероятность, при которой (в данной конкретной задаче) событие можно считать практически невозможным, называют уровнем значимости. На практике уровень значимости обычно принимают равным 0,01 (однопроцентный уровень значимости) или 0,05 (пятипроцентный уровень значимости), намного реже он берется равным 0,001. Введение уровня значимости позволяет утверждать, что если некоторое событие А практически невозможно, то противоположное событие Задачи 1. Все натуральные числа от 1 до 30 записаны на одинаковых карточках и помещены в урну. После тщательного перемешивания карточек из урны извлекается одна из них. Какова вероятность того, что число на этой карточке окажется кратным 5? Ответ: 0,2. 2. Какова вероятность того, что в наудачу выбранном двузначном числе цифры одинаковы? Ответ: 0,1. 3. Контролер, проверяя качество 400 изделий, установил, что 20 из них относятся ко второму сорту, а остальные – к первому. Найдите относительную частоту появления изделий 1) первого сорта; 2) второго сорта? Ответ: 1) 0,95; 2)0,05. 4. В цехе работают 7 мужчин и 3 женщины. По табельным номерам наудачу отобраны 2 человека. Найдите вероятность того, что они окажутся мужчинами? Ответ: 7/15. 5. Примерно 1 ребенок из 700 рождается с синдромом Дауна. В больнице большого города в год рождается 3500 детей. Каково ожидаемое число новорожденных с синдромом Дауна? Ответ: 5. 6. Спортсмен стреляет по мишени, разделенной на 3 сектора. Вероятность попадания в первый сектор равна 0,4, во второй – 0,3. Какова вероятность попадания в первый либо во второй сектор? Ответ: 0,7. 7. В большой популяции плодовой мушки у 25% Ответ: 1. 8. Лечение определенного заболевания дает эффект (выздоровление) в 75 % случаев. Оно проводилось шести больным. Какова вероятность того, что: 1) выздоровят все шестеро; 2) не выздоровит ни один? Ответ: 1) 18 %; 2) 0,025 %. 9. Операция пересадки кожи дает успех в 40 % всех случаев. Пациенту делают пересадку кожи несколько раз подряд до тех пор, пока она не удается. Какова вероятность того, что пересадка окажется успешной: 1) с первой попытки; 2) с третьей попытки? Ответ: 1) 0,4 2) 0,144. 10. Студент пришел на экзамен, зная 40 из 50 вопросов программы. В билете 3 вопроса. Найдите вероятность того, что студент ответит на все 3 вопроса билета. Ответ: 0,5. 11. На двух фермах А и В, насчитывающих по 1000 голов крупного рогатого скота, произошла вспышка заболевания ящуром. Доли зараженного скота составляют соответственно 1/5 и 1/4. Какова вероятность того, что выбранная случайным образом корова: 1) принадлежит ферме А и болеет? 2) принадлежит ферме В, болеет и старше одного года, если на каждой ферме 70 % зараженного скота младше одного года? Ответ: 1) 1/10; 2) 3/80. 12. *Одна вакцина формирует иммунитет против краснухи в 95 % случаев. Предположим, что вакцинировалось 30 % популяции и, что вероятность заболеть краснухой у вакцинированного человека без иммунитета такая же, как и у не вакцинированного. Какова вероятность того, что человек, заболевший краснухой, был вакцинирован? Ответ: 3/143. 13. *Некоторое заболевание, которое встречается у 5 % населения, с трудом поддается диагностике. Один грубый тест на это заболевание дает положительные результат (указывающий на наличие заболевания) в 60 % случаев, когда пациент действительно болен, и в 30 % случаев, когда у пациента этого заболевания нет. Пусть для конкретного пациента этот тест дает положительные результат. Какова вероятность того, что у него есть данное заболевание? Ответ: 0,095. 14. *На одном производстве было установлено, что 3 % рабочих являются алкоголиками с показателем прогулов втрое выше, чем у остальных. Если случайно выбранный рабочий отсутствует на работе, то какова вероятность того, что он алкоголик? Ответ: 0,085. 15. *Большая популяция разбита на две группы одинаковой численности. Одна группа придерживалась специальной диеты с высоким содержанием ненасыщенных жиров, а контрольная группа питалась по обычной диете, богатой насыщенными жирами. После 10 лет пребывания на этих диетах возникновение сердечно-сосудистых заболеваний в этих группах составило соответственно 31 % и 48 %. Случайно выбранный из популяции человек страдает сердечно-сосудистым заболеванием. Какова вероятность того, что он принадлежит к контрольной группе? Ответ: 48/79 ≈ 0,61. 16. *Установлено, что курящие мужчины в возрасте свыше 40 лет умирают от рака легких в 10 раз чаще, чем не курящие. В предположении, что 60 % мужской популяции курит, найдите вероятность того, что мужчина, умерший от рака легких, был курящим? Ответ: 15/16 ≈ 0,9375. 17. *Установлено, что в среднем один из 700 детей мужского пола рождается с лишней Y -хромосомой и что среди таких детей крайне агрессивное поведение встречается в 20 раз чаще. Опираясь на эти данные, представьте, что у мальчика крайне агрессивное поведение. Какова вероятность того, что ребенок имеет лишнюю Y -хромосому? Ответ: 20/719 ≈ 0,.28.
|
||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 1547; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.01 с.) |

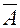 - практически достоверно, т.е. для него Р (
- практически достоверно, т.е. для него Р (


