
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Классическое и статистическоеСодержание книги
Поиск на нашем сайте
МИНИСТЕРСТВО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ
«Утверждаю» Ректор университета __________ А.В. Лагерев «__»___________ 2003 г.
Теория вероятностей И математическая статистика Сборник задач
Брянск 2003
УДК 511 Теория вероятностей и математическая статистика. Сборник задач. – Брянск: БГТУ, 2003. – 59 с.
Разработали: А.И. Горелёнков, канд. техн. наук, доц.; В.М. Кобзев, ст. преп.; А.П. Мысютин, канд. техн. наук, доц.
Рекомендовано кафедрой «Высшая математика» (протокол №3 от 17.03.02).
Научный редактор Н.А. Ольшевская, Э.К. Фёдорова Редактор издательства Л.Н. Мажугина Компьютерный набор А.И. Горелёнков
Темплан 2003 г., п. 9
Предисловие
Настоящий сборник представляет собой систематизированную подборку задач по теории вероятностей и математической статистике. Все задачи снабжены ответами. В начале каждого параграфа приведена сводка основных теоретических положений и формул, необходимых для решения задач. Сборник задач продолжает традицию задачников по теории вероятностей, издававшихся кафедрой высшей математики БГТУ (БИТМ) [4, 5, 9]. Данное издание является переработкой последнего из этих задачников. Добавлено много задач, в частности, составлены параграфы «Комбинаторика», «Неравенство Чебышева», включена новая тема «Элементы математической статистики». Список литературы, приведенный в конце сборника, указывает основные источники, которыми мы пользовались. Большую помощь в подборе задач оказали преподаватели кафедры «Высшая математика» Н.В. Лозинская, Н.А. Ольшевская, Н.Л. Порошина, которым авторы выражают благодарность. Авторы будут признательны всем, заметившим недостатки данного издания и внесшим предложения по его улучшению.
СЛУЧАЙНЫЕ СОБЫТИЯ ЭЛЕМЕНТЫ КОМБИНАТОРИКИ
Правило суммы. Если некоторый объект А может быть выбран из совокупности объектов m способами, а другой объект В может быть выбран n способами, то выбрать либо А, либо В можно m+n способами. Правило произведения. Если объект А можно выбрать из совокупности объектов m способами, и после каждого такого выбора объект В можно выбрать n способами, то пара объектов (А, В) в указанном порядке может быть выбрана mn способами. Размещениемk элементов из n элементов называется упорядоченная выборка (либо расположение в определённом порядке) k из этих элементов. Число размещений из n различных элементов по k элементов без повторений вычисляется по формуле Число размещений из n различных элементов по k элементов с неограниченными повторениями определяется равенством Размещения из n различных элементов по n элементов называются перестановками. Число перестановок из n различных элементов вычисляется по формуле
Число перестановок с повторениями из n элементов, спецификация которых {
Сочетаниемk элементов из n элементов называется выборка k из них без учёта порядка. Число сочетаний из n различных элементов по k элементов без повторений вычисляется по формуле Число сочетаний из n различных элементов по k элементов с неограниченными повторениями определяется равенством
1.1. Сколькими способами можно выбрать три различные краски из имеющихся пяти? 1.2. У одного человека есть 7 книг по математике, а у другого – 9 книг. Сколькими способами они могут обменять одну книгу одного на книгу другого? 1.3. В профком избрано 9 человек. Из них надо выбрать председателя, заместителя, культорга и секретаря. Сколькими способами это можно сделать? 1.4. На диск секретного замка нанесены 10 букв, а секретное слово состоит из 5 букв. Сколько неудачных попыток может быть сделано человеком, не знающим пароля? 1.5. Сколькими способами можно составить трёхцветный полосатый флаг, одна из полос которого должна быть красной, если имеется материал пяти различных цветов? 1.6. Сколькими различными способами можно выполнить групповой портрет пяти человек, если поставить а) их в один ряд; б) трёх человек в первом ряду и двух – во втором? 1.7. Сколькими способами можно расселить девять студентов в трёх комнатах, рассчитанных на трёх человек каждая? 1.8. Сколькими способами можно расставить белые фигуры (2 коня, 1.9. Сколько различных четырёхзначных чисел можно составить из цифр 1.10. В почтовом отделении продаются открытки 10 видов. Сколькими способами можно купить в нём а) 8 открыток; б) 8 различных открыток? 1.11. Номера состоят из двух букв и трёх цифр. Найти число таких номеров, если используются 32 буквы русского алфавита. 1.12. Сколько различных вариантов хоккейной команды можно составить из 1.13. Сколько различных шестизначных чисел можно составить из цифр 1, 2, 3, 4, 5, 6, 7 так, чтобы цифры не повторялись и крайние цифры были чётными? 1.14. Из 10 разных цветков нужно составить букет так, чтобы в него входило не менее 5 цветков. Сколько различных способов существует для составления такого букета, учитывая, что число цветков должно быть нечётным? 1.15. Сколько различных четырёхзначных чисел, делящихся на 4, можно составить из цифр 1, 2, 3, 4, 5?
1.16. В клубе велосипедистов при перерегистрации членских билетов из суеверия перестали использовать цифру 8. Сколько членов было в клубе, если известно, что использованы все трёхзначные номера, не содержащие ни одной 8? 1.17. У одного человека есть 7 книг по математике, а у другого – 9 книг. Сколькими способами они могут обменять 2 книги одного на 2 книги другого? 1.18. Сколько различных четырёхзначных чисел можно составить из цифр 1.19. В колоде 36 карт, из них 4 туза. Сколькими способами можно вынуть 1.20. Сколько различных четырёхзначных чисел можно составить из цифр ОПРЕДЕЛЕНИЕ ВЕРОЯТНОСТИ
Частотой (относительной частотой) события А в данной серии экспериментов называется число Наблюдаемое на практике свойство частоты стабилизироваться возле некоторого числа при неограниченном увеличении объема серии экспериментов называется устойчивостью относительной частоты. При этом число, вокруг которого группируются относительные частоты, называется вероятностьюсобытияА и обозначается P(A) (статистическое определение вероятности). Если пространство элементарных событий W состоит из n равновозможных элементарных событий, то вероятность P(A) события А равна числу m элементарных событий, входящих в А, делённому на число всех элементарных событий n, т.е. Случай равновозможных событий называется классическим, поэтому вероятность 2.1. При испытании партии приборов относительная частота годных приборов оказалась равной 0,9. Найти число годных приборов, если всего было произведено 200 приборов. 2.2. Игральный кубик бросают один раз. Найти вероятности следующих событий: А – появление нечётного числа очков, В – появление не менее пяти очков. 2.3. Монету бросают два раза. Найти вероятность появления хотя бы одного герба. 2.4. Бросают два игральных кубика. Найти вероятности следующих событий: А – сумма очков равна 4, В – сумма очков кратна 3. 2.5. При перевозке 100 деталей, из которых 10 были забракованы, утеряна одна стандартная деталь. Найти вероятность того, что наудачу извлечённая (после перевозки) деталь оказалась стандартной. 2.6. У ребёнка, не умеющего читать, имеются буквы С, И, Г, М, А. Какова вероятность того, что выкладывая их наугад, он получит слово СИГМА? 2.7. Абонент помнит только первые три цифры телефонного номера. Три последние забыл, но знает что они различны. Какова вероятность того, что он наберёт нужный номер? 2.8. К концу дня в магазине осталось 60 арбузов, из которых 50 спелых. Покупатель выбирает 2 арбуза. Какова вероятность того, что выбранные им арбузы будут спелыми? 2.9. У ребёнка, не умеющего читать, имеются буквы А, А, Г, М, М. Какова вероятность того, что выкладывая их наугад, он получит слово ГАММА? 2.10. В партии из 50 изделий 2 бракованных. Для проверки наудачу выбрали 3 изделия. Найти вероятность того, что среди выбранных изделий одно окажется бракованным. 2.11. Абитуриент может на каждом из трёх экзаменов с равными вероятностями получить 2, 3, 4, 5. Какова вероятность его поступления в ВУЗ, если проходной бал – 14? 2.12. В ящике 8 белых и 13 красных шаров. Из ящика вынимают 2 шара. Найти вероятность того, что вынули: а) 2 белых шара, б) 1 белый и 1 красный шар. 2.13. В группе 30 учащихся. Из них 12 юношей, остальные девушки. Известно, что к доске должны быть вызваны двое учащихся. Какова вероятность того, что это девушки? 2.14. После бури на участке между 40 -м и 70 -м километрами телефонной линии произошёл обрыв провода. Какова вероятность того, что разрыв произошёл между 50 -м и 55 -м километрами линии? 2.15. В лифт семиэтажного дома на первом этаже вошли три человека. Каждый из них с одинаковой вероятностью выходит на любом этаже, начиная со второго. Найти вероятности следующих событий: А – все пассажиры выйдут на четвёртом этаже, В – все пассажиры выйдут на одном и том же этаже, С – все пассажиры выйдут на разных этажах.
2.16. При перевозке ящика, в котором содержалась 21 стандартная и 10 нестандартных деталей, утеряна одна деталь. Наудачу извлечённая (после перевозки) из ящика деталь оказалась стандартной. Найти вероятность этого события, при условии, что была утеряна: а) стандартная деталь, б) нестандартная деталь. 2.17. Бросают два игральных кубика. Найти вероятности следующих событий: А – произведение чисел очков равно 12, В – сумма квадратов чисел очков равна 25. 2.18. Монету бросают три раза. Какова вероятность того, что хотя бы два раза выпадет герб? 2.19. У ребёнка не умеющего читать, имеются буквы И, Н, Т, Е, Г, Р, А, Л. Какова вероятность того, что извлекая по очереди четыре буквы, он получит слово ТИГР? 2.20. В группе 15 юношей и 10 девушек. На вечер группа получила 5 билетов, которые разыгрываются по жребию. Какова вероятность того, что на вечер попадут 2 девушки и 3 юношей? ОПЕРАЦИИ НАД СОБЫТИЯМИ
Событие W называется достоверным, если осуществление эксперимента обязательно приводит к появлению этого события. Событие Событие А называется случайным, если в результате осуществления эксперимента оно может как произойти, так и не произойти. СуммойА+В событий А и В называется событие, состоящее в том, что произойдёт или А, или В, или оба вместе. ПроизведениемАВ событий А и В называется событие, состоящее в том, что произошли одновременно и А и В. События А и В называются несовместными, если Событие События
3.1. Рассмотрим события: А – хотя бы одно из группы изделий бракованное, В – бракованных изделий не менее двух. Что означают события 3.2. Событие В является частным случаем события А. Чему равны их сумма и произведение? 3.3. Монету бросают три раза. Под исходом опыта будем понимать последовательность 3.4. Мишень состоит из 10 кругов, ограниченных концентрическими окружностями с радиусами ri (i =1, 2,¼, 10), причём r1 < r2 <¼< r10. Событие Ai – попадание в круг радиуса ri. Что означают события 3.5. Пусть А, В, С – три произвольных события. Найти выражения для событий, состоящих в том, что из А, В, С: а) произошло только А; б) произошли А и В, но С не произошло; в) все три события произошли; г) произошло по крайней мере одно из этих событий; д) произошли по крайней мере два события; е) произошло одно и только одно событие; ж) произошли два и только два события; з) ни одно из событий не произошло; и) произошло не более двух событий. 3.6. Доказать, что события А, 3.7. Пусть А, В, С – случайные события. Выяснить смысл равенств: а) АВС = А, б) А+В+С = А. 3.8. Для сигнализации об аварии установлены два сигнализатора. Рассмотрим события: А – первый сигнализатор срабатывает при аварии, В – второй сигнализатор срабатывает при аварии. Используя операции над событиями, выразить через А и В события: С – при аварии срабатывает первый сигнализатор, D – при аварии срабатывает только один сигнализатор, Е – будет дан сигнал об аварии. 3.9. Пусть производится три выстрела по мишени. Событие Аi – попадание при i -ом выстреле. Выразить через события Аi следующие события: В – хотя бы одно попадание, С – ни одного попадания, D – только одно попадание, Е – только два попадания, F – не менее двух попаданий. 3.10. Будут ли равными события А и В, если а)
ФОРМУЛА БЕРНУЛЛИ
Если в каждом из n независимых испытаний вероятность появления события А одна и та же и равна p, то вероятность того, что в n испытаниях событие А появится k раз, находится по формуле Бернулли
6.1. Вероятность того, что расход электроэнергии за рабочий день на механическом заводе не будет превышать нормы равна 0,75. Найти вероятность того, что среди 6 рабочих дней окажется 2 дня, в течение которых произойдёт перерасход электроэнергии. 6.2. Производится 5 независимых выстрелов в одинаковых условиях. Вероятность попадания при каждом выстреле равна 0,8. Найти вероятность того, что будет более одного попадания. 6.3. Два спортсмена играют в настольный теннис. Вероятность выигрыша первого спортсмена равна 6.4. Считая вероятности рождения человека по временам года одинаковыми, найти вероятность того, что из 6 человек не менее 5 родились зимой? 6.5. Производится 8 выстрелов по резервуару с горючим, причём первое попадание вызывает течь, а второе – воспламенение горючего. Какова вероятность того, что резервуар будет подожжен, если вероятность попадания при отдельном выстреле равна 0,2? 6.6. Отрезок АВ разделён точкой С в отношении 2:1. На этот отрезок наудачу «брошены» 4 точки. Найти вероятность того, что две из них окажутся левее точки С и две – правее. Предполагается, что вероятность попадания точки на отрезок пропорциональна длине отрезка и не зависит от его расположения. 6.7. Система радиолокационных станций ведёт наблюдение за группой из 6.8. В случайно выбранной семье четверо детей. Считая вероятности рождения мальчика и девочки одинаковыми, определить вероятность того, что в выбранной семье окажется: а) два мальчика и две девочки, б) более двух мальчиков. 6.9. Что вероятнее выиграть у равносильного противника: а) 3 партии из 4 или 5 из 8, б) не менее 3 партий из 4 или не менее 5 из 8? 6.10. Всхожесть семян данного сорта растений оценивается вероятностью равной 0,8. Какова вероятность того, что из пяти посеянных семян взойдут не менее четырёх?
ЭЛЕМЕНТЫ ТЕОРИИ СТРУКТУРНОЙ НАДЁЖНОСТИ
Надёжностью изделия в широком смысле называется способность изделия сохранять качество в течение определённого периода эксплуатации. Математической надёжностью изделия за время t называется вероятность его безотказной работы за это время. Для анализа надёжности составляется структурная схема изделия. При этом различают последовательное и параллельное соединения элементов системы в смысле надёжности. Последовательным называется такое соединение элементов в системе, при котором отказ любого из них приводит к отказу системы. При последовательном соединении надёжность системы P выражается через надёжности элементов Параллельным называется такое соединение элементов в системе, при котором отказ системы наступает только при отказе всех её элементов. При параллельном соединении надёжность системы P выражается по формуле
7.1. Система состоит из трёх элементов, отказы которых независимы, а вероятности отказов равны 0,1, 0,2, 0,3. Для отказа системы достаточно, чтобы отказал любой из её элементов. Найти надёжность системы. 7.2. Система состоит из трёх элементов, отказы которых независимы, а вероятности отказов равны 0,2, 0,1, 0,5. Отказ системы наступает тогда, когда отказывают все три элемента. Найти надёжность системы. 7.3. Определить надёжность системы.
Надёжности элементов равны: p1 = 0,8; p2 = 0,7; p3 = 0,9; p4 = 0,6.
7.4. Определить надёжность системы.
Надёжности элементов равны: p1 = 0,8; p2 = 0,9; p3 = 0,7; p4 = 0,6; p5 = 0,5.
7.5. Определить надёжность системы.
Надёжности элементов равны: p1 = 0,7; p2 = 0,8; p3 = 0,6; p4 = 0,7; p5 = 0,8.
7.6. Прибор состоит из двух узлов, отказы которых независимы, и выходит из строя, если откажет хотя бы один узел. Вероятность безотказной работы первого узла в течение времени t равна 0,8, второго – 0,7. Прибор испытывался в течение времени t, в результате чего он вышел из строя. Найти вероятность того, что отказал только первый узел. 7.7. Система испытывалась в течение времени t, в результате чего она вышла из строя. Найти вероятность того, что отказали только элементы с номерами 2 и 4.
Надёжности элементов равны: p1 = 0,6; p2 = 0,8; p3 = 0,7; p4 = 0,9.
7.8. Система состоит из пяти элементов, отказы которых независимы, а вероятности отказов за время t одинаковы и равны 0,3. Отказ системы наступает лишь тогда, когда выходят из строя по меньшей мере три элемента из пяти. Найти надёжность системы за время t. 7.9. Прибор может работать в двух режимах: нормальном и с перегрузкой. Нормальный режим наблюдается в 80 % всех случаев включения прибора. Вероятность выхода из строя за время t в нормальном режиме равна 0,1, в режиме с перегрузкой – 0,7. Определить надёжность прибора за время t. 7.10. В прибор входят 3 одинаковых лампы, вероятность перегорания каждой из которых равна 0,3 и перегорания независимы. Если перегорит только одна лампа, то прибор выходит из строя с вероятностью 0,4, только две – с вероятностью 0,7. Если перегорят все лампы, то прибор обязательно выйдет из строя. Найти вероятность того, что прибор выйдет из строя.
7.11. Определить надёжность системы.
Надёжности элементов равны: p1 = 0,7; p2 = 0,8; p3 = 0,6; p4 = 0,7; p5 = 0,9; p6 = 0,9.
7.12. Прибор состоит из двух узлов, отказы которых независимы, и выходит из строя, если откажет хотя бы один узел. Вероятность безотказной работы первого узла в течение времени t равна 0,8, второго – 0,7. Прибор испытывался в течение времени t, в результате чего он вышел из строя. Найти вероятность того, что отказали оба узла. 7.13. Определить надёжность системы.
Надёжности элементов равны: p1 = 0,9; p2 = 0,9; p3 = 0,8; p4 = 0,8; p5 = 0,7.
7.14. Изделие можно разбить на три блока, отказы которых за время t независимы, а вероятности отказов равны соответственно 0,2, 0,3, 0,1. Найти надёжность изделия в следующих случаях: а) изделие выходит из строя, если отказывает хотя бы один из трёх выделенных блоков; б) изделие выходит из строя лишь тогда, когда отказывают все три блока; в) для выхода изделия необходимо, чтобы вышли из строя по меньшей мере два из трёх блоков. 7.15. Система испытывалась в течение времени t, в результате чего она вышла из строя. Найти вероятность того, что отказали только элементы с номерами 2 и 5.
Надёжности элементов равны: p1 = 0,9; p2 = 0,8; p3 = 0,5; p4 = 0,4; p5 = 0,7.
СЛУЧАЙНЫЕ ВЕЛИЧИНЫ Случайнойвеличиной называется величина, которая в результате эксперимента может принять то или иное значение, заранее неизвестно какое. Закономраспределения случайной величины называется всякое соотношение, устанавливающее связь между возможными значениями случайной величины и соответствующими им вероятностями. Функцияраспределения случайной величины Х обозначается F(x) и определяется равенством P { X<x }. Свойства функции распределения: 1) 0 £ F(x) £ 1; 2) F(x1)£F(x2), если x1£x2; 3) 4) F(x) непрерывна слева: Вероятность попадания случайной величины Х на числовой промежуток [ a; b ) вычисляется по формуле БИНОМИАЛЬНОЕ РАСПРЕДЕЛЕНИЕ
Дискретная случайная величина Х называется биномиальной с параметрами Математическое ожидание и дисперсия биноминальной случайной величины выражается через её параметры следующим образом:
10.1. Случайная величина X распределена биномиально с параметрами n = 4, p = 0,5. Найти Р { 0,5 £ X £ 2,5 }. 10.2. Вероятность выигрыша в лотерею по одному лотерейному билету равна 0,05. Найти математическое ожидание и дисперсию числа лотерейных билетов, на которые выпадают выигрыши, если приобретено 40 билетов. 10.3. В партии 90% стандартных деталей. Наудачу отобраны четыре детали. Написать закон распределения дискретной случайной величины Х – числа нестандартных деталей среди четырёх отобранных. 10.4. Найти дисперсию дискретной случайной величины Х – числа появления события А в двух независимых испытаниях, если вероятности появления события в этих испытаниях одинаковы и известно, что M[X] = 0,9. 10.5. Завод изготавливает 80% изделий первого сорта и 20% второго. Найти математическое ожидание, дисперсию и среднее квадратическое отклонение числа изделий первого сорта в партии из 1000 отобранных случайным образом изделий.
10.6. Найти постоянную вероятность попадания в цель при каждом выстреле и число произведённых выстрелов, если среднее число попаданий равно 72, а среднее квадратическое отклонение случайной величины, характеризующей число попаданий, равно 6. 10.7. Два игральных кубика одновременно бросают два раза. Написать закон распределения случайной величины Х – числа выпадения чётного числа очков на двух игральных кубиках. 10.8. Вероятность того, что лампа остается исправной после 1000 часов работы, равна 0,2. Написать закон распределения случайной величины Х – числа неисправных ламп после 1000 часов работы из трех имеющихся. Найти числовые характеристики данной случайной величины. РАСПРЕДЕЛЕНИЕ ПУАССОНА. ПРОСТЕЙШИЙ ПОТОК СОБЫТИЙ
Дискретная случайная величина Х называется пуассоновской с параметром Математическое ожидание и дисперсия пуассоновской случайной величины выражается через параметр l следующим образом:
Пуассоновская случайная величина является предельным случаем биномиальной случайной величины при Потоком событий называют последовательность событий, происходящих в случайные моменты времени. Простейшим ( пуассоновским ) называют поток событий, обладающий свойствами стационарности, отсутствия последействия и ординарности. Свойство стационарности состоит в том, что вероятность появления k событий в любом промежутке времени зависит только от числа k и от длительности t промежутка времени и не зависит от расположения на оси. Свойство отсутствия последействия состоит в том, что вероятность появления k событий в любом промежутке времени не зависит от того, появлялись или не появлялись события в моменты времени, предшествующие началу рассматриваемого промежутка. Свойство ординарности состоит в том, что появление двух и более событий за малый промежуток времени практически невозможно. Интенсивностью потока l называют среднее число событий, которые появляются в единицу времени. Если постоянная интенсивность потока l известна, то вероятность появления k событий простейшего потока за время t определяется формулой Пуассона:
11.1. Случайная величина X распределена по закону Пуассона с параметром l = 3. Найти Р { 0,5 £ X £ 2,5 }. 11.2. Станок-автомат штампует детали. Вероятность того, что изготовленная деталь окажется бракованной, равна 0,01. Найти вероятность того, что среди 200 деталей окажется ровно 4 бракованных. 11.3. Средняя плотность болезнетворных микробов в одном кубическом метре воздуха равна 100. Берётся на пробу 20 дм3 воздуха. Найти вероятность того, что в нём будет обнаружен хотя бы один микроб. 11.4. На ремонтную базу поступает в среднем 16 заявок в день (рабочий день восьмичасовой). Поток заявок можно считать простейшим. Найти вероятность того, что а) за один час не поступит ни одной заявки; б) за два часа поступит не менее двух и не более трёх заявок. 11.5. Поток неисправностей (сбоев), возн
|
||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 529; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.126.69 (0.02 с.) |


 Брянский государственный технический университет
Брянский государственный технический университет
 . Бумага офсетная. Офсетная печать. Подписано в печать
Усл. печ. л. 3,42 Уч.-изд. л. 3,42 Тираж 200 экз. Заказ Бесплатно.
. Бумага офсетная. Офсетная печать. Подписано в печать
Усл. печ. л. 3,42 Уч.-изд. л. 3,42 Тираж 200 экз. Заказ Бесплатно.
 .
. .
.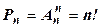 .
. }, определяется равенством
}, определяется равенством , где
, где  .
. .
. .
. , где n – общее число произведённых экспериментов,
, где n – общее число произведённых экспериментов,  – число экспериментов, в которых наступило событие А.
– число экспериментов, в которых наступило событие А.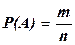 .
. называется невозможным, если осуществление эксперимента никогда не приводит к его появлению.
называется невозможным, если осуществление эксперимента никогда не приводит к его появлению.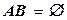 .
. называется противоположным событию А, если
называется противоположным событию А, если  и
и  .
. образуют полную группу событий, если
образуют полную группу событий, если  (i¹j) и
(i¹j) и  .
.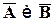 ?
? , где каждая
, где каждая  обозначает выпадения герба (Г) или цифры (Ц). Построить пространство элементарных событий. Описать событие А, состоящее в том, что выпало не менее двух гербов.
обозначает выпадения герба (Г) или цифры (Ц). Построить пространство элементарных событий. Описать событие А, состоящее в том, что выпало не менее двух гербов. ,
,  ?
? и
и  образуют полную группу событий.
образуют полную группу событий. , б) для некоторого события С: А + С = В + С, в) для любого события С: А + С = В + С?
, б) для некоторого события С: А + С = В + С, в) для любого события С: А + С = В + С?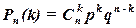 , где
, где  .
. . Какова вероятность того, что он выиграет 2 партии из 5?
. Какова вероятность того, что он выиграет 2 партии из 5? по формуле
по формуле  .
.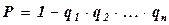 , где
, где  .
.





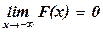 ,
,  ;
; .
. .
. , где
, где  .
. ;
;  .
.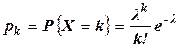 .
. .
. , так, что
, так, что  , где l – постоянная величина.
, где l – постоянная величина.




