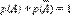Классическое определение вероятности. Свойства вероятности.

Случайные события

Событием (случайным событием) называется всякий факт, который может произойти или не произойти в результате опыта. События обозначаются буквами А, B, C, D, … Вероятностью события называется численная мера возможности появления события в результате данного опыта. Вероятность события А обозначается Р(А). Событие W, которое обязательно произойдет в результате опыта, называется достоверным: Р(W) = 1. Событие Æ, которое никогда не может произойти в результате опыта, называется невозможным: Р(Æ) = 0. Событие А, о котором нельзя заранее сказать произойдет оно или нет в результате опыта, называется случайным: 0£Р(А)£1. Суммой событий А+В называется событие, состоящее в осуществлении хотя бы одного из событий А или В (безразлично, какого именно, или обоих, если это возможно).

Классическое определение вероятности. Свойства вероятности.

Пусть в результате опыта может произойти одно из n элементарных событий, причем событию А благоприятствуют m из них (m£n). Тогда вероятностью события А называется отношение числа элементарных исходов, благоприятствующих появлению события А, к общему числу равновозможных элементарных исходов: Р(А)= m/n.

Нормировка вероятности: 0 ≤ p (A) ≤ 1 для любого события A

Вероятность противоположного события:

Для независимых событий A и B: p (A и B) = p (A) p (B), p (A или B) = p (A) + p (B)

Условная вероятность: p (AB) = p (B) · p (A | B)

Формула полной вероятности: p (B) = p (B | A1) p (A1) + p (B | A2) p (A2) + p (B | A3) p (A3) +… + p (B | Ak) p (Ak)

3. Алгебра событий:. Суммой А+В двух событий А и В называют событие, состоящее в том, что произошло хотя бы одно из событий А и В. Суммой нескольких событий, соответ-ственно, называется событие, заключающееся в том, что произошло хотя бы одно из этих событий. Произведением АВ событий А и В называется событие, состоящее в том, что произошло и событие А, и событие В. Аналогично произведением нескольких событий называется событие, заключающееся в том, что произошли все эти события. Разностью А\B событий А и В называется событие, состоящее в том, что А произошло, а В – нет. События А и В называются совместными, если они могут произойти оба в результате одного опыта. В противном случае (то есть если они не могут произойти одновременно) события называются несовместными.

4. Основные формулы комбинаторики. Комбинаторика изучает количества комбинаций, подчиненных определенным условиям, которые можно составить из элементов, безразлично какой природы, заданного конечного множества. При непосредственном вычислении вероятностей часто используют формулы комбинаторики. Приведем наиболее употребительные из них. Перестановками называют комбинации, состоящие из одних и тех же n различных элементов и отличающиеся только порядком их расположения. Число всех возможных перестановок Pn = n!, где n! = 1 * 2 * 3... n. Размещениями называют комбинации, составленные из n различных элементов по m элементов, которые отличаются либо составом элементов, либо их порядком. Число всех возможных размещений Amn = n (n - 1)(n - 2)... (n - m + 1). Сочетаниями называют комбинации, составленные из n различных элементов по m элементов, которые отличаются хотя бы одним элементом. Число сочетаний С mn = n! / (m! (n - m)!).

Подчеркнем, что числа размещений, перестановок и сочетаний связаны равенством Amn = PmC mn.

Сумма событий. Вероятность суммы несовместимых событий.

Суммой А + В двух событий А и В называют событие, состоящее в появлении события А, или события В, или обоих этих событий. Например, если из орудия произведены два выстрела и А — попадание при первом выстреле, В — попадание при втором выстреле, то А + В — попадание при первом выстреле, или при втором, или в обоих выстрелах. Суммой нескольких событий называют событие, которое состоит в появлении хотя бы одного из этих событий. Например, событие А + В + С состоит в появлении одного из следующих событий: А, В, С, А и В, А и С, В и С, А и В и С. Пусть события A и В — несовместные, причем вероятности этих событий известны. Как найти вероятность того, что наступит либо событие A, либо событие В? Ответ на этот вопрос дает теорема сложения. Вероятность появления одного из двух несовместных событий, безразлично какого, равна сумме вероятностей этих событий: Р (А + В) = Р (А) + Р (В). Вероятность появления одного из нескольких попарно несовместных событий, безразлично какого, равна сумме вероятностей этих событий:Р (A1 + A2 +... + An) = Р (A1) + Р (A2) +... + Р (An).

Свойства математического ожидания дискретной случайной величины.

1)Математическое ожидание постоянной величины равно самой постоянной: M(C) = C.

2) Постоянный множитель можно выносить за знак математического ожидания: M(CX) = CM(X).

3) Математическое ожидание суммы нескольких случайных величин равно сумме математических ожиданий слагаемых: M(X+Y+Z) = M(X)+M(Y)+M(Z).

4) Математическое ожидание произведения нескольких взаимно независимых случайных величин равно произведению их математических ожиданий: M(X*Y*Z) = M(X)*M(Y)*M(Z). Все эти свойства имеют большое практическое значение.

14. Отклонение случайной величины.

Случайные события

Событием (случайным событием) называется всякий факт, который может произойти или не произойти в результате опыта. События обозначаются буквами А, B, C, D, … Вероятностью события называется численная мера возможности появления события в результате данного опыта. Вероятность события А обозначается Р(А). Событие W, которое обязательно произойдет в результате опыта, называется достоверным: Р(W) = 1. Событие Æ, которое никогда не может произойти в результате опыта, называется невозможным: Р(Æ) = 0. Событие А, о котором нельзя заранее сказать произойдет оно или нет в результате опыта, называется случайным: 0£Р(А)£1. Суммой событий А+В называется событие, состоящее в осуществлении хотя бы одного из событий А или В (безразлично, какого именно, или обоих, если это возможно).

Классическое определение вероятности. Свойства вероятности.

Пусть в результате опыта может произойти одно из n элементарных событий, причем событию А благоприятствуют m из них (m£n). Тогда вероятностью события А называется отношение числа элементарных исходов, благоприятствующих появлению события А, к общему числу равновозможных элементарных исходов: Р(А)= m/n.

Нормировка вероятности: 0 ≤ p (A) ≤ 1 для любого события A

Вероятность противоположного события:

Для независимых событий A и B: p (A и B) = p (A) p (B), p (A или B) = p (A) + p (B)

Условная вероятность: p (AB) = p (B) · p (A | B)

Формула полной вероятности: p (B) = p (B | A1) p (A1) + p (B | A2) p (A2) + p (B | A3) p (A3) +… + p (B | Ak) p (Ak)

3. Алгебра событий:. Суммой А+В двух событий А и В называют событие, состоящее в том, что произошло хотя бы одно из событий А и В. Суммой нескольких событий, соответ-ственно, называется событие, заключающееся в том, что произошло хотя бы одно из этих событий. Произведением АВ событий А и В называется событие, состоящее в том, что произошло и событие А, и событие В. Аналогично произведением нескольких событий называется событие, заключающееся в том, что произошли все эти события. Разностью А\B событий А и В называется событие, состоящее в том, что А произошло, а В – нет. События А и В называются совместными, если они могут произойти оба в результате одного опыта. В противном случае (то есть если они не могут произойти одновременно) события называются несовместными.

4. Основные формулы комбинаторики. Комбинаторика изучает количества комбинаций, подчиненных определенным условиям, которые можно составить из элементов, безразлично какой природы, заданного конечного множества. При непосредственном вычислении вероятностей часто используют формулы комбинаторики. Приведем наиболее употребительные из них. Перестановками называют комбинации, состоящие из одних и тех же n различных элементов и отличающиеся только порядком их расположения. Число всех возможных перестановок Pn = n!, где n! = 1 * 2 * 3... n. Размещениями называют комбинации, составленные из n различных элементов по m элементов, которые отличаются либо составом элементов, либо их порядком. Число всех возможных размещений Amn = n (n - 1)(n - 2)... (n - m + 1). Сочетаниями называют комбинации, составленные из n различных элементов по m элементов, которые отличаются хотя бы одним элементом. Число сочетаний С mn = n! / (m! (n - m)!).

Подчеркнем, что числа размещений, перестановок и сочетаний связаны равенством Amn = PmC mn.

Познавательные статьи:



Техника прыжка в длину с разбега

Организация работы процедурного кабинета

Области применения синхронных машин

Оптимизация по Винеру и Калману