Алгоритмы устранения геометрических искажений

 

2.4.1 Алгоритмы отсечения

 

Отсечение – это удаление той части изображения, которая не попадает в заданное окно на экране монитора. В качестве окна могут приниматься: окно дисплея, графическое окно программы, другие произвольные контуры. Необходимость выполнения отсечения связана с тем, что некоторые, в основном, простые дисплеи не допускают выхода изображения за пределы экрана, а также, в связи с широким использованием технологии просмотра окнами, требующим выполнения отсечения сцены по границам окна видимости, так как выход за пределы окна приводит к искажению картины.

Графическая задача отсечения в обобщенном виде заключается в вычислении точек пересечения отрезков, из которых составлено изображение, с ограничивающими линиями окна отсечения, определении новых координат концов для этих отрезков и прорисовки изображения с помощью этих новых отрезков.

Отсекаемые отрезки могут быть трех классов - целиком видимые, целиком невидимые и пересекающие окно. Очевидно, что принятие решения о видимости целиком или отбрасывании отрезка надо делать в первую очередь. По способу выбора решения об отбрасывании невидимого отрезка существует два основных типа алгоритмов отсечения - алгоритмы, использующие кодирование концов отрезка или всего отрезка и алгоритмы, использующие параметрическое представление отсекаемых отрезков и окна отсечения.

К алгоритмам первого типа (с кодированием концов отрезков) относятся - алгоритм Коэна-Сазерленда (Cohen-Sutherland, CS-алгоритм) и FC-алгоритм (Fast Clipping - алгоритм).

К алгоритмам второго типа (параметрическим) относятся - алгоритм Кируса-Бека (Curus-Beck, CB - алгоритм) и алгоритм Лианга-Барски (Liang-Barsky, LB-алгоритм).

Алгоритмы с кодированием применимы для прямоугольного окна, стороны которого параллельны осям координат, в то время как алгоритмы с параметрическим представлением применимы для произвольного окна.

Алгоритм Коэна-Сазерленда является стандартом де-факто алгоритмов отсечения линий и обладает одним из лучших быстродействием при компактной реализации.

FC-алгоритм - наиболее быстрый, но и чрезвычайно громоздкий.

Алгоритм Лианга-Барски применяется для отсечения прямоугольным окном с использованием параметрического представления. Быстродействие этого алгоритма сравнимо с быстродействием алгоритма Коэна-Сазерленда при большей компактности и наличии 3D и 4D реализаций.

Алгоритм Кируса-Бека использует параметрическое представление и позволяет отсекать произвольным выпуклым окном.

Программное исполнение отсечения достаточно медленный процесс, поэтому, в мощные дисплеи встраивается соответствующая аппаратура. Впервые аппаратура отсечения, использующая алгоритм отсечения делением отрезка пополам была реализована в устройстве Clipping Divider, в 1968 г.

Здесь мы рассмотрим программную реализацию алгоритма отсечения Коэна-Сазерленда [10].

Этот алгоритм позволяет быстро выявить отрезки, которые могут быть либо приняты, либо отброшены целиком. Вычисление пересечений требуется, когда отрезок не попадает ни в один из этих классов.

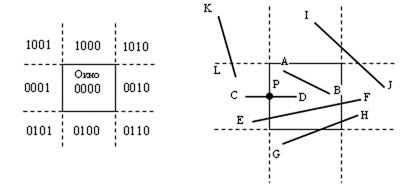
Рисунок 2.13 – Отсечение по методу Коэна-Сазерленда

 

Идея алгоритма состоит в следующем:

1) Окно отсечения и прилегающие к нему части плоскости вместе образуют 9 областей, которым присваиваются 4-х разрядные коды (рис. 2.13).

Две конечные точки отрезка получают 4-х разрядные коды, соответствующие областям, в которые они попали.

2) Определение положения отрезка, либо целиком внутри окна, либо целиком вне окна выполняется следующим образом:

- если коды концов отрезка: Код1=0 и Код2=0 то - отрезок целиком внутри окна, он принимается как видимый (отрезок AB);

- если (Код1 & Код2) ¹ 0 - то отрезок целиком вне окна, он принимается как невидимый (отрезок KL);

- если (Код1 & Код2) = 0 - то отрезок может быть частично видимым (отрезки CD, EF, GH) или целиком невидимым (отрезок IJ); для него нужно определить координаты пересечений со сторонами окна и для каждой полученной части определить тривиальную видимость или невидимость. При этом для отрезков CD и IJ потребуется вычисление одного пересечения, для остальных (EF и GH) - двух.

При расчете пересечения используется горизонтальность либо вертикальность сторон окна, что позволяет определить координату X или Y точки пересечения без вычислений [9].

При непосредственном использовании описанного выше способа отбора целиком видимого или целиком невидимого отрезка после расчета пересечения потребовалось бы вычисление кода расположения точки пересечения. Для примера рассмотрим отрезок CD. Точка пересечения обозначена как P. В силу того, что граница окна считается принадлежащей окну, то можно просто принять только часть отрезка PD, попавшую в окно. Часть же отрезка CP, на самом деле оказавшаяся вне окна, потребует дальнейшего рассмотрения, так как логическое И кодов точек C и P даст 0, т.е. отрезок CP нельзя просто отбросить. Для решения этой проблемы Коэн и Сазерленд предложили заменять конечную точку с ненулевым кодом конца на точку, лежащую на стороне окна, либо на ее продолжении.

В целом схема алгоритма Коэна-Сазерленда следующая:

1. Рассчитать коды конечных точек отсекаемого отрезка.

2. В цикле повторять пункты 2-6.

3. Если логическое И кодов конечных точек не равно 0, то отрезок целиком вне окна. Он отбрасывается и отсечение закончено.

4. Если оба кода равны 0, то отрезок целиком видим. Он принимается и отсечение закончено.

5. Если начальная точка внутри окна, то она меняется местами с конечной точкой.

6. Анализируется код начальной точки для определения стороны окна, с которой есть пересечение и выполняется расчет пересечения. При этом вычисленная точка пересечения заменяет начальную точку.

7. Определение нового кода начальной точки [8].

 

2.4.2 Алгоритмы заполнения и заливки

 

Заполнение – это закраска внутренней части многоугольника в режиме сканирования строк. Многоугольник задается координатами его вершин.

Заливка – это закраска определенной области в режиме затравочного заполнения. Заливаемая область определяется по коду пикселев, расположенных внутри этой области. Если код пикселя отличается от кода так называемого затравочного пикселя, значит он находится снаружи заливаемой области.

Основное отличие заполнения многоугольника от заливки области состоит в следующем:

При заполнении многоугольника информация о предельных размерах части экрана, занятой многоугольником задается сразу, с помощью координат вершин заполняемой области.

При заливке области вначале надо прочитать текущий пиксель, затем определить по его цвету, принадлежит ли он заливаемой области и если принадлежит, то перекрасить.

 

 

2.4.3 Алгоритмы заполнения

 

Различают два вида заполнения: простое и построчное.

Простой алгоритм заполнения заключается в определении, принадлежит ли текущий пиксель внутренней части многоугольника. Если принадлежит, то пиксель заносится.

Определить принадлежность пикселя многоугольнику можно, например, подсчетом суммарного угла с вершиной на пикселе при обходе контура многоугольника. Если пиксель внутри, то угол будет равен 360^°, если вне - 0^° (рис. 2.13).

 

Рисунок 2.13 – Определение принадлежности пикселя многоугольнику

 

Вычисление принадлежности должно производиться для всех пикселев экрана и так как большинство пикселев скорее всего вне многоугольников, то данный способ слишком расточителен. Объем лишних вычислений в некоторых случаях можно сократить использованием прямоугольной оболочки - минимального прямоугольника, объемлющего интересующий объект, но все равно вычислений будет много [12].

Другой метод определения принадлежности точки внутренней части многоугольника используется в алгоритме Кируса-Бека.

 

2.4.4 Алгоритм построчного заполнения

 

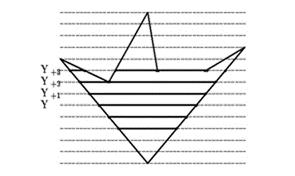
Реально используются алгоритмы построчного заполнения, основанные на том, что соседние пиксели в строке скорее всего одинаковы и меняются только там где строка пересекается с ребром многоугольника. Это называется когерентностью растровых строк (строки сканирования Y_i, Y_i+1, Y_i+2 на рис.2.14). При этом достаточно определить X-координаты пересечений строк сканирования с ребрами. Пары отсортированных точек пересечения задают интервалы заливки [8].

 

Рисунок 2.14 –Построчное заполнение многоугольника

 

Кроме того, если какие-либо ребра пересекались i-й строкой, то они скорее всего будут пересекаться также и строкой i+1. (строки сканирования Y_i и Y_i+1 на рис.2.14). Это называется когерентностью ребер. При переходе к новой строке легко вычислить новую X-координату точки пересечения ребра, используя X-координату старой точки пересечения и тангенс угла наклона ребра:

 

X_i+1 = X_i + 1/k

 

Тангенс угла наклона ребра: k = dy/dx,

так как dy = 1, то: 1/k = dx

 

Смена же количества интервалов заливки происходит только тогда, когда в строке сканирования появляется вершина.

Учет когерентности строк и ребер позволяет построить для заполнения многоугольников различные высокоэффективные алгоритмы построчного сканирования. Для каждой строки сканирования рассматриваются только те ребра, которые пересекают строку [13]. Они задаются списком активных ребер (САР). При переходе к следующей строке для пересекаемых ребер перевычисляются X-координаты пересечений. При появлении в строке сканирования вершин производится перестройка САР. Ребра, которые перестали пересекаться, удаляются из САР, а все новые ребра, пересекаемые строкой заносятся в него.

 

Рисунок 2.15 – Сравнение алгоритмов заполнения многоугольника

 

В отличие от V_FP0, в программе V_FP1 используется более сложный алгоритм формирования САР, обеспечивающий практически полное отсутствие дублирований (рис. 2.15).

 

2.4.5 Алгоритмы заливки

 

В алгоритмах заливки задается заливаемая (перекрашиваемая) область, код пиксела, которым будет выполняться заливка и начальная точка в области, начиная с которой начнется заливка.

Виды заливок:

- простой алгоритм заливки с затравкой;

- построчный алгоритм заливки с затравкой.

 

По способу задания области заливки делятся на два типа:

1) Гранично-определенные, задаваемые своей (замкнутой) границей такой, что коды пикселев границы отличны от кодов внутренней, перекрашиваемой части области. На коды пикселев внутренней части области налагаются два условия - они должны быть отличны от кода пикселев границы и кода пикселя перекраски. Если внутри гранично-определенной области имеется еще одна граница, нарисованная пикселями с тем же кодом, что и внешняя граница, то соответствующая часть области не должна перекрашиваться;

2) Внутренне-определенные, нарисованные одним определенным кодом пикселя. При заливке этот код заменяется на новый код закраски.

По способам доступа к соседним пикселям области делятся на 4-х и 8-ми связные.

В 4-х связных областях доступ к соседним пикселям осуществляется по четырем направлениям - горизонтально влево и вправо и в вертикально вверх и вниз.

В 8-ми связных областях к этим направлениям добавляются еще 4 диагональных. Используя связность мы может, двигаясь от точки затравки, достичь и закрасить все пиксели области [20].

4-х связную область мы можем заполнить как 4-х, так и 8-ми связным алгоритмом. Обратное же неверно. Так, область на рис.2.16.(а) мы можем заполнить любым алгоритмом, а область на рис.2.16. (б), состоящую из двух примыкающих 4-х связных областей можно заполнить только 8-ми связным алгоритмом.

С использованием связности областей и стека можно построить простые алгоритмы закраски как внутренне, так и гранично-определенной области.

Рисунок.2.16.– Связность областей и их границ

 

Простой алгоритм заливки может быть выполнен двумя способами:

- в рекурсивной реализации;

- в итеративной реализации.

Алгоритм заливки в рекурсивной реализации гранично-определенной 4-х связной области выполняется в следующем порядке:

- определяется, является ли пиксель граничным или уже закрашенным;

- если нет, то пиксель перекрашивается, затем проверяются и если надо перекрашиваются 4 соседних пикселя.

Несмотря на простоту, рекурсивная реализация проигрывает итеративной в том, что требуется много памяти для сохранения вложенных вызовов.

Логика работы итеративного алгоритма заливки 4-х связной гранично-определенной области следующая:

1. Поместить координаты затравки в стек;

2. Если стек не пуст, извлечь из него координаты пикселя;

3. Перекрасить пиксель;

4. Для всех четырех соседних пикселев проверить, является ли он граничным или уже перекрашен;

5. Если нет, то занести его координаты в стек.

 

На рис.2.17 (а) показан выбранный порядок перебора соседних пикселев, а на рис.2.17 (б) соответствующий ему порядок закраски простой гранично-определенной области.

 

 

Рисунок 2.17. – Заливка 4-х связной области итеративным алгоритмом

Как уже отмечалось, очевидный недостаток алгоритмов непосредственно использующих связность закрашиваемой области - большие затраты памяти на стек, так как на каждый закрашенный пиксель в стеке по максимуму будет занесена информация о еще трех соседних. Кроме того, информация о некоторых пикселях может записываться в стек многократно. Это приведет не только к перерасходу памяти, но и потере быстродействия за счет многократной раскраски одного и того же пикселя. Значительно более экономен далее рассмотренный построчный алгоритм заливки.

Построчный алгоритм заливки.

Использует пространственную когерентность, при которой:

- пиксели в строке меняются только на границах;

- при перемещении к следующей строке размер заливаемой строки скорее всего или неизменен или меняется на 1 пиксель.

Таким образом, на каждый закрашиваемый фрагмент строки в стеке хранятся координаты только одного начального пикселя, что приводит к существенному уменьшению размера стека.

Последовательность работы алгоритма для гранично-определенной области следующая:

1. Координата затравки помещается в стек, затем до исчерпания стека выполняются пункты 2-4.

2. Координата очередной затравки извлекается из стека и выполняется максимально возможное закрашивание вправо и влево по строке с затравкой, т.е. пока не попадется граничный пиксель. Пусть это Хлев и Хправ, соответственно.

3. Анализируется строка ниже закрашиваемой в пределах от Хлев до Хправ и в ней находятся крайние правые пикселы всех незакрашенных фрагментов. Их координаты заносятся в стек.

4. То же самое проделывается для строки выше закрашиваемой [16].

В результате проведенного анализа алгоритмов поиска кратчайшего пути основой для разработки автоматизированной системы прокладки интернет кабелей был выбран алгоритм Дейкстры, потому как он наиболее точнее и быстрее справляется с поставленной задачей. Также был проведен структурный анализ данных, в ходе которого были построены следующие диаграммы: диаграмма потоков данных, диаграмма состояний и контекстная диаграмма на основе созданной математической модели [18].