
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Перестановки с повторениями.Размещение без повторений Размещения без повторений — комбинаторные соединения, составленные из n элементов по m. При этом два соединения считаются различными, если они либо отличаются друг от друга хотя бы одним элементом, либо состоят из одних и тех же элементов, но расположенных в разном порядке. формула для нахождения количества размещений без повторений:
формула для нахождения количества размещений с повторениями: Перестановки. В комбинаторике перестано́вка — это упорядоченный набор чисел Свойства: Число всех перестановок порядка
Композиция определяет операцию произведения на перестановках одного порядка: Любая группа является подгруппой группы перестановок множества элементов этой группы (теорема Кэли). При этом каждый элемент Сочетания. В комбинаторике сочетанием из Так, например, наборы (3-хэлементные сочетания, подмножества, В общем случае число, показывающее, сколькими способами можно выбрать Сочетания с повторениями. Сочетанием с повторениями называются наборы, в которых каждый элемент может участвовать несколько раз. Число сочетаний с повторениями из
При фиксированном
Двумерной производящей функцией чисел сочетаний с повторениями является:
Бином Ньютона. Бино́м Нью́то́на — формула для разложения на отдельные слагаемые целой неотрицательной степени суммы двух переменных, имеющая вид
где В таком виде эта формула была известна ещё индийским и исламским математикам; Ньютон вывел формулу бинома для более общего случая, когда показатель степени — произвольное рациональное число (возможно, отрицательное). В этом случае бином представляет собой бесконечный ряд Свойства бинома Ньютона Разложение бинома (a + b)n представляет собой многочлен, расположенный по убывающим степеням a (от n-й до нулевой) и по возрастающим степеням b (от нулевой до n-й); сумма показателей a и b в каждом члене разложения равна показателю степени бинома. Число членов разложения на единицу больше показателя степени бинома. Коэффициенты членов разложения («биноминальные коэффициенты») возрастают до середины разложения и затем убывают; коэффициенты каждой пары членов, равноотстоящих от начала и конца разложения, равны между собой. Если n четное, то имеется один средний наибольший коэффициент; если n нечетное, то имеется два средних наибольших коэффициента. При возведении в n-ю степень разности a - b все четные члены разложения имеют знак "минус": Треугольник Паскаля. Треугольник Паскаля — бесконечная таблица биномиальных коэффициентов, имеющая треугольную форму. В этом треугольнике на вершине и по бокам стоят единицы. Каждое число равно сумме двух расположенных над ним чисел. Строки треугольника симметричны относительно вертикальной оси. Назван в честь Блеза Паскаля. Свойства Числа треугольника симметричны(равны) относительно вертикальной оси. В строке с номером n: первое и последнее числа равны 1. второе и предпоследнее числа равны n. третье число равно треугольному числу четвёртое число является тетраэдрическим[3]. m -е число равно биномиальному коэффициенту Сумма чисел восходящей диагонали, начинающейся с первого элемента (n -1)-й строки, есть n -е число Фибоначчи:[3]
Если вычесть из центрального числа в строке с чётным номером соседнее число из той же строки, то получится число Каталана.[3] Сумма чисел n -й строки треугольника Паскаля равна Все числа в n -й строке, кроме единиц, делятся на число n, если и только если n является простым числом[4] (следствие теоремы Люка). Простые делители чисел треугольника Паскаля образуют детерминистские фракталы с вращательной симметрией 3-го порядка, которые в полной мере выявляются учётом показателей степеней простых делителей [6]. Если в строке с нечётным номером сложить все числа с порядковыми номерами вида 3 n, 3 n +1, 3 n +2, то первые две суммы будут равны, а третья на 1 меньше. Каждое число в треугольнике равно количеству способов добраться до него из вершины, перемещаясь либо вправо-вниз, либо влево-вниз. Полиномиальная формула. Формула (х1+х2+…+хk)n =
называется полиномиальной, где суммирование выполняется по всем решениям уравнения n1+n2+ …+ nk = n в целых неотрицательных числах, ni
Для доказательства выполним умножение
(х1+х2+…+хk)·(х1+х2+…+хk) … (х1+х2+…+хk) = (х1+х2+…+хk)n.
n
Чтобы привести подобные в полученном выражении, необходимо подсчитать количество одночленов вида
n
будет равно числу Рекуррентные соотношения. ! Свойства Производящая функция суммы (или разности) двух последовательностей равна сумме (или разности) соответствующих производящих функций. Произведение производящих функций
Примеры использования Пусть При фиксированном m производящей функцией последовательности
Поэтому число
Задача Фибоначчи Пусть в огороженном месте имеется пара кроликов (самка и самец) в первый день января. Эта пара кроликов производит новую пару кроликов в первый день февраля и затем в первый день каждого следующего месяца. Каждая новорожденная пара кроликов становится зрелой уже через месяц и затем через месяц дает жизнь новой паре кроликов. Возникает вопрос: сколько пар кроликов будет в огороженном месте через год, то есть через 12 месяцев с начала размножения?"
Производящая функция Последовательность числа разбиений
Размещение без повторений Размещения без повторений — комбинаторные соединения, составленные из n элементов по m. При этом два соединения считаются различными, если они либо отличаются друг от друга хотя бы одним элементом, либо состоят из одних и тех же элементов, но расположенных в разном порядке. формула для нахождения количества размещений без повторений:
формула для нахождения количества размещений с повторениями: Перестановки. В комбинаторике перестано́вка — это упорядоченный набор чисел Свойства: Число всех перестановок порядка
Композиция определяет операцию произведения на перестановках одного порядка: Любая группа является подгруппой группы перестановок множества элементов этой группы (теорема Кэли). При этом каждый элемент Сочетания. В комбинаторике сочетанием из Так, например, наборы (3-хэлементные сочетания, подмножества, В общем случае число, показывающее, сколькими способами можно выбрать Сочетания с повторениями. Сочетанием с повторениями называются наборы, в которых каждый элемент может участвовать несколько раз. Число сочетаний с повторениями из
При фиксированном
Двумерной производящей функцией чисел сочетаний с повторениями является:
Бином Ньютона. Бино́м Нью́то́на — формула для разложения на отдельные слагаемые целой неотрицательной степени суммы двух переменных, имеющая вид
где В таком виде эта формула была известна ещё индийским и исламским математикам; Ньютон вывел формулу бинома для более общего случая, когда показатель степени — произвольное рациональное число (возможно, отрицательное). В этом случае бином представляет собой бесконечный ряд Свойства бинома Ньютона Разложение бинома (a + b)n представляет собой многочлен, расположенный по убывающим степеням a (от n-й до нулевой) и по возрастающим степеням b (от нулевой до n-й); сумма показателей a и b в каждом члене разложения равна показателю степени бинома. Число членов разложения на единицу больше показателя степени бинома. Коэффициенты членов разложения («биноминальные коэффициенты») возрастают до середины разложения и затем убывают; коэффициенты каждой пары членов, равноотстоящих от начала и конца разложения, равны между собой. Если n четное, то имеется один средний наибольший коэффициент; если n нечетное, то имеется два средних наибольших коэффициента. При возведении в n-ю степень разности a - b все четные члены разложения имеют знак "минус": Треугольник Паскаля. Треугольник Паскаля — бесконечная таблица биномиальных коэффициентов, имеющая треугольную форму. В этом треугольнике на вершине и по бокам стоят единицы. Каждое число равно сумме двух расположенных над ним чисел. Строки треугольника симметричны относительно вертикальной оси. Назван в честь Блеза Паскаля. Свойства Числа треугольника симметричны(равны) относительно вертикальной оси. В строке с номером n: первое и последнее числа равны 1. второе и предпоследнее числа равны n. третье число равно треугольному числу четвёртое число является тетраэдрическим[3]. m -е число равно биномиальному коэффициенту Сумма чисел восходящей диагонали, начинающейся с первого элемента (n -1)-й строки, есть n -е число Фибоначчи:[3]
Если вычесть из центрального числа в строке с чётным номером соседнее число из той же строки, то получится число Каталана.[3] Сумма чисел n -й строки треугольника Паскаля равна Все числа в n -й строке, кроме единиц, делятся на число n, если и только если n является простым числом[4] (следствие теоремы Люка). Простые делители чисел треугольника Паскаля образуют детерминистские фракталы с вращательной симметрией 3-го порядка, которые в полной мере выявляются учётом показателей степеней простых делителей [6]. Если в строке с нечётным номером сложить все числа с порядковыми номерами вида 3 n, 3 n +1, 3 n +2, то первые две суммы будут равны, а третья на 1 меньше. Каждое число в треугольнике равно количеству способов добраться до него из вершины, перемещаясь либо вправо-вниз, либо влево-вниз. Перестановки с повторениями. Последовательность длины n, составленная из k разных символов, первый из которых повторяется n 1 раз, второй — n 2 раз, третий — n 3 раз,…, k -й — nk раз (где n 1+ n 2+ … + nk = n) называется перестановкой с повторениями из n элементов. Например, пусть дан набор из четырех букв aabc. Тогда все перестановки с повторениями из этих букв суть abac, baac, aabc, aacb, abca, baca, acba, acab, bcaa, cbaa, caba, caab. Число перестановок с повторениями длины n из k разных элементов, взятых соответственно по n 1, n 2, …, nk раз каждый обозначается P (n 1, n 2, …, nk) и равно n! / (n 1! n 2! … nk!). В рассмотренном выше примере, букв a в исходном наборе две, а букв b и с — по одной. Следовательно, количество всех перестановок с повторениями из 4 элементов и составом букв 2, 1, 1 равно P (2, 1, 1) = 4! / (2! 1! 1!) = 12, в чем мы и убедились. Полиномиальная формула. Формула (х1+х2+…+хk)n =
называется полиномиальной, где суммирование выполняется по всем решениям уравнения n1+n2+ …+ nk = n в целых неотрицательных числах, ni
Для доказательства выполним умножение
(х1+х2+…+хk)·(х1+х2+…+хk) … (х1+х2+…+хk) = (х1+х2+…+хk)n.
n
Чтобы привести подобные в полученном выражении, необходимо подсчитать количество одночленов вида
n
будет равно числу Рекуррентные соотношения. !
|
||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 927; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.141 (0.009 с.) |


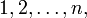 обычно трактуемый как биекция на множестве
обычно трактуемый как биекция на множестве  , которая числу i ставит соответствие i -й элемент из набора. Число n при этом называется порядком перестановки. Как синоним слову "перестановка" в этом смысле некоторые авторы используют слово расстановка.
, которая числу i ставит соответствие i -й элемент из набора. Число n при этом называется порядком перестановки. Как синоним слову "перестановка" в этом смысле некоторые авторы используют слово расстановка. равно числу размещений из n по n, то есть факториалу:[1][2][3][4]
равно числу размещений из n по n, то есть факториалу:[1][2][3][4]
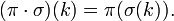 Относительно этой операции множество перестановок порядка n образует группу, которую называют симметрической и обычно обозначают
Относительно этой операции множество перестановок порядка n образует группу, которую называют симметрической и обычно обозначают  .
.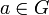 сопоставляется с перестановкой
сопоставляется с перестановкой  , задаваемой тождеством
, задаваемой тождеством  где g — произвольный элемент группы G, а
где g — произвольный элемент группы G, а  — групповая операция.
— групповая операция. называется набор
называется набор  ) {2, 1, 3} и {3, 2, 1} 6-тиэлементного множества {1, 2, 3, 4, 5, 6} (
) {2, 1, 3} и {3, 2, 1} 6-тиэлементного множества {1, 2, 3, 4, 5, 6} (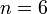 ) являются одинаковыми (однако, как размещения были бы разными) и состоят из одних и тех же элементов {1,2,3}.
) являются одинаковыми (однако, как размещения были бы разными) и состоят из одних и тех же элементов {1,2,3}.


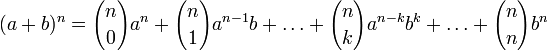 ,
, — биномиальные коэффициенты,
— биномиальные коэффициенты,  , что также равно сумме номеров предшествующих строк[3].
, что также равно сумме номеров предшествующих строк[3]. .
.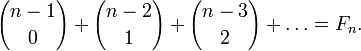
 [3].
[3]. (1)
(1) 0, I =1,2,…,k.
0, I =1,2,…,k.
 каждого разбиения n1+n2+ …+ nk = n. Для получения же одночлена
каждого разбиения n1+n2+ …+ nk = n. Для получения же одночлена  способами. Из оставшихся n – n1 не раскрытых скобок необходимо выбрать х2 в качестве множителя в n2 скобках. Это можно сделать
способами. Из оставшихся n – n1 не раскрытых скобок необходимо выбрать х2 в качестве множителя в n2 скобках. Это можно сделать  способами и т.д. Тогда количество одночленов
способами и т.д. Тогда количество одночленов  (х1+х2+…+хk)·(х1+х2+…+хk) … (х1+х2+…+хk)
(х1+х2+…+хk)·(х1+х2+…+хk) … (х1+х2+…+хk) =
=  упорядоченных разбиений.
упорядоченных разбиений. и
и  последовательностей
последовательностей  и
и  является производящей функцией свёртки
является производящей функцией свёртки  этих последовательностей:
этих последовательностей:
 — это количество композиций неотрицательного целого числа n длины m, то есть, представлений n в виде
— это количество композиций неотрицательного целого числа n длины m, то есть, представлений n в виде  , где
, где  — неотрицательныецелые числа. Число
— неотрицательныецелые числа. Число  (при этом каждый член
(при этом каждый член 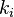 в композиции можно трактовать как количество элементов i в выборке).
в композиции можно трактовать как количество элементов i в выборке). является:
является:
 в разложении
в разложении  по степеням x. Для этого можно воспользоваться определением биномиальных коэффициентов или же непосредственно взять n раз производную в нуле:
по степеням x. Для этого можно воспользоваться определением биномиальных коэффициентов или же непосредственно взять n раз производную в нуле:
 имеет следующую производящую функцию:
имеет следующую производящую функцию:



