
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Классическое определение вероятности, свойства вероятности.
Классификация событий. Событие - опытом или испытанием наз. осуществление определенного комплекта условий или действий, при котором происходит соответствующее явление. Возможным результатом опыта наз. событие. Событие наз.достоверным если оно обязательно произойдет в данном опыте. Событие наз.невозможным если оно не может произойти в этом опыте. Событие наз.случайным если оно может произойти, а может и не произойти в этом опыте. Два события наз. Совместными в данном опыте, если появление одного из них не исключает появление другого в данном опыте. Два события наз. Несовместными если они не могут произойти вместе при одном и том же испытании.(попадание и промах при одном выстреле-несовместные события). Несколько событий наз несовместными если они попарно несовместимы. Два события наз. Противоположными, если появление одного из них равносильно непоявлению одного из них равносильно непоявлению из них.(как в учебнике: Противоположными наз. Два единственно возможных события, образующих полную группу. Если одно из двух противоположных событий обозначено через А, то другое принято обозначать как А с черточкой над буквой (не А). События наз. Равновозможными если есть основания считать что ни одно из них не является более возможным чем другое. Несколько событий образуют полную группу событий, если в результате испытания появится хотя бы одно из них. 1) Классическое определение вероятности, свойства вероятности. 3) Вероятностью события наз. Отношение числа элементарных исходов, благоприятствующих данному событию,числу всех равновозможных исходов опыта в которых может появиться это событие.
Свойства вероятности. 1)Вероятность достоверного события равна 1.D(U)=1 2)Вероятность невозможного события равна 0. P(V)=0 3)Вероятность случайного события выражается положительным числом меньше 1. 0<P(A)<1 4) Вероятность любого события В удовлетворяет неравенством 0≤P(B)≤1
Размещение.Сочетание. Перестановки. Размещением из n элементов по m наз. Любое упорядоченное подмножество из m элементов множества, состоящие из n различных элементов. Размещение отличается порядком входящих в них элементов и составом. Число размещений из n по m обозначается Перестановкой из n элементов наз. Любое упорядоченное множество, в которое входит по одному разу все n размещенных элементов множества, обозначается Сочетанием из n элементов по m наз. Любое подмножество из m элементов, которое принадлежит множеству, состоящему из n различных элементов. Обозначается число сочетаний из n разных элементов по m Размещение и сочетание различаются тем что в размещении учитывается порядок, входящих в него элементов, а в сочетании не учитывается.
Определение факториала. Факториал-Произведение всех натуральных чисел до n включительно. n!=1∙2∙3∙…∙n 0!=1
Относительная частота события. Сопоставляя определения вероятности и относительной частоты, заключаем: определение вероятности не требует, чтобы испытания производились в действительности, Определение же относительной частоты предполагает, что испытания ыли произведены фактически. Другими словами, вероятность вычисляют до опыта, а относительную частоту до опыта. Относительной частотой события или частотой наз. отношение числа опытов,в котором появилось это событие к числу всех произведенных опытов.
n-число всех произведенных опытов. Геометрическая вероятность. Классическое определение вероятности предполагает, что число элементарных исходов конечно. На практике встречаются опыты для которых множество таких исходов бесконечно. Для того, чтобы преодолеть недостаток классического определения вероятности, состоящей в том, что оно не применимо к испытаниям с бесконечным числом исходов водят геометрическую вероятность- это вероятность попадания точки в область. А-попадания брошенной точки в область g, тогда геометрическая вероятность этого события определяется формулой:
6) 7) 8) 9) 10) Формула Бернули. Производятся испытания в каждом из которых может появиться события А или событие не А, если вероятность события А в одном испытании не зависит от появления его в любом другом, то испытания называются независимыми относительно события А. Будем считать, что испытания происходят в одинаковых условиях, и вероятность появления события А в каждом испытании одна и та же. Обозначим эту вероятность через p, а вероятность не А через q. P+q=1. Вероятность того, что в серии из n независимых испытаний события А появится ровно e раз и не появится (n-k) раз обозначим через
Биномиальное распределение. Предположим, что в одинаковых условиях производится n независимых испытаний, в результате каждого из которых может появиться событие А с вероятностью р или противоположное событие
Закон распределения дискретной случайной величины, определяемый формулой Бернулли, называется биноминальным. Постоянные n и р, входящие в формулу, называются параметрами биноминального распределения (q = 1 - р). Название биноминальное распределение объясняется тем, что правую часть равенства можно рассматривать как общий член разложения бинома Ньютона
Первый член Биномиальный закон распределения дискретной случайной величины можно представить в виде следующей таблицы
Классификация событий. Событие - опытом или испытанием наз. осуществление определенного комплекта условий или действий, при котором происходит соответствующее явление. Возможным результатом опыта наз. событие. Событие наз.достоверным если оно обязательно произойдет в данном опыте. Событие наз.невозможным если оно не может произойти в этом опыте. Событие наз.случайным если оно может произойти, а может и не произойти в этом опыте. Два события наз. Совместными в данном опыте, если появление одного из них не исключает появление другого в данном опыте. Два события наз. Несовместными если они не могут произойти вместе при одном и том же испытании.(попадание и промах при одном выстреле-несовместные события). Несколько событий наз несовместными если они попарно несовместимы. Два события наз. Противоположными, если появление одного из них равносильно непоявлению одного из них равносильно непоявлению из них.(как в учебнике: Противоположными наз. Два единственно возможных события, образующих полную группу. Если одно из двух противоположных событий обозначено через А, то другое принято обозначать как А с черточкой над буквой (не А). События наз. Равновозможными если есть основания считать что ни одно из них не является более возможным чем другое. Несколько событий образуют полную группу событий, если в результате испытания появится хотя бы одно из них. 1) Классическое определение вероятности, свойства вероятности. 3) Вероятностью события наз. Отношение числа элементарных исходов, благоприятствующих данному событию,числу всех равновозможных исходов опыта в которых может появиться это событие.
Свойства вероятности. 1)Вероятность достоверного события равна 1.D(U)=1 2)Вероятность невозможного события равна 0. P(V)=0 3)Вероятность случайного события выражается положительным числом меньше 1. 0<P(A)<1 4) Вероятность любого события В удовлетворяет неравенством 0≤P(B)≤1
|
||||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 453; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.94.180 (0.01 с.) |
 P-вероятность А-событие m-число элементарных исходов, благоприятствующих событию А. n-число всех равновозможных элементарных исходов опыта, образующих полную группу событий.
P-вероятность А-событие m-число элементарных исходов, благоприятствующих событию А. n-число всех равновозможных элементарных исходов опыта, образующих полную группу событий. m≤n и вычисляется по формуле
m≤n и вычисляется по формуле 
 .Это один из случаев размещения при котором
.Это один из случаев размещения при котором 

 W(A) частота
W(A) частота 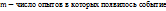
 для плоскости
для плоскости
 -Формула Бернули
-Формула Бернули с вероятностью q (q = 1 - р). В каждой серии из n испытаний событие А может либо не появиться, либо появиться 1 раз, 2 раза,..., n раз. Введем в рассмотрение дискретную случайную величину Х - "число появлений события А при n испытаниях". Найдем закон распределения этой случайной величины. Величина Х может принимать следующие значения: х0 = 0, х1 = 1, х2 = 2,..., хn = n. Вероятность pk того, что случайная величина Х принимает значение xk, вычисляется по формуле Бернулли
с вероятностью q (q = 1 - р). В каждой серии из n испытаний событие А может либо не появиться, либо появиться 1 раз, 2 раза,..., n раз. Введем в рассмотрение дискретную случайную величину Х - "число появлений события А при n испытаниях". Найдем закон распределения этой случайной величины. Величина Х может принимать следующие значения: х0 = 0, х1 = 1, х2 = 2,..., хn = n. Вероятность pk того, что случайная величина Х принимает значение xk, вычисляется по формуле Бернулли где
где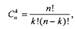 или
или 

 Поскольку р + q = 1, то
Поскольку р + q = 1, то т.е
т.е 
 в правой части разложения означает вероятность того, что в n испытаниях событие А не появится ни разу, второй член
в правой части разложения означает вероятность того, что в n испытаниях событие А не появится ни разу, второй член  - вероятность того, что событие А появится один раз, третий член
- вероятность того, что событие А появится один раз, третий член  - вероятность того, что событие А появится два раза, наконец, последний член
- вероятность того, что событие А появится два раза, наконец, последний член  - вероятность того, что событие А появится n раз.
- вероятность того, что событие А появится n раз.



