Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Простая колебательная система. Механическое сопротивление и его компоненты. Частотные характеристики.Содержание книги
Поиск на нашем сайте
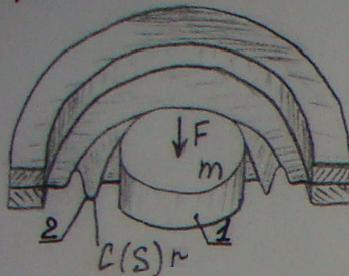
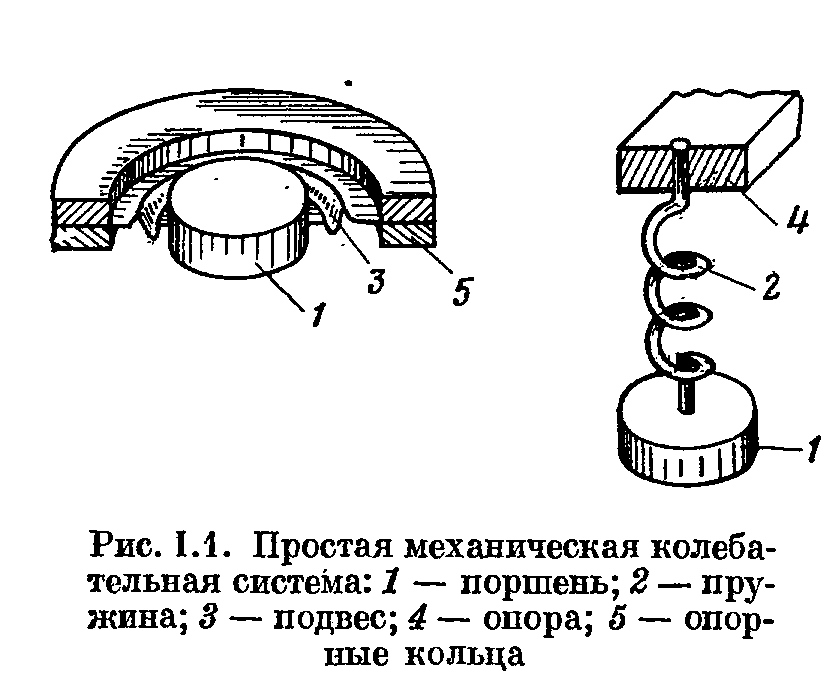
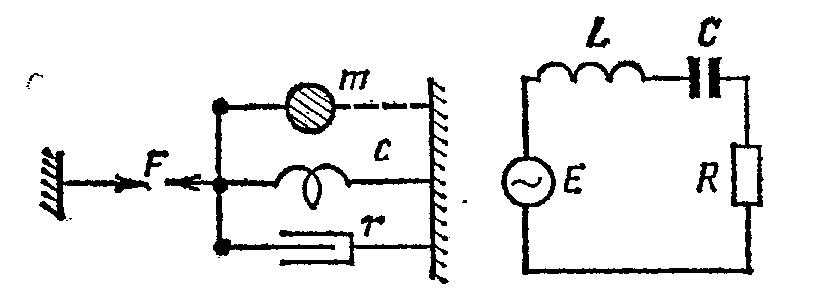
Простая колебательная система. Механическое сопротивление и его компоненты. Частотные характеристики. С 429 Простая колебательная система является составной частью почти любого ЭАА. Она состоит из жесткого поршня 1, прикрепленного к опоре подвесом 3 в виде гофрированного воротника, зажатого по внешнему периметру опорными кольцами 5, или с помощью спиральной пружины 2, второй конец которой заделан в опору 4.
Жесткий диск массой m с – коэффициент гибкости пружины
F=s*ξ – смещение конца пружины Закон Гука: s=F/ ξ Сила в каждый момент времени встречает противодействие, обусловленное инерцией поршня, упругостью пружины подвеса и трением. Реакция, вызываемая инерцией, пропорциональна массе поршня m и приобретенному им к моменту времени t ускорению:
Смещения, с которыми приходится иметь дело в акустике, весьма незначительны по величине, поэтому деформация пружины подвеса, как правило, не переходит за пределы закона Гука и ее реакцию можно считать пропорциональной относительному смещению концов:
Коэффициент гибкости численно равен смещению ее конца под воздействием единичной силы. Трение может быть: сухим (кулоновским), вязким (жидкостным- трение о воздух(воду)), внутренним(внутреннее трение пружины). F3 = Силы 1,2,3 – внутренние силы массы, гибкости и трения (силы противодействия этих элементов внешней силе) На основе принципа Даламбера можем составить теперь уравнение равновесия системы:
При
Зная это, построим частотные зависимости амплитуд смещения, скорости и ускорения.
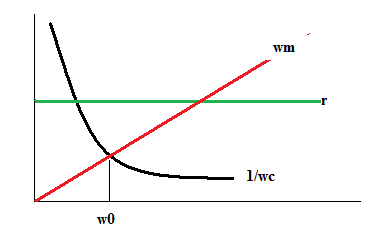
Реактивные составляющие работают друг против друга До резонанса – преобладает упругое сопротивление, После – инерционное На резонансе – активное На резонансной частоте реактивные сопротивления равны, при этом каждое из них равно характеристическому сопротивлению
С 436 Анализ сложных механических систем осуществляется методом электромеханических аналогий.
Электрические колебания в контуре L-индуктивность контура R – активное сопротивление С – емкость e – мгновенное значение приложенной к контуру ЭДС q- мгновенное значение заряда(с точкой – тока)
В основу аналогии положено соответствие между колебательной скоростью и током. В механической системе сила вызывает колебания со скоростью, в электрической – ЭДС(или напряжение) вызывает ток. для простейших систем составление эквивалентных схем – несложно. Для сложных механических систем рассмотрим один из методов составления эквивалентных схем, предложенный Беловым: 1.замена каждого подвижного узла(жесткое соединение полюсов нескольких элементов, движущихся совместно) механической модели последовательным электрическим контуром, составленным из аналогов тех элементов, полюса которых образуют один узел 2.совмещение одинаковых элементов, входящих в разные контуры.
Анализ механико-акустической системы: 1.идентификация элементов, структуры, масс -сначала массы, второй полюс всегда на опоре -затем пружины -все трения 2.составление динамической модели, которое начинается с обозначения опор и цепочечного размещения между ними всех масс, затем пружины, сопротивления. Соединения отражает узловые структуры 3.сопостовление размещения полюсов элементов в конструкции Звуковое поле. Параметры звукового поля. Свойства звуковых полей, создаваемых источниками различных волн: сферических, плоских, промежуточными формами фронта. Характеристика направленности источника звука. С 6-7,21,24 Звуковой волной называется процесс распространения деформаций сжатия или разрежения в сплошной среде, происходящий с конечной скоростью, называемой скоростью звука. Звуковая волна может возникать и распространяться только в такой среде, которая обладает определенной упругостью (сжимаемостью) и инерционностью (плотностью). Область среды, в которой возбуждены звуковые волны – звуковое поле. Звуковая волна является продольной волной, то есть частицы среды при распространении такой волны совершают колебания вдоль направления распространения. Фронтом волны называют поверхность, проходящую через частицы среды, совершающие в результате распространения волны колебания с одной и той же фазой. Обычно рассматривают три типа звуковых волн: плоские – фронт в виде плоскости (поршень в трубе); шаровые (ГГ) – с фронтом в виде сферы и цилиндрические – фронт в виде боковой поверхности цилиндра(проезжающий поезд) Математически звуковая волна описывается волновым уравнением: В декартовых координатах
Свойства плоской волны: 1.звуковое давление и колебательная скорость совпадают по фазе, это говорит о чисто активном характере звуковой энергии, переносимой плоской волной. 2.звуковое давление и колебательная скорость не зависят от расстояния(для идеальной среды) 3.волновое сопротивление плоской волны - Свойства шаровой волны: Фронт волны 1.амплитуда звукового давления в шаровой волне изменяется обратно пропорционально расстоянию 2. колебательная скорость в поле шаровой волны имеет 2 составляющие – одна из них совпадает по фазе с давлением и называется активной, вторая отстает на 90 градусов – реактивная.
Характеристика направленности источника звука – диаграмма в полярных координатах, показывающая распределение звукового давления в зависимости от угла склонения θ (угол между осью излучения и направлением на данный приемник). R(θ) = P(θ)/P(0°) R(θ) = 0.5(1+cos θ) «кардиоида» R(θ) = cos θ «восьмерка»
Разновидности характеристик направленности: 1.слабонаправленные 2.ненаправленные 3.остронаправленные (угол направленного действия меньше 45).
Акустическая мощность источника звука, интенсивность звука (определение понятий). Взаимосвязь акустической мощности источника с осевой интенсивностью на заданном расстоянии. Понятие коэффициента осевой концентрации. ТОА пункт 3.4.2 Акустич. мощност ь = колебательная скорость в квадрате умножить на сопротивление излучения Формулы и графики оттуда Анализ показывает, что в НЧ излучаемая мощность круто спадает с уменьшением частоты ( Интенсивность звука – средний поток звуковой энергии, проносимой звуковой волной в одну секунду через единичную площадку, нормальную к направлению распространения звука. Измеряется в Вт/м2.
Для шаровой волны -
Для ненаправленного I= WАК/4Пr2 Для направленного I= (WАК/4Пr2)*Ω КОК – отношение акустических мощностей ненаправленного и направленного источников, создающих на одном и том же расстоянии на оси одинаковую интенсивность. Или КОК – отношение квадрата осевой чувствительности в условиях свободного поля к его значению, усредненному по всем направлениям на одной и той же частоте.
С41 Ощущения сенсорных органов пропорционально не линейной величине раздражения, а его логарифму.
N=lgn, так как Поскольку звуки столь сильно различаются по интенсивности, удобнее рассматривать ее как логарифмическую величину и измерять в децибелах. Логарифмическая величина интенсивности представляет собой логарифм отношения рассматриваемого значения величины к ее значению, принимаемому за исходное. Уровень интенсивности J по отношению к некоторой условно выбранной интенсивности J0 равен Уровень интенсивности звука = 10 lg (J/J0) дБ Таким образом, один звук, превышающий другой по уровню интенсивности на 20 дБ, превышает его в 100 раз по интенсивности. В практике акустических измерений принято выражать интенсивность звука через соответствующую амплитуду избыточного давления Р1. Когда давление измеряется в децибелах относительно некоторого условно выбранного давления Р0, получают так называемый уровень звукового давления. Уровень звукового давления = 20 lg (P1/P0) дБ Условное давление Р0 = 2*10—5 Па соответствует стандартному порогу слышимости для звука с частотой 1 кГц. Складывать дБ нельзя, надо переводить в интенсивности! Децибе́л — логарифмическая единица уровней, затуханий и усилений.
6. громкость звука и ее физические корреляты. Кривые равной громкости и уровень громкости. Методика определения УГ простых звуков и сложных звуков по методу Стивенса. Под уровнем громкости L данного звука понимают уровень интенсивности эталонного звука с частотой 1000 Гц, имеющего равную с данным звуком громкость. Уровень громкости измеряется в фонах. Число фонов, выражающих уровень громкости какого-либо звука, совпадает с числом дБ, выражающих уровень интенсивности равногромкого эталонного звука. Для определения уровня громкости синусоидальных звуков пользуются семейством кривых равной громкости.
Каждая кривая этого семейства получена путем субъективного уравнивания громкости синусоидального звука какой-либо произвольной частоты с громкостью эталонного звука 1000 Гц, уровень интенсивности которого в пределах одной кривой остается неизменным. При снятии кривой испытуемый регулирует звуковое давление звука произвольной частоты, делая его то тише, то громче эталонного, и добивается такой громкости, которая не отличалась бы от громкости эталонного звука. После этого производится измерение уровня звукового давления регулируемого звука, и опыт повторяется для другой частоты. Пройдя таким образом весь звуковой диапазон, получают кривую равной громкости или изофон, вид которого в значительной мере зависит от индивидуальных особенностей испытуемого слуха. Поэтому описанная процедура производится для групп слушателей с последующей статистической обработкой результатов. В пределах каждой кривой уровень громкости звуков имеет одну и ту же величину, численно равную уровню интенсивности на частоте 1000 Гц. Описанная процедура измерения кривых равной громкости – способ уравнивания. Пользуясь кривыми, можно определить уровень громкости любого синусоидального звука. Если известны уровень его интенсивности и частота. Например частота – 100 Гц, уровень – 50 дБ, найдем на их пересечении изофон, переместившись по которому к частоте 1000 Гц, увидим, что равногромкий с данным звуком эталонный звук должен иметь уровень интенсивности 40 дБ, это и есть искомый уровень громкости 40 фон. При высоких уровнях КРГ более равномерны, ЧХ восприятия при больших уровнях более равномерна. Уровень воспроизведения должен быть равен естественному уровню звука, иначе происходят тембральные искажения! Под громкостью звука понимают субъективную количественную меру его ощущения, для которого главным параметром раздражения(физическим коррелятом) является звуковое давление. Громкость звука зависит и от других параметров, таких, как спектр звука, длительность его воздействия и условия восприятия, но эта зависимость незначительна. Музыкальная шкала:fff, ff,f,mf,mp,p,pp,ppp Гипотеза Флетчера: громкость пропорциональна количеству нервных импульсов, поступающих в соответствующие мозговын центры от базилярной мембраны внутреннего уха. единица громкости – громкость звука 1000 Гц и уровнем интенсивности 40 дБ - сон
Метод Стивенса: 1. Получение объективной информации о сложном звуке, то есть измерение энергетического спектра сложного звука(диаграмма, показывающая столбиками, примыкающими друг к другу, распределение энергии сложного звука по частотным интервалам) 2. Для каждой полосы по уровню интенсивности и кривым Стивенса определяем индекс громкости 3. Из всех громкостей берем самую большую. Все остальные складываем и придавливаем по величине с помощью коэффициента маскировки, затем складываем с основным уровнем громкости: Недостаток – результат отстает на 0,5 – 1 с По Флетчеру: надо знать fk и уровень интенсивности, по этим данным – уровень громкости, затем – громкость, общая громкость складывается, по ней уровень громкости. Факторы, влияющие на звукопоглощающую способность материалов и конструкций. отражение и поглощение звуковой энергии на границе раздела двух сред. зависимость коэффициента звукопоглощения от акустического сопротивления материала. когда звуковая волна встречает препятствие в виде стен помещения, имеющих размеры, превосходящие длину падающей волны, часть энергии волны, преломляясь на границе препятствия, поглощается и передается через препятствие, а остальная энергия отражается обратно.
интенсивность падающей волны можно представить как
либо
при разработке ЗПК необходимо обеспечить 2 условия: 1.согласования значений входного акустического сопротивления ЗПК с волновым сопротивлением среды 2.поглощение энергии звука, прошедшей в материал ЗПК первое из условий определяет требование к физ.свойствам ЗПМ – значение волнового сопротивления ЗПМ должно быть соизмеримо с волновым сопротивлением воздушной среды 430Н*с/м3
Простая колебательная система. Механическое сопротивление и его компоненты. Частотные характеристики. С 429 Простая колебательная система является составной частью почти любого ЭАА. Она состоит из жесткого поршня 1, прикрепленного к опоре подвесом 3 в виде гофрированного воротника, зажатого по внешнему периметру опорными кольцами 5, или с помощью спиральной пружины 2, второй конец которой заделан в опору 4.
Жесткий диск массой m с – коэффициент гибкости пружины
F=s*ξ – смещение конца пружины Закон Гука: s=F/ ξ Сила в каждый момент времени встречает противодействие, обусловленное инерцией поршня, упругостью пружины подвеса и трением. Реакция, вызываемая инерцией, пропорциональна массе поршня m и приобретенному им к моменту времени t ускорению:
Смещения, с которыми приходится иметь дело в акустике, весьма незначительны по величине, поэтому деформация пружины подвеса, как правило, не переходит за пределы закона Гука и ее реакцию можно считать пропорциональной относительному смещению концов:
Коэффициент гибкости численно равен смещению ее конца под воздействием единичной силы. Трение может быть: сухим (кулоновским), вязким (жидкостным- трение о воздух(воду)), внутренним(внутреннее трение пружины). F3 = Силы 1,2,3 – внутренние силы массы, гибкости и трения (силы противодействия этих элементов внешней силе) На основе принципа Даламбера можем составить теперь уравнение равновесия системы:
При
Зная это, построим частотные зависимости амплитуд смещения, скорости и ускорения.
Реактивные составляющие работают друг против друга До резонанса – преобладает упругое сопротивление, После – инерционное На резонансе – активное На резонансной частоте реактивные сопротивления равны, при этом каждое из них равно характеристическому сопротивлению
С 436 Анализ сложных механических систем осуществляется методом электромеханических аналогий.
Электрические колебания в контуре L-индуктивность контура R – активное сопротивление С – емкость e – мгновенное значение приложенной к контуру ЭДС q- мгновенное значение заряда(с точкой – тока)
В основу аналогии положено соответствие между колебательной скоростью и током. В механической системе сила вызывает колебания со скоростью, в электрической – ЭДС(или напряжение) вызывает ток. для простейших систем составление эквивалентных схем – несложно. Для сложных механических систем рассмотрим один из методов составления эквивалентных схем, предложенный Беловым: 1.замена каждого подвижного узла(жесткое соединение полюсов нескольких элементов, движущихся совместно) механической модели последовательным электрическим контуром, составленным из аналогов тех элементов, полюса которых образуют один узел 2.совмещение одинаковых элементов, входящих в разные контуры.
Анализ механико-акустической системы: 1.идентификация элементов, структуры, масс -сначала массы, второй полюс всегда на опоре -затем пружины -все трения 2.составление динамической модели, которое начинается с обозначения опор и цепочечного размещения между ними всех масс, затем пружины, сопротивления. Соединения отражает узловые структуры 3.сопостовление размещения полюсов элементов в конструкции Звуковое поле. Параметры звукового поля. Свойства звуковых полей, создаваемых источниками различных волн: сферических, плоских, промежуточными формами фронта. Характеристика направленности источника звука. С 6-7,21,24 Звуковой волной называется процесс распространения деформаций сжатия или разрежения в сплошной среде, происходящий с конечной скоростью, называемой скоростью звука. Звуковая волна может возникать и распространяться только в такой среде, которая обладает определенной упругостью (сжимаемостью) и инерционностью (плотностью). Область среды, в которой возбуждены звуковые волны – звуковое поле. Звуковая волна является продольной волной, то есть частицы среды при распространении такой волны совершают колебания вдоль направления распространения. Фронтом волны называют поверхность, проходящую через частицы среды, совершающие в результате распространения волны колебания с одной и той же фазой. Обычно рассматривают три типа звуковых волн: плоские – фронт в виде плоскости (поршень в трубе); шаровые (ГГ) – с фронтом в виде сферы и цилиндрические – фронт в виде боковой поверхности цилиндра(проезжающий поезд) Математически звуковая волна описывается волновым уравнением: В декартовых координатах
Свойства плоской волны: 1.звуковое давление и колебательная скорость совпадают по фазе, это говорит о чисто активном характере звуковой энергии, переносимой плоской волной. 2.звуковое давление и колебательная скорость не зависят от расстояния(для идеальной среды) 3.волновое сопротивление плоской волны - Свойства шаровой волны: Фронт волны 1.амплитуда звукового давления в шаровой волне изменяется обратно пропорционально расстоянию 2. колебательная скорость в поле шаровой волны имеет 2 составляющие – одна из них совпадает по фазе с давлением и называется активной, вторая отстает на 90 градусов – реактивная.
Характеристика направленности источника звука – диаграмма в полярных координатах, показывающая распределение звукового давления в зависимости от угла склонения θ (угол между осью излучения и направлением на данный приемник). R(θ) = P(θ)/P(0°) R(θ) = 0.5(1+cos θ) «кардиоида» R(θ) = cos θ «восьмерка»
Разновидности характеристик направленности: 1.слабонаправленные 2.ненаправленные 3.остронаправленные (угол направленного действия меньше 45).
Акустическая мощность источника звука, интенсивность звука (определение понятий). Взаимосвязь акустической мощности источника с осевой интенсивностью на заданном расстоянии. Понятие коэффициента осевой концентрации. ТОА пункт 3.4.2 Акустич. мощност ь = колебательная скорость в квадрате умножить на сопротивление излучения Формулы и графики оттуда Анализ показывает, что в НЧ излучаемая мощность круто спадает с уменьшением частоты ( Интенсивность звука – средний поток звуковой энергии, проносимой звуковой волной в одну секунду через единичную площадку, нормальную к направлению распространения звука. Измеряется в Вт/м2.
Для шаровой волны -
Для ненаправленного I= WАК/4Пr2 Для направленного I= (WАК/4Пr2)*Ω КОК – отношение акустических мощностей ненаправленного и направленного источников, создающих на одном и том же расстоянии на оси одинаковую интенсивность. Или КОК – отношение квадрата осевой чувствительности в условиях свободного поля к его значению, усредненному по всем направлениям на одной и той же частоте.
|
||||
|
Последнее изменение этой страницы: 2016-09-17; просмотров: 1007; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.138.114.198 (0.013 с.) |

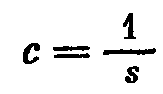 (s-коэффициент упругости пружины, численно равный силе, под действием которой получается единичное смещение ее конца)
(s-коэффициент упругости пружины, численно равный силе, под действием которой получается единичное смещение ее конца)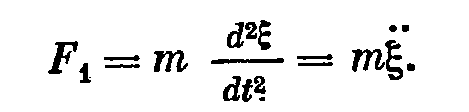
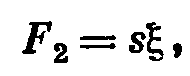 или
или 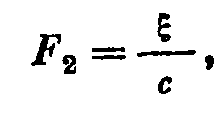

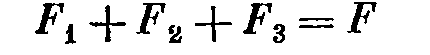 Или
Или 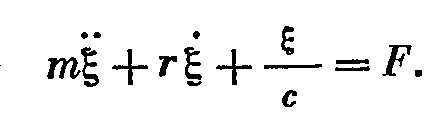
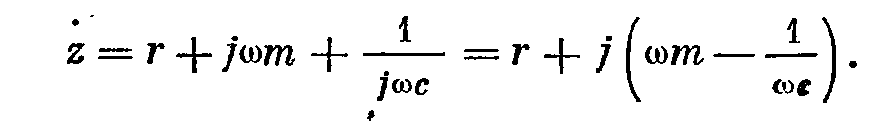 - отношение силы к скорости называется полным механическим сопротивление колебательной системы и состоит из трех парциальных сопротивлений – активного r, инерционного jwm и упругого 1/jwc. Два последних – реактивное сопротивление.
- отношение силы к скорости называется полным механическим сопротивление колебательной системы и состоит из трех парциальных сопротивлений – активного r, инерционного jwm и упругого 1/jwc. Два последних – реактивное сопротивление.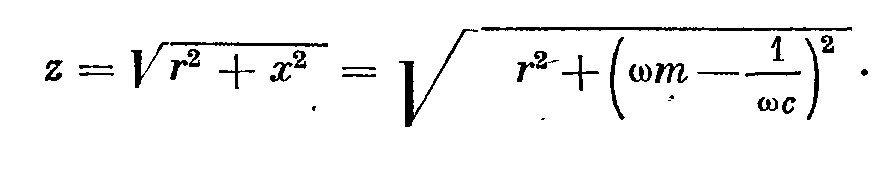 - модуль, используется при расчете.
- модуль, используется при расчете.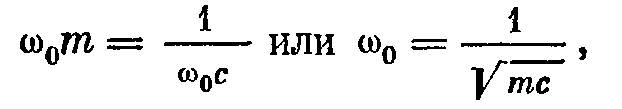 реактивная часть полного механического сопротивления исчезает, модуль принимает минимальное значение, равное активному сопротивлению. А колебательная скорость будет максимальной – резонанс, а w0 – резонансная частота.
реактивная часть полного механического сопротивления исчезает, модуль принимает минимальное значение, равное активному сопротивлению. А колебательная скорость будет максимальной – резонанс, а w0 – резонансная частота.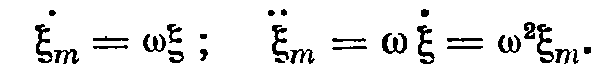
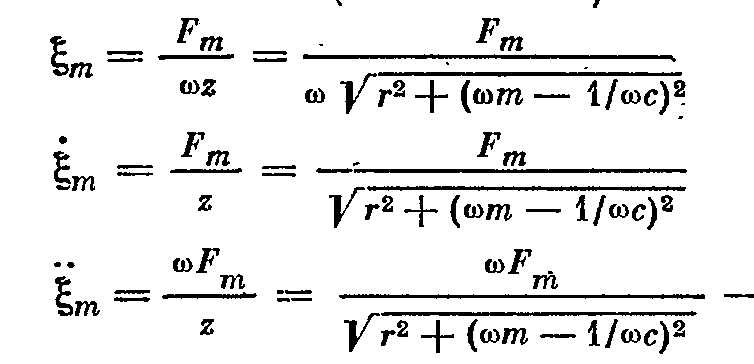
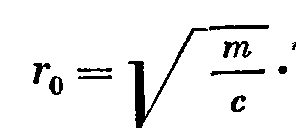
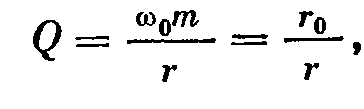 -добротность
-добротность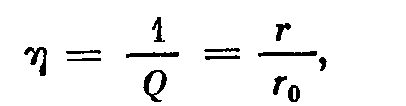 -коэффициент потерь
-коэффициент потерь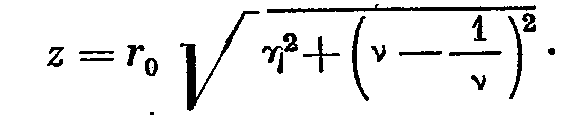
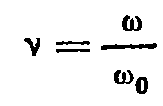
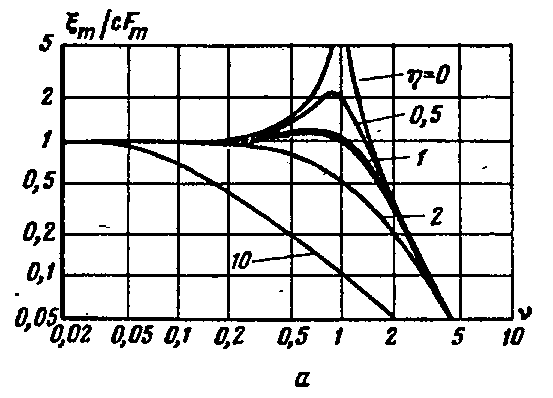
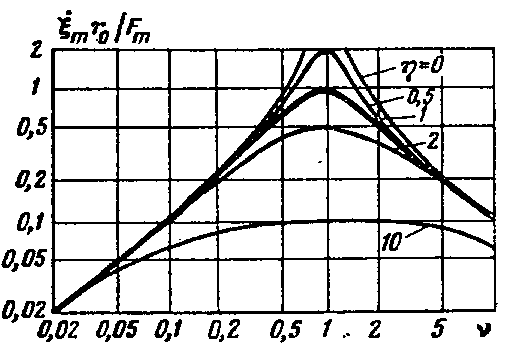
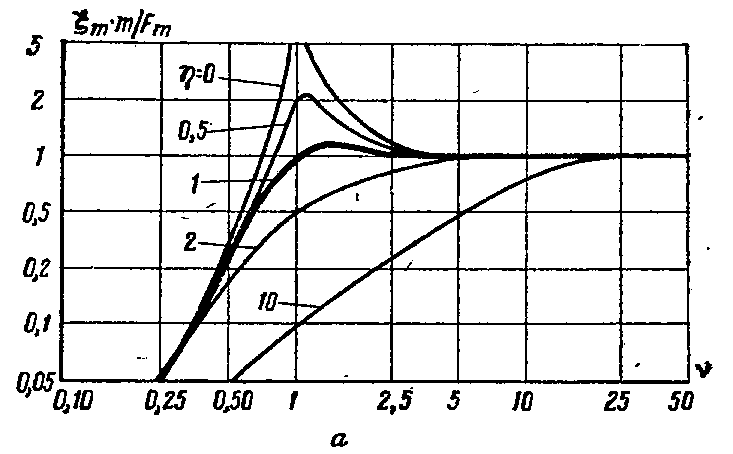
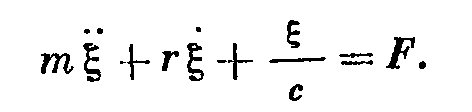
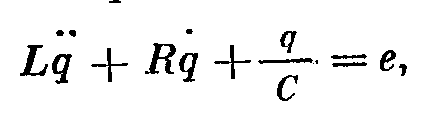

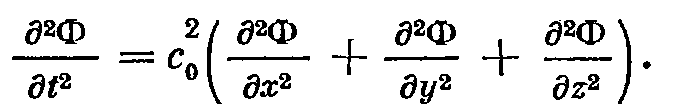
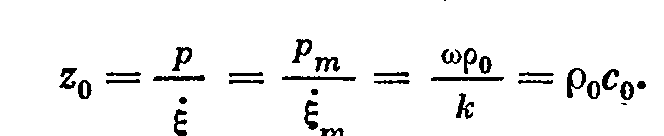
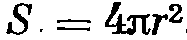
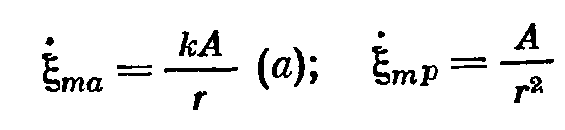
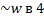 ), в третьей зоне – ОВЧ: сопротивление излучения перестает расти, но система продолжает управляться массой. Колебательная скорость уменьшается, отсюда следует, что мощность падает обратно пропорционально частоте в квадрате. В средней части – оптимизация характеристики, она становится равномерной по той причине, что уменьшение колебательной скорости (ее квадрата) компенсируется квадратичным возрастанием сопротивления излучения.
), в третьей зоне – ОВЧ: сопротивление излучения перестает расти, но система продолжает управляться массой. Колебательная скорость уменьшается, отсюда следует, что мощность падает обратно пропорционально частоте в квадрате. В средней части – оптимизация характеристики, она становится равномерной по той причине, что уменьшение колебательной скорости (ее квадрата) компенсируется квадратичным возрастанием сопротивления излучения.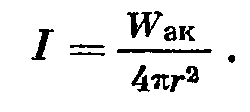
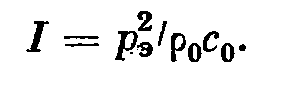 - для любого фронта.
- для любого фронта.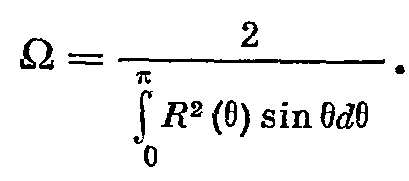





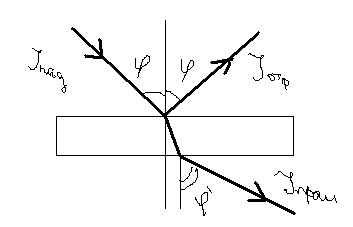 относительные величины отраженных, поглощенных и прошедших энергий звуковой волны зависят главным образом от природы материала препятствия. геометрические размеры препятствия определяют частотную зависимость указанных величин.
относительные величины отраженных, поглощенных и прошедших энергий звуковой волны зависят главным образом от природы материала препятствия. геометрические размеры препятствия определяют частотную зависимость указанных величин.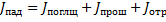
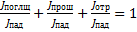
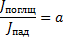
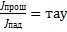
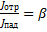

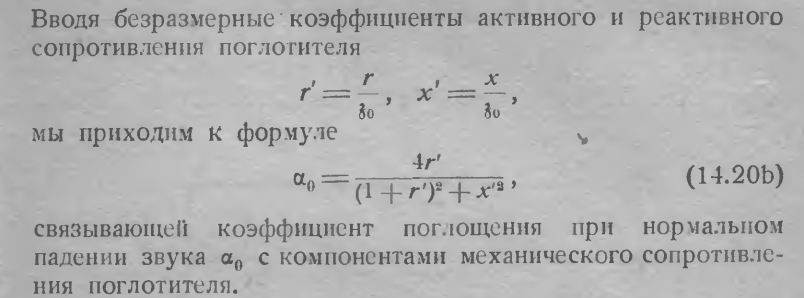 звукопоглощающие материалы должны иметь минимальную плотность, максимальный объем воздухонасыщения, максимальную площадь поверхности воздушных включений(пор, пространства между волокнами).
звукопоглощающие материалы должны иметь минимальную плотность, максимальный объем воздухонасыщения, максимальную площадь поверхности воздушных включений(пор, пространства между волокнами).