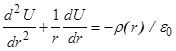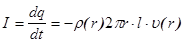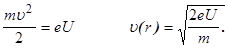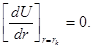Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Ненасыщенного вакуумного диода.Содержание книги
Поиск на нашем сайте
Цель работы: Экспериментальное определение отношения заряда электрона к его массе по вольт-амперной характеристике ненасыщенного вакуумного диода. Введение
Вольт-амперной характеристикой (ВАХ) вакуумного диода называют зависимость анодного тока от напряжения между анодом и катодом диода. Различают три участка вольт-амперной характеристики. Первый участок соответствует малому изменению анодного тока и может находиться при отрицательном и положительном значениях анодного напряжения. Этот участок расположен на ВАХ от I=0 до ее прямолинейной части. Второй прямолинейный участок вольт-амперной характеристики показывает ее зависимость I=f(U) до насыщения анодного тока. Третий участок соответствует насыщению анодного тока. В настоящей работе в качестве рабочей используется область пространственного заряда ВАХ, который, образуясь вблизи катода, уменьшает анодный ток, так как электрическое поле пространственного заряда препятствует движению электронов к аноду и часть из них возвращает обратно на катод, т. е. анодный ток меньше тока эмиссии. Как показывает опыт, зависимость анодного тока от напряжения на диоде в области пространственного заряда подчиняется «закону трех вторых» Ленгмюра:
где b — коэффициент пропорциональности, зависящий от материала катода, его формы, а также от удельного заряда электрона. Следовательно, измерив зависимость анодного тока диода от напряжения на его аноде в области пространственного заряда, можно определить удельный заряд электрона. Получим выражение для коэффициента пропорциональности в «законе трех вторых». Для этого рассмотрим движение электронов в вакуумном диоде типа 2Ц2С, применяемом в данной работе. Электроды этой лампы представляют собой коаксиальные (соосные) цилиндры. Меньший электрод радиусом rk, являющийся катодом, вложен во второй электрод радиусом ra, являющийся анодом. Между анодом и катодом создается разность потенциалов U. Потенциал катода считаем равным нулю. Пренебрегая краевыми эффектами, связанными с конечной длиной катода, флуктуациями напряжения и пространственного заряда, будем считать электрическое поле между анодом и катодом цилиндрически симметричным и независящим от времени (стационарным). В плоскости, перпендикулярной оси цилиндрического анода, введем полярную систему координат с полюсом на оси цилиндра. Расстояние от полюса обозначим через r (см.рисунок). Распределение потенциалов в пространстве между анодом и катодом вакуумного диода описывается уравнением Пуассона, которое в системе СИ записывается так:
где U — потенциал, r(r) — объемная плотность электрического заряда. Выразим плотность заряда через ток диода I. Для этого вырежем двумя сечениями перпендикулярно оси z слой толщиной i. В этом случае ток, протекающий через этот слой, для выбранной системы координат равен:
где u(r) —скорость электронов на расстоянии r от катода. Пренебрегая скоростью вылета электронов из катода, выразим скорость электронов u(r) через пройденную ими разность потенциалов:
Тогда выражение для тока принимает следующий вид:
Учитывая выполненные преобразования, уравнение Пуассона можно записать так:
где l — длина катода; е и m соответственно заряд и масса электрона, e0 =8,85/10-12 Ф / м. Полученное дифференциальное уравнение может быть решено, если заданы граничные условия и, кроме того, потенциал анода удовлетворяет следующему условию:
Поскольку производная du/dr равна напряженности электрического поля, это условие означает, что вблизи катода пространственный заряд электронов полностью компенсирует поле анода. В этом случае, как показывает расчет, решение уравнения Пуассона, удовлетворяющее поставленным условиям, можно записать в виде:
где ra — радиус анода; b — коэффициент, зависящий от соотношения значений радиуса анода ra и радиуса катода rk. Для данного типа лампы, как показывает расчет, b2 =0,98 Как видно из полученного выражения, представляющего собой «закон трех вторых» для коаксиальных цилиндрических электродов, можно определить удельный заряд электрона.
|
||||
|
Последнее изменение этой страницы: 2016-09-13; просмотров: 380; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.119 (0.006 с.) |

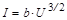 ,
,