
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Типове завдання модульної контрольної роботи № 4Содержание книги
Поиск на нашем сайте
1. Обчислити невизначені інтеграли: а). 2. Обчислити визначені інтеграли: а). 3. Обчислити невласні інтеграли або довести їх розбіжність:а). 4. Знайти обсяг продукції випущеної фірмою за 5 років, якщо виробнича функція Кобба-Дугласа має вид: 5. Розподіл прибуткового податку деякої країни здійснюється відповідно до функції 6. Розв’язати диференціальне рівняння з відокремленими змінними:
7. Розв’язати однорідне диференціальне рівняння: 8. Розв’язати лінійне диференціальне рівняння: 9. Знайти загальний розвязок рівняння: Контрольні запитання до змістовного модуля 4. 1. Яке означення первісної функції? 2. Які основні властивості первісної? 3. Що називається невизначеним інтегралом? 4. Якіосновні властивості невизначеного інтегралу? 5. Випишіть таблицю основних невизначених інтегралів. 6. Яка формула заміни змінної у невизначеному інтегралі? 7. В чому полягаж суть методу інтегрування частинами? 8. Які функції називаються дробово-раціональними? 9. Який раціональний дріб називається правильним, неправильним? 10. Який зв’язок існує між ними? 11. Як інтегруються елементарні дробово-раціональні функції? 12. Як правильний раціональний дріб розкладається на суму елементарних? 13. В чому суть методу невизначених коефіцієнтів? 14. Які Вам відомі методи інтегрування ірраціональних виразів? 15. Що таке універсальна тригонометрична підстановка? 16. Що таке інтегральна сума функції на відрізку? 17. Яке означення визначеного інтегралу функції на відрізку? 18. У чому полягає геометричний зміст визначеного інтегралу? 19. Які основні властивості визначеного інтегралу? 20. Які класи інтегровних функцій вам відомі? 21. Як записують формулу Ньютона-Лейбніца? 22. Як здійснюється заміна змінної у визначеному інтегралі? 23. Як записують формулу інтегрування частинами для визначеного інтеграла? 24. В чому відмінність між невласними інтегралами І та ІІ роду? 25. Як визначений інтеграл застосовують для обчислення площ фігур? 26. Як визначений інтеграл застосовують для обчислення довжин ліній? 27. Який вигляд має звичайне диференціальне рівняння n -го порядку?
28. Що називають розв’язком диференціального рівняння? 29. В чому різниця між загальним та частинним розв’язком диференціального рівняння? 30. Як записують задачу Коші? 31. Як розв’язують диференціальні рівняння першого порядку з відокремлюваними змінними? 32. Які диференціальні рівняння першого порядку називаються однорідними? 33. За допомогою якої заміни однорідні рівняння зводяться до рівнянь з відокремлюваними змінними? 34. Який вигляд мають лінійні диференціальні рівняння першого порядку? Якими методами вони розв’язуються? 35. Як розв’язуються лінійні диференційні рівняння другого порядку з сталими коефіцієнтами? Серед усіх видів навчальної роботи важливе місце належить самостійній підготовці студентів. Вона включає опрацювання теоретичного матеріалу лекцій, роботу з підручниками та навчальними посібниками, розв’язання задач математичного та економічного змісту. Завдання для самостійної роботи розраховані для впровадження кредитно-модульної системи “Математика для економіці” для студентів відділення «міжнародні економічні відносини» Інституту міжнародних відносин. Мета виконання самостійних робіт - набуття навичок самостійного вивчення наукової-методичної літератури з математичних дисциплін, розвитку математичного мислення; активізація самостійної роботи студентів та перевірка їх знань з відповідних розділів вищої математики. Для успішного складання заліку та іспиту за учбовим планом для студентів передбачено виконання самостійних робіт. Варіант для виконання завдань визначає викладач. Самостійна робота поділена на теми. Теми завдань повністю відповідають темам програми дисципліни “Математика в економіці”. Після опрацювання відповідного теоретичного матеріалу, студент самостійно виконує завдання і розв’язує задачі даного варіанту та відповідно оформлює виконану роботу і здає для перевірки. Результати кожної самостійної роботи, виконаної студентом, оцінюються відповідною кількостю балів. Після перевірки викладач оцінює кожну роботу та заносить відповідну кількість балів у відомість обліку успішності студентів в КМСОНП.
Правила оформлення самостійних робіт : Робота виконується на аркушах А4 і складається з наступних частин: 1. Титульна сторінка. 2. Короткі теоретичні відомості (короткий опис моделі, основні формули). 3. Формулювання задачі. 4. Результат обчислень та розв’язки задач. 5. Графік або діаграма (якщо є в роботі). 6. Висновки по роботі: · яка задача розв’язувалась, яким методом; · основні етапи розв’язання; · який результат отримано (чітка відповідь); · які висновки можна зробити на підставі розв’язку задачі. Короткі теоретичні відомості, розв’язки задач та висновки мають бути написані кожним студентом особисто від руки.
ЗАВДАННЯ ДЛЯ САМОСТІЙНОЇ РОБОТИ Завдання 1. Матриці. Визначники. Література [5] с.523-526, [6]с.663-666. Завдання 2. Методи розв’язування систем лінійних рівнянь. Література [5] с.527-530, [6]с.667-669. Завдання 3. Лінійні економічні задачі. Література [5] с.531-534, [6]с.670-673. Завдання 4. Вектори. Література [5] с.535-538, [6]с.674-676. Завдання 5. Елементи аналітичної геометрії. Література [5] с.539-542, [6]с.676-679. Завдання 6. Границя і неперервність функції. Література [5] с.543-546, [6]с.679-682. Завдання 7. Похідні та диференціали. Література [5] с.547-550, [6]с.683-686. Завдання 8. Застосування похідної до дослідження функцій. Література [5] с.551-554, [6]с.686-688. Завдання 9. Застосування похідної в економічних задачах Література [5] с.555-558, [6]с.689-692. Завдання 10. Функції багатьох змінних. Література [5] с.559-562, [6]с.6692-694. Завдання 11. Екстремуми функцій багатьох змінних. Література [5] с.563-566, [6]с.695-696. Завдання 12. Застосування функцій багатьох змінних в економічних задачах. Література [5] с.567-570, [6]с.697-699. Завдання 13. Невизначений інтеграл. Література [5] с.571-574, [6]с.700-702. Завдання 14. Визначені, невласні інтеграли. Застосування в економічних задачах. Література [5] с.575-578, [6]с.703-706. Завдання 15. Диференціальні рівняння. Література [6]с.707-708. ДЖЕРЕЛА ІНФОРМАЦІЇ а) основна література: 1. Валєєв К.Г., Джалладова І.А. Вища математика: Навчальний посібник: У 2-х ч. – Ч.1.- К.: КНЕУ, 2001. 2. Валєєв К.Г., Джалладова І.А. Вища математика: Навчальний посібник: У 2-х ч. – Ч.1.-К.: КНЕУ, 2002. 3. Вища математика: Основні означення, приклади і задачі. За ред. Кулініча Г.Л. К.: Либідь, 1992. 4. Вища математика: Підручник: У 2 кн. – 2-ге вид., - За ред. Кулініча Г.Л. К.: Либідь, 2003. 5. Грисенко М.В. Математика для економістів: Підручник.- К.: ВПЦ «Київський університет», 2008.- 599с. 6. Грисенко М.В. Математика для економістів. Методи і моделі, приклади і задачі: Навч. посібник.- К.: Либідь, 2007.- 720с. 7. Красс М.С., Чупрынов Б.П. Основы математики и ее приложения в экономическом образовании. М.: ДЕЛО, 2000. 8. Кремер Н. Высшая математика для экономистов. М.: ЮНИТИ, 1998. б) додаткова література: 9. Ашманов С.А. Математические модели и методы в экономике. М., 1980. 10. Anthony M., Biggs N. Mathematics for economics and finance. Methods and modelling. Cambridge University Press. 11. Бугір М.К. Математика для економістів. Тернопіль, 1998.
12. Барковський А.В., Барковська Н.В. Математика для економістів: Вища математика. К.: НАУ, 1997. 13. Замков О.О., Толстопятенко А.В., Черемных Ю.Н. Математические методы анализа экономики. М.: ДИС, 1997. 14. Керекеша П.В. Лекції і вправи з вищої математики.-О. "Астроприт". 2003 15. Малыхин В.И. Математика в экономике. М.:ИНФРА-М, 1999. 16. Міхайленко В.М., Федоренко Н.Д. Математичний аналіз для економістів. К. Європейський університет. 2002. 17. Пономаренко О.І., Перестюк М.О., Бурим В.М. Основи математичної економіки. – К.:ІНФОРМТЕХНІКА, 1995. 18. Солодовников А.С., Бабайцев В.А.,Браилов А.В., Шандра И.Г. Математика в экономике. М.: Финансы и статистика, 1999.
|
||||||||
|
Последнее изменение этой страницы: 2016-09-13; просмотров: 207; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.217.218.25 (0.009 с.) |

 б).
б). 
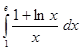 б).
б). 
 б).
б).  .
. .
. (крива Лоренца), де x – частина населення, що сплачує податки, а y – відповідна частина загального податку населення. Обчислити коефіцієнт Джині.
(крива Лоренца), де x – частина населення, що сплачує податки, а y – відповідна частина загального податку населення. Обчислити коефіцієнт Джині. .
. .
. .
. .
.


