
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Полная механическая энергия замкнутой консервативной системы не изменяется при любых перемещениях тел. Это утверждение называется законом сохранения механической энергии системы.Содержание книги
Поиск на нашем сайте
Заметим, что в процессе движения тел системы один вид энергии может переходить в другой.
Причины изменения механической энергии системы. Полной механической энергией системы тел называется сумма кинетической и потенциальной энергий: E = Eк + Eп. Какие причины могут изменить полную механическую энергию? Полная механическая энергия может изменяться в результате следующих причин:
9-10.Моментом инерции механической системы относительно неподвижной оси («осевой момент инерции») называется величина Ja, равная сумме произведений масс всех n материальных точек системы на квадраты их расстояний до оси:
где:
Осевой момент инерции тела Ja является мерой инертности тела во вращательном движении вокруг оси подобно тому, как масса тела является мерой его инертности в поступательном движении.
где:
Если тело однородно, то есть его плотность всюду одинакова, то
11.Теоре́ма Гю́йгенса — Ште́йнера, или просто теорема Штейнера (названа по имени швейцарского математика Якоба Штейнера и голландского математика, физика и астронома Христиана Гюйгенса): момент инерции тела J относительно произвольной оси равен сумме момента инерции этого тела JC относительно параллельной ей оси, проходящей через центр масс тела, и произведения массы тела m на квадрат расстояния d между осями:
где JC — известный момент инерции относительно оси, проходящей через центр масс тела, J — искомый момент инерции относительно параллельной оси, m — масса тела, d — расстояние между указанными осями. Вывод Момент инерции, по определению:
Радиус-вектор
где
Вынося за сумму
Поскольку старая ось проходит через центр масс, то суммарный импульс тела будет равен нулю:
Тогда:
Откуда и следует искомая формула:
где JC — известный момент инерции относительно оси, проходящей через центр масс тела. Момент силы, действующей на материальную точку. Пусть частица A движется произвольным образом относительно точки О под действием силы F (см. рис. 6.2). Моментом силы частицы относительно закрепленной точки называется величина, равная векторному произведению: M = [ r · F ], (6.3)
кинетическая энергия твердого тела при вращательном движении. Кинетическая энергия твердого тела складывается из кинетических энергий его частей Ei. Рассчитаем значение Ei для элементов твердого тела. Ei = mi·vi2/2 = mi·w2·ri2/2. Кинетическая энергия твердого тела будет равна: Eк = w2/2·Smi·ri2 = I·w2/2. (8.13) Заметим, что формула для расчета Eк похожа на выражение для определения кинетической энергии поступательного движения тела, только роль меры инертности в этом случае играет момент инерции, а не масса и характеристикой движения является угловая, а не линейная скорость твердого тела. Момент импульса
где Для нескольких частиц момент импульса определяется как (векторная) сумма таких членов:
где (В пределе количество частиц может быть бесконечным, например, в случае твердого тела с непрерывно распределенной массой или вообще распределенной системы это может быть записано как В системе СИ момент импульса измеряется в единицах джоуль-секунда; Дж·с. Из определения момента импульса следует его аддитивность: как, для системы частиц в частности, так и для системы, состоящей из нескольких подсистем, выполняется:
|
|||||||||
|
Последнее изменение этой страницы: 2016-09-13; просмотров: 346; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.189.171.137 (0.008 с.) |



 ,
, ,
,
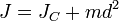

 можно расписать как разность двух векторов:
можно расписать как разность двух векторов: ,
, — радиус-вектор расстояния между старой и новой осью вращения. Тогда выражение для момента инерции примет вид:
— радиус-вектор расстояния между старой и новой осью вращения. Тогда выражение для момента инерции примет вид:




 частицы относительно некоторого начала отсчёта определяется векторным произведением её радиус-вектора и импульса:
частицы относительно некоторого начала отсчёта определяется векторным произведением её радиус-вектора и импульса:
 — радиус-вектор частицы относительно выбранного неподвижного в данной системе отсчёта начала отсчёта,
— радиус-вектор частицы относительно выбранного неподвижного в данной системе отсчёта начала отсчёта,  — импульс частицы.
— импульс частицы.
 — радиус-вектор и импульс каждой частицы, входящей в систему, момент импульса которой определяется.
— радиус-вектор и импульс каждой частицы, входящей в систему, момент импульса которой определяется. где
где  - импульс бесконечно малого точечного элемента системы).
- импульс бесконечно малого точечного элемента системы). .
.


