
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Необходимые сведения из теории.Содержание книги Поиск на нашем сайте
Средняя величина - это обобщающий показатель, который характеризует качественно однородную совокупность по определенному количественному признаку. Например, средний возраст лиц, осужденных за кражу. Средние величины бывают простые и взвешенные. Взвешенными средними называют величины, которые учитывают, что некоторые варианты значений признака могут иметь различную численность, в связи, с чем каждый вариант приходится умножать на соответствующую численность. Иными словами, «весами» выступают числа единиц совокупности в разных группах, т.е. каждый вариант «взвешивают» по своей частоте. Частоту называют статистическим весом. Средняя арифметическая простая – самый распространенный вид средней. Она равна сумме отдельных значений признака, деленной на общее число этих значений:
где x1,x2, …,xN – индивидуальные значения варьирующего признака (варианты), а N – число единиц совокупности. Средняя арифметическая взвешенная применяется в тех случаях, когда данные представлены в виде рядов распределения или группировок. Она вычисляется как сумма произведений вариантов на соответствующие им частоты, деленная на сумму частот всех вариантов:
где xi – значение i–й варианты признака; fi – частота i–й варианты. Таким образом, каждое значение варианты взвешивается по своей частоте, поэтому частоты иногда называют статистическими весами. Замечание. Если вычисление средней величины производят по данным, сгруппированным в виде интервальных рядов распределения, то сначала надо определить серединные значения каждого интервала х'i, после чего рассчитать среднюю величину по формуле средней арифметической взвешенной, где вместо xi используется х'i. Вариация – это различия в значениях какого-либо признака у разных единиц данной совокупности в один и тот же период или момент времени. Она возникает в результате того, что индивидуальные значения признака складываются под совокупным влиянием разнообразных факторов (условий), которые по-разному сочетаются в каждом отдельном случае. Показатели вариации используются для установления типичности средней величины, т. е. насколько точно характеризует средняя данную совокупность по определенному признаку. К основным показателям вариации относятся следующие:
1) дисперсия; 2) среднее квадратическое отклонение; 3) коэффициент вариации. Дисперсия определяется как средняя из отклонений, возведенных в квадрат. Простая дисперсия для не сгруппированных данных:
Взвешенная дисперсия для вариационного ряда:
Замечание. На практике для вычисления дисперсии лучше использовать следующие формулы: Для простой дисперсии
Для взвешенной дисперсии Среднее квадратическое отклонение - это корень квадратный из дисперсии:
Среднее квадратическое отклонение является мерилом надежности средней. Чем меньше среднее квадратическое отклонение, тем, однороднее совокупность и тем лучше средняя арифметическая отражает собой всю совокупность. Коэффициент вариации – выраженное в процентах отношение среднего квадратического отклонения к средней арифметической:
Коэффициент вариации используют не только для сравнительной оценки вариации разных признаков или одного и того же признака в различных совокупностях, но и для характеристики однородности совокупности. Статистическая совокупность считается количественно однородной, если коэффициент вариации не превышает 33 % (для распределений, близких к нормальному распределению). Порядок работы
1 Открыть новый файл в приложении MS Excel и сохранить файл, указав в имени файла свою фамилию. Создать в Excel таблицу 5 и добавить к ней справа 4 столбца: «Дисперсия срока лишения свободы», «Медиана срока лишения свободы», «Мода срока лишения свободы», «Среднее квадратическое отклонение» и «Коэффициент вариации».
Формула исчисления медианы для интервального вариационного ряда имеет следующий вид:
Ме = ХМе + iМе * (∑f/2 - SМе-1)/fМе, Где ХМе - начальное значение медианного интервала; iМе - величина медианного интервала; ∑f - сумма частот ряда (численность ряда); SМе-1 - сумма накопленных частот в интервалах, предшествующих медианному; fМе - частота медианного интервала.
Для расчета определенного значения модальной величины признака, заключенного в интервале, применяют формулу: Мо = ХМо + iМо *(fМо - fМо-1)/((fМо - fМо-1) + (fМо - fМо+1)), Где ХМо - минимальная граница модального интервала; iМо - величина модального интервала; fМо - частота модального интервала; fМо-1 - частота интервала, предшествующего модальному; fМо+1 - частота интервала, следующего за модальным.
10. Сделайте вывод об однородности статистических совокупностей, используя полученные значения коэффициента вариации. 11. Постройте диаграмму с графиками, отражающими распределение числа осужденных за преступления различной степени тяжести по срокам лишения свободы. 12. Исключите из расчетов число осужденных, которым были назначены в итоговом наказании сроки лишения свободы, превышающие верхний предел по тяжести, предусмотренный ст. 15 УК РФ (в редакции, соответствующей 2008 году). Произведите в дополнительных столбцах пересчет рассчитанных средних значений и показателей вариации, Сравните полученные результаты. Задание для компьютерного практикума по теме «Ряды динамики». Цель: Освоить расчет показателей динамики, научиться строить графики динамики судимости и линии тренда, строить прогноз. Задачи: 1. Произвести расчеты показателей динамики, используя средства приложения MS Office табличного процессора Excel.
2. Построить график динамики судимости и провести выравнивание ряда динамики с помощью скользящей средней. 3. Построить линию тренда и сделать прогноз на год вперед. Исходные статистические данные. Таблица 6.
За 2011 г. данные с учетом военных судов
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 422; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.137.176.238 (0.01 с.) |

 ,
, ,
,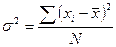 .
.
 .
.
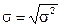
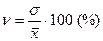
 , вычисленный на четвертом этапе работы. Протяните формулу по всем строкам – для всех категорий и общего числа осужденных (не забудьте зафиксировать адреса ячеек, ссылающиеся на середины интервалов знаком $).
, вычисленный на четвертом этапе работы. Протяните формулу по всем строкам – для всех категорий и общего числа осужденных (не забудьте зафиксировать адреса ячеек, ссылающиеся на середины интервалов знаком $).


