
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Цикл Карно обратим, так как все его составные части являются равновесными процессами.Содержание книги
Поиск на нашем сайте
Приведенные выше рассуждения позволяют перейти к формулировке первой и второй теорем Карно. Их можно сформулировать в виде двух следующих утверждений: 1. Коэффициент полезного действия любой обратимой тепловой машины, работающей по циклу Карно, не зависит от природы рабочего тела и устройства машины, а является функцией только температуры нагревателя
2. Коэффициент полезного действия любой тепловой машины, работающей по необратимому циклу, меньше коэффициента полезного действия машины с обратимым циклом Карно, при условии равенства температур их нагревателей и холодильников:
35. Второе начало термодинамики может быть сформулировано несколькими способами. В наиболее очевидной формулировке второе начало гласит, что невозможен самопроизвольный переход тепла от тела, менее нагретого, к телу, более нагретому. Более строго, невозможны такие процессы, единственным конечным результатом которых был бы переход тепла от тела, менее нагретого, к телу, более нагретому. Второе начало термодинамики может быть также сформулировано следующим образом: невозможны такие процессы, единственным конечным результатом которых явилось бы отнятие от некоторого тела определенного количества тепла и превращения этого тепла полностью в работу. На первый взгляд может показаться, что второй формулировке противоречит, например, процесс изотермического расширения идеального газа. Действительно, все полученное идеальным газом от какого-то тела тепло превращается полностью в работу. Однако получение и превращение его в работу не единственный конечный результат процесса, кроме того, в результате происходит изменение объема газа. Легко убедиться, что утверждение, содержащееся во второй формулировке, логически вытекает из утверждения, заключенного в первой формулировке. В самом деле, работа может быть полностью превращена в тепло, например, при трении. Поэтому, превратив с помощью процесса, запрещенного второй формулировкой, тепло, отнятое от какого-либо тела, полностью в работу, а затем превратив эту работу при посредстве трения в тепло, сообщаемое другому телу с более высокой температурой, мы осуществим процесс, невозможный согласно первой формулировке.
Использую процессы, запрещаемые вторым началом термодинамики, можно было бы создать двигатель, совершающий работу за счет тепла, получаемого от такого, например, практически неисчерпаемого источника энергии, как океан. Практически такой двигатель был бы равнозначен вечному двигателю. Поэтому второе начало иногда формулируется следующим образом: невозможен перпетуум мобиле второго рода, т.е. такой периодически действующий двигатель, который получал бы тепло от одного резервуара и превращал это тепло полностью в работу.
36. Неравенство Клаузиуса (1854): Количество теплоты, полученное системой при любом круговом процессе, делённое на абсолютную температуру, при которой оно было получено (приведённое количество теплоты), неположительно.
Подведённое количество теплоты, квазистатически полученное системой, не зависит от пути перехода (определяется лишь начальным и конечным состояниями системы) - для квазистатических процессов неравенство Клаузиуса обращается в равенство [1] .
\Отношение Q / T называется приведённой теплотой.
37. Энтропи́я (от др.-греч. ἐντροπία - поворот, превращение) — в естественных науках мера беспорядка системы, состоящей из многих элементов. В частности, в статистической физике — меравероятности осуществления какого-либо макроскопического состояния; в теории информации — мера неопределённости какого-либо опыта (испытания), который может иметь разные исходы, а значит, и количество информации; в исторической науке, для экспликациифеномена альтернативности истории (инвариантности и вариативности исторического процесса). Другая формулировка второго начала термодинамики основывается на понятии энтропии: · «Энтропия изолированной системы не может уменьшаться» (закон неубывания энтропии). Такая формулировка основывается на представлении об энтропии как о функции состояния системы, что также должно быть постулировано. Второе начало термодинамики в аксиоматической формулировке Рудольфа Юлиуса Клаузиуса (R. J. Clausius, 1865) имеет следующий вид [2] : Для любой квазиравновесной термодинамической системы существует однозначная функция термодинамического состояния
38. аким образом, изменение энтропии ΔS1-2 идеального газа при переходе его из состояния 1 в состояние 2 не зависит от вида перехода 1 - 2.
изотермический:
39. адиабатический:
Удельную энтропию можно применять совместно с одним из основных параметров для графического изображения процессов. Аналогично тому, как мы строили изменение объема в зависимости от изменения температуры, мы можем изобразить некоторый процесс изменения энтропии и температуры в Т-S координатах. В этом случае любая точка на графической плоскости соответствует определенному состоянию рабочего тела, а линия от точки 1 до точки 2 отображает некий термодинамический процесс. Особенностью Т-S координат является то, что площадь под линией процесса соответствует количеству энергии отданной или полученной рабочим телом.
На данной диаграмме представлен некий замкнутый цикл. Система последовательно переходит из точки 1 в 2 затем 3, 4 и снова в 1. Из графика видно что процесс 1® 2 является изотермическим (происходит при Т1) и процесс 3® 4 также является изотермическим (происходит при T2) Процессы 2® 3 и 4® 1 являются адиабатными. Поскольку в них не происходит изменение энтропии то dS = 0 следовательно dQ = 0 или Q = const. 40. Третье начало термодинамики (теорема Нернста) — физический принцип, определяющий поведение энтропии при приближении температуры к абсолютному нулю. Является одним из постулатовтермодинамики, принимаемым на основе обобщения значительного количества экспериментальных данных. Третье начало термодинамики может быть сформулировано так: «Приращение энтропии при абсолютном нуле температуры стремится к конечному пределу, не зависящему от того, в каком равновесном состоянии находится система».
или
где Следствия
|
|||||||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 401; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.139.119 (0.01 с.) |

 и холодильника
и холодильника  :
: ;
;
 .
.


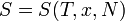 , называемая энтропией, такая, что ее полный дифференциал
, называемая энтропией, такая, что ее полный дифференциал  .
. , т.к.
, т.к.  ;
;  т.к.
т.к. 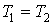 ;
; , т.к.
, т.к. 


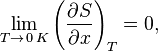
 — любой термодинамический параметр.
— любой термодинамический параметр.


