
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Цепи с распределенными параметрами. Типы линии передач.Содержание книги
Поиск на нашем сайте Если по всей длине линии связи или линии передачи, значение индуктивности, активного сопротивления, емкости и проводимости распределены равномерно и данные условия выполняются, то ее мы называем цепью с распределенными параметрами. Линия передачи -протяжённое на всём расстоянии от точки передачи до точки приёма устройство, ограничивающее область распространения электромагнитных колебаний и направляющее поток электромагнитной энергии в заданном направлении. Основные типы линии передач: 1.Длинные линии. Длинная линия -регулярная линия электропередачи, длина которой превышает длину волны колебаний, распространяющихся в ней, а расстояние между проводниками, из которых она состоит, значительно меньше этой длины волны. 2.Волноводы. Волновод - канал, способный поддерживать распространяющиеся вдоль него волны, поля которых сосредоточены внутри канала или в примыкающей к нему области. 3.Линии передачи поверхностных волн, в которых распространяются волны смешанного типа(диэлектрические волноводы). 4.Лучеводы, оптические линии передач. Лучевод -особый вид волновода, квазиоптическая линия передачи, служащая для распространения волн миллиметрового и субмиллиметрового диапазона. 5.Линия Губо. Однопроводная линия передачи высоких частот, представляющая собой металлический проводник, окруженный слоем диэлектрика 6.Полосковая линия. Линия передачи СВЧ, представляет собой радиоволновод для передачи электромагнитных волн в воздушной или иной диэлектрической среде вдоль двух или нескольких проводников, имеющих форму тонких полосок и пластин. Они бывают симметричными и несимметричными. 7.Коаксильный кабель. Кабель служащий для передачи высокочастотных сигналов.
Однородная линия при гармоническом внешнем воздействии. Телеграфные уравнения. Решение уравнений Гельмгольца. Цепями с распределенными параметрами называются идеализированные электрические цепи, процессы в которых описываются дифференциальными уравнениями в частных производных. Токи и напряжения в одномерной цепи с распределенными параметрами являются функциями двух переменных – времени t и координаты x. Первыми в качестве одномерных цепей с распределенными параметрами стали представлять так называемые длинные линии, т.е. линии передачи энергии от источника к нагрузке, длина которых значительно превышает длину волны передаваемых электромагнитных колебаний. Поэтому одномерные цепи с распределенными параметрами часто называют длинными линиями или линиями, а уравнения (1) и (2), описывающие зависимости между токами и напряжениями элементарного участка одномерной цепи с распределенными параметрами,– дифференциальными уравнениями длиной линии или телеграфными уравнениями.
где G1 , C1, R1 ,L1 – первичные параметры линии (погонные параметры). Они называются телеграфными, т.к. первоначально были получены в теории телеграфной связи. Распределения комплексных действующих значений напряжения U(x) и тока I(x)в однородной длинной линии, находящейся под гармоническим внешним воздействием, определяются выражениями
Входящий в выражения комплексный коэффициент распространения и комплексное волновое сопротивление Решение уравнений Гельмгольца. Преобразовывая телеграфные уравнение, сможем получить уравнения Гельмгольца. Используя положения символического метода анализа (законы Ома и Кирхгофа для комплексных амплитуд или комплексных действующих значений токов и напряжений), преобразуем уравнения (1) и (2) к следующему виду:
Так как комплексы I(х) и U(х) являются функциями только одной переменной х, то уравнения (1), (2) записываются в полных производных. Для решения системы (3) продифференцируем по х первое уравнение и подставим в него второе. Тогда получим:
где
|
||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 874; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.009 с.) |

 (1)
(1) (2),
(2), и
и 

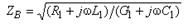 называются коэффициентом распространения и волновым сопротивлением линии.
называются коэффициентом распространения и волновым сопротивлением линии. ,
, (3)
(3) (1-e уравнение Гельмгольца),
(1-e уравнение Гельмгольца), (2-e уравнение Гельмгольца),
(2-e уравнение Гельмгольца), – погонное комплексное сопротивление,
– погонное комплексное сопротивление,  - погонная комплексная проводимость.
- погонная комплексная проводимость.


