
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Модель мінімізації залишків незавершеного виробництваСодержание книги
Поиск на нашем сайте
Для кожного інтервалу часу t відомий попит на продукт
Якщо зростання, то
10. Виробни́ча функція. Види виробничих функцій. 10 Виробни́ча фу́нкція — залежність кінцевого виходу продукції чи її вартості від використання різних факторів виробництва, конкретних видів ресурсів і затрат, подана в математичній формі. Як правило, застосовують прості функції з однією або кількома змінними — лінійну, квадратичну, степеневу, показникову, гіперболічну тощо. Найзагальніший вигляд виробничої функції: Q = f(K, L) де Q — обсяг виробництва; K — обсяг капіталу; L — обсяг праці Функція Кобба-Дугласа має вигляд: Q=A,Kб,Lв, (2) де А - коефіцієнт пропорційності або масштабності; б, в - коефіцієнти еластичності виробництва, які характеризують приріст обсягів виробництва при прирості відповідних факторів на 1%. Розрахунки показали, що за досліджуваний період коефіцієнти функції мають значення: A=1,01; а = 1/4; в=3/4. Тобто функція приймає вид: Q=1,01K1/4 L3/4 З цього випливає, що найважливішим фактором виробництва є праця, яка дає приріст виробництва 3/4 проти капіталу, який дає 1/4 приросту, тобто збільшення витрат праці на 1 % розширює обсяги виробництва в 3 рази більше, ніж відповідне збільшення капіталу. Пізніше у функцію виробництва вчені ввели фактор часу і якісні зміни в процесі виробництва, перейшовши від статичної моделі Кобба-Дугласа до динамічної моделі: Q=A Kб Lв ert, де ert - фактор, що відображає вплив технічного прогресу й інших якісних змін у виробництві протягом певного часу. · Функція з фіксованими пропорціями чинників (функція Леонтьєва).
· Лінійна функція
· Функція Аллена:
· Функція постійної еластичності заміщення чинників (функція CES):
· Функція Солоу:
· Багаторежимна функція:
11. Цільова функція споживання і моделювання поведінки споживачів. Рівень задоволення матеріальних потреб суспільства (рівень споживання) можна виразити цільовою функцією споживання U = U (Y), де вектор змінних Y >= 0 включає різноманітні види товарів і послуг. Ряд властивостей цієї функції зручно вивчати, використовуючи геометричну інтерпретацію рівнянь U (Y) = С, де С — параметр, що характеризує значення (рівень) цільової функції споживання; як величина С може виступати, наприклад, прибуток або рівень матеріального добробуту. Функції купівельного попиту — це функції, що відображають залежність обсягу попиту на окремі товари і послуги від комплексу фактів, що впливають на нього. Такі функції застосовуються в аналітичних моделях попиту і споживання і будуються на основі інформації про структуру прибутків населення, ціни на товари, склад сімей та інші фактори. Розглянемо побудову функцій попиту залежно від двох факторів: доходу і цін. Однофакторні функції попиту від доходу широко застосовуються при аналізі купівельного попиту yi = fі (Z), де Z — доход; yi — попит на і -й товар або послугу; fі — тип функції. Відповідні цим функціям криві називаються кривими Ангеля. Той самий принцип розмежування груп товарів по типах функцій попиту від доходу використав шведський економіст Л. Торнквіст, який запропонував спеціальні види функцій попиту (функції Торнквіста) для трьох груп товарів: першої необхідності, другої необхідності, предметів розкоші. Функція Торнквіста для товарів першої необхідності Y 1 має такий вигляд: Y 1 = a 1 Z / (Z + C 1), (3.3) де а 1 — верхня межа попиту; С 1 — приріст доходу. Вона відображає той факт, що зростання попиту на ці першочергові товари зі зростанням доходу поступово сповільнюється і має межу a 1(крива попиту асимптотично наближується до прямої лінії у = а 1). Функція Торнквіста для товарів другої необхідності Y 2 має такий вигляд: Y 2 = a 2 (Z – b 2) / (Z + C 2), (3.4) де Z? b 2; а 2 — верхня межа попиту; b 2 — певний рівень доходу; С 2 — приріст доходу. Попит на цю групу товарів з’являється після того, як дохід досягне величини b 2 Функція Торнквіста для предметів розкоші Y 3 має такий вигляд: Y 3 = a 3 Z (Z – b 3) / (z + C 3), (3.5) де Z? b 3; a 3 >1; b 3— певний рівень доходу; C 3— приріст доходу. Функція Y 3 не має межі, попит на предмети розкоші виникає після того, як дохід Z перевищить рівень b 3. Графіки цих функцій наведено на рис. 3.1.
Крім розглянутих функцій, в аналітичних моделях купівельного попиту використовуються й інші функції — степеневі, S -подібні та ін. Важливу роль в аналізі попиту відіграють коефіцієнти еластичності, які визначають, на скільки відсотків зміниться попит, якщо дохід зміниться на 1 %:
Зокрема, застосовуючи (3.6) до функції Торнквіста (3.3.), отримуємо коефіцієнт еластичності:
Коефіцієнт еластичності для функції (3.5):
У товарах еластичного попиту підвищення ціни на 1 % призводить до зниження попиту більш як на 1 %, і навпаки, пониження ціни на 1 % приводить до зростання купівлі більше як на 1 %. Якщо підвищення ціни на 1 % спричиняє зниження попиту менш як на 1 %, то кажуть, що це — товар нееластичного попиту.
|
||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 230; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.189.141.63 (0.011 с.) |

 і відомий початковий запас продукції
і відомий початковий запас продукції  і запас продукції на кінець періоду t –
і запас продукції на кінець періоду t –  . Величина
. Величина 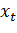 – випуск продукції в t інтервалі і є шуканою величиною –
– випуск продукції в t інтервалі і є шуканою величиною –  . Для виробництва важлива розмірність, тому
. Для виробництва важлива розмірність, тому  в інтервалах не повинно змінюватися;
в інтервалах не повинно змінюватися;  – зростання виробництва,
– зростання виробництва,  – зниження виробництва.
– зниження виробництва.
 і навпаки – спадання. Задача мінімізації залишків незавершеного виробництва має вигляд:
і навпаки – спадання. Задача мінімізації залишків незавершеного виробництва має вигляд: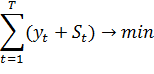

 – попит.
– попит.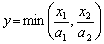 , (5.1) де а 1, а 2 — параметри. Відомо кілька альтернативних систем (гіпотез), що виокремлюють функції цього виду: функція є розв’язком такої задачі математичного програмування; функція є однорідною, а еластичність заміни чинників дорівнює нулю; Функція Леонтьєва призначена в основному для моделювання строго детермінованих технологій, які не допускають відхилення від технологічних норм і нормативів щодо використання ресурсів на одиницю продукції. Як правило, вона використовується для формалізованого опису дрібномасштабних або цілком автоматизованих об’єктів.
, (5.1) де а 1, а 2 — параметри. Відомо кілька альтернативних систем (гіпотез), що виокремлюють функції цього виду: функція є розв’язком такої задачі математичного програмування; функція є однорідною, а еластичність заміни чинників дорівнює нулю; Функція Леонтьєва призначена в основному для моделювання строго детермінованих технологій, які не допускають відхилення від технологічних норм і нормативів щодо використання ресурсів на одиницю продукції. Як правило, вона використовується для формалізованого опису дрібномасштабних або цілком автоматизованих об’єктів. . (5.3) Передумови та гіпотези: в) функція однорідна, й еластичність заміни чинників, за Алленом, є нескінченною; г) еластичність випуску за чинниками обернено пропорційна їхній середній продуктивності. Лінійна функція застосовується для моделювання великомасштабних систем (велика галузь, народне господарство в цілому), у яких випуск продукції є результатом одночасного функціонування великої кількості різноманітних технологій. Особливу роль відіграє гіпотеза постійності граничних виробничих чинників чи їх необмеженого заміщення.
. (5.3) Передумови та гіпотези: в) функція однорідна, й еластичність заміни чинників, за Алленом, є нескінченною; г) еластичність випуску за чинниками обернено пропорційна їхній середній продуктивності. Лінійна функція застосовується для моделювання великомасштабних систем (велика галузь, народне господарство в цілому), у яких випуск продукції є результатом одночасного функціонування великої кількості різноманітних технологій. Особливу роль відіграє гіпотеза постійності граничних виробничих чинників чи їх необмеженого заміщення. (5.4) визначається за такими умовами: швидкості зростання граничних продуктивностей є постійними, і функція є однорідною. Функція Аллена за a 1, a 2 > 0 призначається для формалізованого опису виробничих процесів, у яких надмірне зростання будь-якого з чинників негативно впливає на обсяг випуску продукції. Зазвичай така функція використовується для формалізованого опису дрібномасштабних виробничих систем з обмеженими можливостями переробки ресурсів.
(5.4) визначається за такими умовами: швидкості зростання граничних продуктивностей є постійними, і функція є однорідною. Функція Аллена за a 1, a 2 > 0 призначається для формалізованого опису виробничих процесів, у яких надмірне зростання будь-якого з чинників негативно впливає на обсяг випуску продукції. Зазвичай така функція використовується для формалізованого опису дрібномасштабних виробничих систем з обмеженими можливостями переробки ресурсів. (5.5) Передумови та гіпотези: Функція є однорідною, й еластичність заміщення чинників є постійною. Функція CES застосовується у разі відсутності точної інформації щодо рівня взаємозаміни виробничих чинників, і разом з тим є підстави вважати, що цей рівень суттєво не зміниться за зміни обсягів залучених ресурсів, тобто коли економічна технологія має властивість певної стійкості щодо певних пропорцій чинників. Функція CES (за наявності засобів оцінки її параметрів) може використовуватись для моделювання систем будь-якого рівня.
(5.5) Передумови та гіпотези: Функція є однорідною, й еластичність заміщення чинників є постійною. Функція CES застосовується у разі відсутності точної інформації щодо рівня взаємозаміни виробничих чинників, і разом з тим є підстави вважати, що цей рівень суттєво не зміниться за зміни обсягів залучених ресурсів, тобто коли економічна технологія має властивість певної стійкості щодо певних пропорцій чинників. Функція CES (за наявності засобів оцінки її параметрів) може використовуватись для моделювання систем будь-якого рівня. (5.6) характеризується тим, що величина відсоткової зміни граничної норми заміщення чинників, що пов’язане зі зміною одного з чинників на один відсоток, не залежить від початкового рівня чинників. Дана функція може використовуватись приблизно в тих самих ситуаціях, що й функція CES. Функція Солоу може використовуватись у моделюванні системи різних масштабів.
(5.6) характеризується тим, що величина відсоткової зміни граничної норми заміщення чинників, що пов’язане зі зміною одного з чинників на один відсоток, не залежить від початкового рівня чинників. Дана функція може використовуватись приблизно в тих самих ситуаціях, що й функція CES. Функція Солоу може використовуватись у моделюванні системи різних масштабів.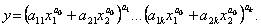 (5.7) Багаторежимна функція — одна з найзагальніших. Вона використовується для формалізованого опису та моделювання процесів, у яких рівень віддачі кожної додаткової одиниці ресурсу стрибкоподібно змінюється залежно від співвідношення чинників. Функцію доцільно застосовувати за наявності апріорної інформації щодо кількості режимів k, а інколи й щодо величини «перехідної» області між режимами (чим більше
(5.7) Багаторежимна функція — одна з найзагальніших. Вона використовується для формалізованого опису та моделювання процесів, у яких рівень віддачі кожної додаткової одиниці ресурсу стрибкоподібно змінюється залежно від співвідношення чинників. Функцію доцільно застосовувати за наявності апріорної інформації щодо кількості режимів k, а інколи й щодо величини «перехідної» області між режимами (чим більше  , тим чіткіше виокремлюються режими).
, тим чіткіше виокремлюються режими). Рис. 3.1. Функції Торнквіста
Рис. 3.1. Функції Торнквіста , де
, де 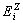 — коефіцієнт еластичності для і -ї групи товарів відносно доходу Z; yі — попит на і -ту групу товарів.
— коефіцієнт еластичності для і -ї групи товарів відносно доходу Z; yі — попит на і -ту групу товарів. . (3.3*) Коефіцієнт еластичності для функції (3.4):
. (3.3*) Коефіцієнт еластичності для функції (3.4):  . (3.4*)
. (3.4*) . (3.5*) У загальному випадку попит на окремий товар за інших рівних умов залежить від рівня цін на всі товари. Відносна зміна обсягу попиту за зміни ціни даного товару або цін інших пов’язаних з ним товарів характеризує коефіцієнт еластичності попиту від цін. Цей коефіцієнт еластичності зручно трактувати як величину зміни попиту в процентах за зміни ціни на 1 %.
. (3.5*) У загальному випадку попит на окремий товар за інших рівних умов залежить від рівня цін на всі товари. Відносна зміна обсягу попиту за зміни ціни даного товару або цін інших пов’язаних з ним товарів характеризує коефіцієнт еластичності попиту від цін. Цей коефіцієнт еластичності зручно трактувати як величину зміни попиту в процентах за зміни ціни на 1 %.


