Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Построение компьютерной модели бросания мячика в стенку в электронной таблице Microsoft ExcelСодержание книги
Поиск на нашем сайте
Рис.3. Содержательная постановка задачи В ячейку В1 вводим начальную скорость бросания мячика υo = 18 м/с,а значения четырех углов бросания 20°, 40°, 60° и 80° – соответственно в ячейки В2, D2, F2 и H2.
Рис.4. Условие задачи В ячейки А4:А21 ввести значения координаты мячика х с интервалом в 2 м. Для заданных значений координаты мячика х по формуле (3) вычислим значение времени t, апо формуле (2) координаты мячика у. В электронных таблицах аргументы функций COS() и SIN() задаются в радианах, поэтому необходимо преобразовать значения углов из градусов в радианы с помощью функции РАДИАНЫ().
Рис.5. Значения координат х с интервалом в 2 м Далее вводим ячейку В4 формулу =$A4/($B$1*COS(РАДИАНЫ(B2))) и в ячейку С4 формулу =$B$1*SIN(РАДИАНЫ(B2))*B4 – 4,9*B4*B4.
Рис6. Формула вычисления значения времени, t
Рис.7. Формула вычисления координаты мячика, y
Далее копируем введенные формулы в ячейки D4, F4, H4, и E4, G4, I4 соответственно. Затем устанавливаем в формулах абсолютные ссылки на ячейки $B$2, $D$2, $F$2, $H$2.
Рис.8. Абсолютная ссылка на ячейку B1-начальную скорость бросания мячика и B2-Угол бросания 20 градусов для значения времени, t
Рис.9. Абсолютная ссылка на ячейку B1-начальную скорость бросания мячика и B2-Угол бросания 20 градусов для координат мячика, у Аналогично устанавливаем в формулах абсолютные ссылки на ячейки $D$2, $F$2, $H$2. Далее выделяем диапазон ячеек В4:I4 и, используя маркер заполнения, скопировать его в диапазон ячеек В5:I21. В столбцах С, D, F и H получаем координаты мячика по оси У для четырех углов бросания, соответствующие значениям координаты мячика по оси X, указанным в столбце А, которые показаны на рисунке 10.
Рис.10. Координаты движения мячика для четырех углов бросания Визуализируем модель, построив графики зависимости координаты у от координаты х (траекторию движения мячика) для четырех углов бросания. Для построения траектории движения мячика используем диаграмму типа График. При построении графика в качестве категорий используем диапазон ячеек А4:А21, а в качестве значений – диапазоны ячеек С4:С21, Е4:Е21, G4:G21, I4:I21
Далееисследуем модель и определим с заданной точностью (например, 0,1°) диапазон углов бросания, которые обеспечивают попадание мячика в стенку.
В качестве начальных условий бросания мячика выберем, например, следующие: скорость бросания υo = 18 м/с, высота стенки h = 1 м, расстояние до стенки s = 30 м, значение угла бросания α = 40°. Затем, заполняем ячейки с текстовой информацией. Вводим: • в ячейку В23 – значение расстояния до стенки; • в ячейку В24 – значение начальной скорости; • в ячейку В25 – значение угла бросания; • в ячейку В27 – формулу для вычисления высоты мячика в момент попадания в стенку для заданных начальных условий: = B23*TAN(РАДИАНЫ(B25))-(9,81*B23^2)/(2*B24^2*COS(РАДИАНЫ(B25))^2)
Рис.12. Определение диапазона углов методом Подбор параметров Для заданных начальных условий (скорости бросания и расстояния до стенки) проведем поиск углов, которые дают попадание в стенку на высотах 0 и 1 м. Используем для этого метод Подбор параметра. Надстройка Подбор параметра в электронных таблицах Microsoft Excel установлена по умолчанию. Методом Подбор параметра будем сначала искать значение угла бросания, которое обеспечит попадание мячика в стенку на минимальной высоте 0 метров. В данном случае значение функции (высота мячика при попадании в стенку) хранится в ячейке В27 (см. рис. 12), а значение аргумента (угла бросания) – в ячейке В25. Значит, необходимо установить в ячейке В27 значение 0 и методом Подбор параметра найти соответствующее значение аргумента в ячейке В25. Выделить ячейку В27, содержащую значение высоты мячика, и ввести команду [Сервис-Подбор параметра…]. В появившемся диалоговом окне (рис. 13) ввести в поле Значение: наименьшую высоту попадания в стенку (т. е. 0). В поле Изменяя значение ячейки: ввести адрес ячейки $В$25, содержащей значение угла бросания. Щелкнуть по кнопке ОК.
Рис.13. Ввод данных для метода Подбор данных В ячейке В25 появится значение 32,6, т. е. минимальное значение угла бросания мячика, которое обеспечивает попадание в стенку при заданных начальных условиях.
Рис.14. Определение диапазона углов методом Подбор параметра Методом Подбор параметра найдем теперь угол бросания, который обеспечит попадание мячика в стенку на максимальной высоте 1 метр. Выделить ячейку В27, содержащую значение высоты мячика, и ввести команду [Сервис-Подбор параметра...].
В появившемся диалоговом окне ввести в поле Значение: наибольшую высоту попадания в стенку (т. е. 1). В поле Изменяя значение ячейки: ввести адрес ячейки $В$25, содержащей значение угла бросания. Щелкнуть по кнопке ОК.
Рис.15. Ввод данных для метода Подбор данных В ячейке В25 появится значение 36,1, т. е. максимальное значение угла бросания мячика, которое обеспечивает попадание в стенку при заданных начальных условиях.
Рис.16. Определение диапазона углов методом Подбор параметра Аналогично повторим процедуру определения диапазона углов при начальном значении угла в ячейке В25, равном 60°. Получим значения предельных углов 55,8° и 57,4°, т. е. второй диапазон углов. Ввести полученные значения углов 32,6°, 36,1°, 55,8° и 57,4° соответственно в ячейки B2, D2, F2 и H2. На диаграмме можно проследить за изменением траекторий движения мячика на рисунке 17.
Рис.17. Координаты и траектории движения мячика для двух диапазонов углов бросания Анализ результатов. Исследование компьютерной модели в электронных таблицах показало: 1) при одинаковой начальной скорости мячик преодолевает большие расстояния при углах бросания в диапазоне от 20° до 80°; 2) существует два диапазона значений угла бросания мячика от 32,6° до 36,1° и от 55,8° до 57,4°, при которых обеспечивается попадание в стенку высотой 1 м, находящуюся на расстоянии 30 м, мячиком, брошенным со скоростью 18 м/с; 3) время, которое понадобится мячику, чтобы преодолеть расстояние до мишени увеличивается с возрастанием угла бросания. ЗАКЛЮЧЕНИЕ
Поставленная цель по созданию компьютерной модели тела, брошенного под углом к горизонту в электронных таблицах Microsoft Excel достигнута. Все задачи решены: 1. проведен анализ модели бросания мячика в стенку, расположенную на известном расстоянии с целью выявления параметров системы, необходимых для достижения поставленной цели, и связей между ними; 2. разработан процесс построения компьютерной модели физического процесса в электронных таблицах Microsoft Excel; 3. появилась возможность провести более точную оценку попадания мячика в стенку, расположенную на известном расстоянии, и проводить анализ траекторий его движения для нескольких углов бросания, построенных на одной диаграмме. По итогам произведенной работы выявлена актуальность использования электронных таблиц MicroSoft Excel для производства расчетов малой и средней сложности. В связи со скоростью разработки таблиц - шаблонов, простоты и понятности интерфейса, удобного вывода на печать, наличие широкого инструментария для вставки фильтров, поиска по таблице, возможности защитить документ от несанкционированного удаления данных, применения математических, физических, логических формул программа Excel подходит лучше всего. По проведенным тестам скорость обработки данных, удовлетворяет скорости нужной для обработки больших объемов информации, причем в удобной, визуально понятной форме. Программа MicroSoft Excel полностью справилась с решением поставленных задач по созданию таблицы для расчета движения тел. На основании проделанной работы можно сделать следующие выводы: 1. Решение физических задач с помощью табличного процессора Microsoft Excel намного проще и быстрее. 2. В электронных таблицах Microsoft Excel предоставляет пользователю множество возможностей. 3. В электронных таблицах Microsoft Excel имеется множество различных функций, упрощающих решение каких – либо задач из различных областей.
4. В электронных таблицах Microsoft Excel можно строить графики и диаграммы, с помощью которых можно наглядно показать результат решения. 5. Табличный процессор Microsoft Excel является удобным средством моделирования.
ЛИТЕРАТУРА
1. Э.В. Бурсиан. Физика. 100 задач для решения на компьютере. Учебное пособие. – СПб.: ИД «МиМ», 1997. 2. Угринович Н.Д. Исследование информационных моделей. Элективный курс: учебное пособие – М.: БИНОМ. Лаборатория знаний, 2006. 3. Угринович Н.Д. Информатика и информационные технологии: учебник для 10-11 классов – М.: БИНОМ. Лаборатория знаний, 2002. 4. Пак Н.И. Информатика. 2004. 5. Могилев А.В.Информатика. М.:Издательский центр «Академия».2003. 6. Леонтьев В.П. Новейшая энциклопедия персонального компьютера. 2003. 7. Кушнеренко А.Г.Основы информатики и вычислительной техники.М.:Просвещение.1991. 8. Кушнеренко А.Г.Новые информационные технологии.М.:Дрофа.2003. 9. Информатика. Энциклопедический словарь для начинающих. Под ред. 10. Информатика. Задачник-практикум. Т-2. под ред. И. Г. Семакина, 11. Е. К. Хеннера. М., Бином. Лаборатория Знаний, 2002 г 12. Д. А. Поспелова. М., Педагогика-Пресс 1994 г 13. http://www.alleng.ru/d/econ/econ271.htm 14. http://bourabai.kz/cm/index.htm ПРИЛОЖЕНИЯ
|
|||||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 2761; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.116.60.123 (0.011 с.) |









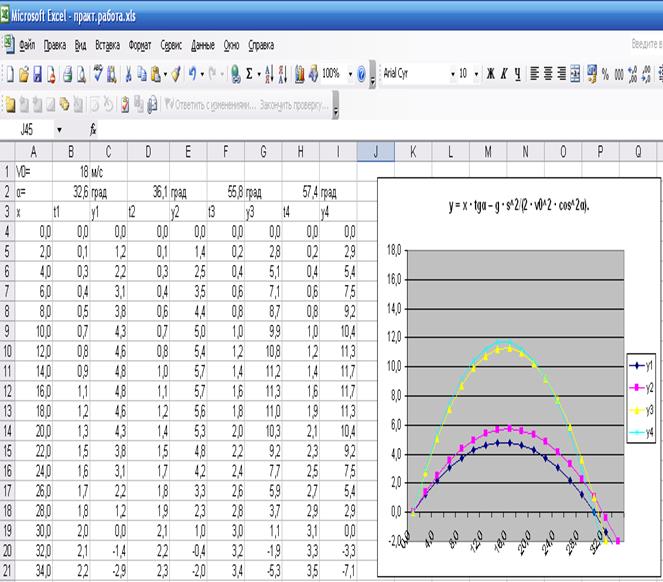
 Рис.11.Координаты и траектории движения мячика для четырех углов бросания
Рис.11.Координаты и траектории движения мячика для четырех углов бросания