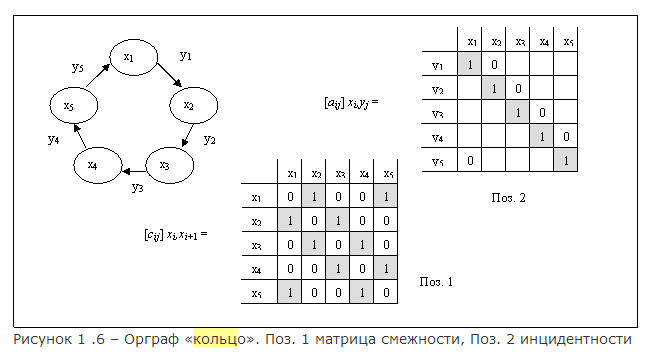
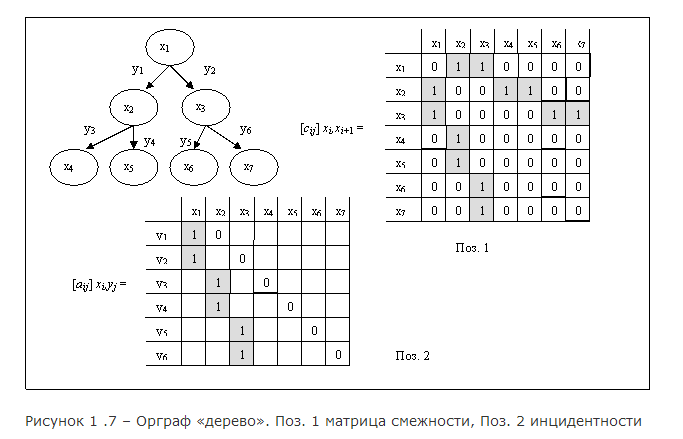
Матрицы смежности и инцидентности.

Организация графа.

Рассмотрим наиболее показательные условия соотношений множеств Yⁱⁿ { y_j } и Y^out { y_j }, устанавливающие организацию орграфа G.

1. Если для всякой вершины x_i∈X орграфа G выполняются условия: | Y ⁱⁿ { y_j }| = 1 и | Y^out { y_j }| = 1, то орграф представляет собой структуру в виде кольца. Данные условия обуславливают смежность и связность всех вершин орграфа.

2. Если для всякой вершины x_i∈X орграфа G выполняются условия: | Y ⁱⁿ { y_j } | ≠ ∅ и | Y ^out { y_j }| ≠ ∅, то такой граф является несвязанным. Если данные условия выполняются только для некоторых вершин, то орграф является частично связанным.

3. Если для всякой вершины x_i∈X орграфа G выполняются условия: | Y ⁱⁿ { y_j }| = 1 и | Y^out { y_j }| ≥ 1, то орграф представляет собой структуру в виде множества ветвей, расходящихся от корня дерева.

4. Если для всякой вершины x_i∈X орграфа G выполняются условия: | Y ⁱⁿ { y_j }| ≥ 1 и | Y^out { y_j }| = 1, то орграф представляет собой структуру в виде ветвей, сходящихся к корню дерева.

В случае 3 и 4 корень дерева может быть представлен в виде кольца. Кроме этого вершины всякой ветви орграфа (S^R) не связаны с вершинами иных ветвей.

Матрицы смежности и инцидентности.

Дополнительно организацию состояний можно отобразить с помощью матриц смежности и инцидентности [ 12-14 ]. Матрица смежности позволяет представить бинарные отношения между вершинами орграфа:

[ с_ij ] x_i, x_{i+ 1} = [ n X n ],

где: с_ij – отношения смежности выражают наличие дуг y_j между вершинами орграфа G;

n – количество строк и столбцов матрицы смежности (соответствует количеству x_i∈G).

Отношение смежности с_ij обозначается «1», если между вершинами x_i и x_{i+ 1}существует дуга y_j, иначе «0».

Матрица инцидентности позволяет представить отношения между количеством входящих и выходящих дуг некоторой вершины x_i∈G:

[ a_ij ] x_i,y_j = [ n X m ],

где: a_ij – отношение инцидентности дуги y_j к вершине x_i орграфа G;

n – количество строк вершин орграфа;

m – количество столбцов дуг орграфа.

Отношение a_ij обозначается «1», если дуга y_j выходит из вершины x_i, иначе «0» (если дуга y_j входит в вершину x_i).

На рисунках 1.6 – 1.8 представлены наиболее характерные варианты организации состояний в виде кольца, дерева (с одинаковым количеством «дочерних» вершин у всякого «родителя»), произвольного орграфа и соответствующие им матрицы смежности и инцидентности.

К 9. 10. 11.
· Всякое состояние характеризуется множеством родовых и видовых признаков.

· Родовые признаки, по сути, выделяют пространство состояний из множества состояний.

· Подмножество видовых признаков состояний выделяет всякое состояние пространства состояний.

· Пространство состояний включает в свой состав:

1) подмножество: S^o начальных состояний;

2) подмножество: S^t целевых состояний;

3) подмножество: S^с текущих состояний.

· В отличие от пространства состояний, пространство поиска -это всегда связная область.

· Представление пространства состояний в виде орграфа G= (X { x_i } ,Y { y_j }) позволяет выделить дополнительные свойства и организацию состояний:

1) если | Y ⁱⁿ { y_j }| = 1 и | Y^out { y_j }| = 1, то орграф представляет собой кольцо;

2) если | Yⁱⁿ { y_j }| = ∅ и | Y^out { y_j }| = ∅, то граф является несвязным;

3) если | Y ⁱⁿ { y_j } | = 1 и | Y^out { y_j }| ≥ 1, то орграф представляет собой расходящееся от корня дерево;

4) если | Y ⁱⁿ { y_j }| ≥ 1 и | Y ^out { y_j }| = 1, то орграф представляет собой сходящееся к корню дерево;

5) если | Y ⁱⁿ { y_j }| ≥ 1 и | Y^out { y_j }| = ∅, то вершина является терминальной;

6) если | Y ⁱⁿ { y_j }| =∅ и | Y ^out { y_j }| ≥ 1, то вершина является корневой.

· Матрица смежности позволяет представить бинарные отношения между вершинами орграфа.

· Матрица инцидентности позволяет представить отношения между количеством входящих и выходящих дуг вершин орграфа

Классификация МП.

Выделенные задачи позволяют разделить методы поиска на классы. Кроме этого, особенность разделения методов поиска на классы базируется на процедурах генерации, проверки, планирования, режимах поиска, позволяющих достичь того или иного результата в решении задач поиска состояния, расстояния, пути модели распределения и динамики состояний графа.Результат структурирования методов поиска на основе организации процедур и задач поиска представлен на рисунке 2.1 в виде классификации.

Слепые:
Особенность данного класса методов поиска заключается в том, что все процедуры выполняются последовательно и не зависят от результатов поиска.
Данные, получаемые в результате применения слепого метода поиска, практически не структурированы

На основе процедуры «проверка» выделяется класс «простейших эвристических методов поиска». Сущность методов заключается в том, что результаты проверки заносятся в память в виде апостериорной информации о состояниях анализируемого пространства. В дальнейшем эти данные позволяют управлять процедурой генерации.

Эвристические методы поиска на основе оценочной функции ориентированы на решение задачи выделения оптимального пути до целевого состояния пространства поиска. Особенностью представителей данного класса методов поиска является явно заданная эвристическая оценка, позволяющая выделить наиболее перспективное текущее решение и тем самым выделить оптимальный путь в пространстве состояний.

Организация графа.

Рассмотрим наиболее показательные условия соотношений множеств Yⁱⁿ { y_j } и Y^out { y_j }, устанавливающие организацию орграфа G.

1. Если для всякой вершины x_i∈X орграфа G выполняются условия: | Y ⁱⁿ { y_j }| = 1 и | Y^out { y_j }| = 1, то орграф представляет собой структуру в виде кольца. Данные условия обуславливают смежность и связность всех вершин орграфа.

2. Если для всякой вершины x_i∈X орграфа G выполняются условия: | Y ⁱⁿ { y_j } | ≠ ∅ и | Y ^out { y_j }| ≠ ∅, то такой граф является несвязанным. Если данные условия выполняются только для некоторых вершин, то орграф является частично связанным.

3. Если для всякой вершины x_i∈X орграфа G выполняются условия: | Y ⁱⁿ { y_j }| = 1 и | Y^out { y_j }| ≥ 1, то орграф представляет собой структуру в виде множества ветвей, расходящихся от корня дерева.

4. Если для всякой вершины x_i∈X орграфа G выполняются условия: | Y ⁱⁿ { y_j }| ≥ 1 и | Y^out { y_j }| = 1, то орграф представляет собой структуру в виде ветвей, сходящихся к корню дерева.

В случае 3 и 4 корень дерева может быть представлен в виде кольца. Кроме этого вершины всякой ветви орграфа (S^R) не связаны с вершинами иных ветвей.

Матрицы смежности и инцидентности.

Дополнительно организацию состояний можно отобразить с помощью матриц смежности и инцидентности [ 12-14 ]. Матрица смежности позволяет представить бинарные отношения между вершинами орграфа:

[ с_ij ] x_i, x_{i+ 1} = [ n X n ],

где: с_ij – отношения смежности выражают наличие дуг y_j между вершинами орграфа G;

n – количество строк и столбцов матрицы смежности (соответствует количеству x_i∈G).

Отношение смежности с_ij обозначается «1», если между вершинами x_i и x_{i+ 1}существует дуга y_j, иначе «0».

Матрица инцидентности позволяет представить отношения между количеством входящих и выходящих дуг некоторой вершины x_i∈G:

[ a_ij ] x_i,y_j = [ n X m ],

где: a_ij – отношение инцидентности дуги y_j к вершине x_i орграфа G;

n – количество строк вершин орграфа;

m – количество столбцов дуг орграфа.

Отношение a_ij обозначается «1», если дуга y_j выходит из вершины x_i, иначе «0» (если дуга y_j входит в вершину x_i).

На рисунках 1.6 – 1.8 представлены наиболее характерные варианты организации состояний в виде кольца, дерева (с одинаковым количеством «дочерних» вершин у всякого «родителя»), произвольного орграфа и соответствующие им матрицы смежности и инцидентности.

К 9. 10. 11.
· Всякое состояние характеризуется множеством родовых и видовых признаков.

· Родовые признаки, по сути, выделяют пространство состояний из множества состояний.

· Подмножество видовых признаков состояний выделяет всякое состояние пространства состояний.

· Пространство состояний включает в свой состав:

1) подмножество: S^o начальных состояний;

2) подмножество: S^t целевых состояний;

3) подмножество: S^с текущих состояний.

· В отличие от пространства состояний, пространство поиска -это всегда связная область.

· Представление пространства состояний в виде орграфа G= (X { x_i } ,Y { y_j }) позволяет выделить дополнительные свойства и организацию состояний:

1) если | Y ⁱⁿ { y_j }| = 1 и | Y^out { y_j }| = 1, то орграф представляет собой кольцо;

2) если | Yⁱⁿ { y_j }| = ∅ и | Y^out { y_j }| = ∅, то граф является несвязным;

3) если | Y ⁱⁿ { y_j } | = 1 и | Y^out { y_j }| ≥ 1, то орграф представляет собой расходящееся от корня дерево;

4) если | Y ⁱⁿ { y_j }| ≥ 1 и | Y ^out { y_j }| = 1, то орграф представляет собой сходящееся к корню дерево;

5) если | Y ⁱⁿ { y_j }| ≥ 1 и | Y^out { y_j }| = ∅, то вершина является терминальной;

6) если | Y ⁱⁿ { y_j }| =∅ и | Y ^out { y_j }| ≥ 1, то вершина является корневой.

· Матрица смежности позволяет представить бинарные отношения между вершинами орграфа.

· Матрица инцидентности позволяет представить отношения между количеством входящих и выходящих дуг вершин орграфа

Классификация МП.

Выделенные задачи позволяют разделить методы поиска на классы. Кроме этого, особенность разделения методов поиска на классы базируется на процедурах генерации, проверки, планирования, режимах поиска, позволяющих достичь того или иного результата в решении задач поиска состояния, расстояния, пути модели распределения и динамики состояний графа.Результат структурирования методов поиска на основе организации процедур и задач поиска представлен на рисунке 2.1 в виде классификации.

Слепые:
Особенность данного класса методов поиска заключается в том, что все процедуры выполняются последовательно и не зависят от результатов поиска.
Данные, получаемые в результате применения слепого метода поиска, практически не структурированы

На основе процедуры «проверка» выделяется класс «простейших эвристических методов поиска». Сущность методов заключается в том, что результаты проверки заносятся в память в виде апостериорной информации о состояниях анализируемого пространства. В дальнейшем эти данные позволяют управлять процедурой генерации.

Эвристические методы поиска на основе оценочной функции ориентированы на решение задачи выделения оптимального пути до целевого состояния пространства поиска. Особенностью представителей данного класса методов поиска является явно заданная эвристическая оценка, позволяющая выделить наиболее перспективное текущее решение и тем самым выделить оптимальный путь в пространстве состояний.

Познавательные статьи:



Формы дистанционного обучения

Передача мяча двумя руками снизу

Значение правильной осанки для жизнедеятельности человека

Основные ошибки при выполнении передач мяча на месте