Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Геометрическая аппроксимация заданной области (1-й этап мкэ)Содержание книги
Поиск на нашем сайте
МЕТОД КОНЕЧНЫХ ЭЛЕМЕНТОВ
МКЭ – это численный метод решения дифференциальных уравнений, сводящий дифференциальную задачу к системе линейных алгебраических уравнений на основе геометрической аппроксимации заданной области. МКЭ состоит из двух этапов: 1) геометрическая аппроксимация заданной области, 2) сведение на основе этапа 1 дифференциальной задачи к системе линейных алгебраических уравнений. МКЭ возник в связи с решением задач космических исследований в 50е годы XX столетия. С помощью МКЭ также решаются задачи распространения тепла, течения жидкостей, строительной механики и т.д. ГЕОМЕТРИЧЕСКАЯ АППРОКСИМАЦИЯ ЗАДАННОЙ ОБЛАСТИ (1-й этап МКЭ) 1. В заданной области, на которой определяется искомая величина, фиксируются точки – узлы будущей сетки. Значения искомой величины в узлах изначально неизвестны, и их определение является конечной целью решения дифференциальной задачи в МКЭ. 2. На основе выбранных узлов заданная область разбивается на подобласти, называемые элементами. Элементы в совокупности аппроксимируют форму области; при этом соседние элементы должны иметь общие узлы. 3. Искомая величина аппроксимируется на каждом элементе полиномом, называемым функцией элемента и определяемым с помощью узлов элемента. Т.о., любая непрерывная величина (температура, давление, концентрация) будет аппроксимирована дискретной моделью, состоящей из множества кусочно-непрерывных функций, каждая из которых описывает свой элемент. Преимущества и недостатки МКЭ Преимущества МКЭ. 1. МКЭ позволяет рассчитать приближённые значения искомой величины не только в узлах, но и в любой произвольной точке области (в отличие от метода разностных схем). 2. МКЭ позволяет задать аппроксимацию области с помощью криволинейных элементов, поэтому возможен расчёт областей сложной геометрической формы. 3. МКЭ позволяет задавать неравномерную сетку разбиения области на элементы, т.е. варьировать размеры элементов при необходимости. 4. Свойства материалов и толщина соседних элементов не должны быть одинаковыми, поэтому возможен расчёт сложных конструкций, составленных из разных материалов. 5. Возможно использование граничных условий с разрывной поверхностной нагрузкой.
Недостатки МКЭ. 1. Сложность математического обоснования. 2. Большое количество математических выкладок для получения конечного результата. 3. МКЭ предназначен для решения, главным образом, стационарных задач; решение нестационарных задач с помощью МКЭ представляет собой отдельную сложность.
Одномерные элементы
Двумерные элементы
Размеры элементов МКЭ допускает возможность варьирования размеров элементов. Уменьшение размеров элементов в некоторой части области может быть вызвано: 1) наличием криволинейной границы области, 2) наличием больших градиентов искомой величины. ОДНОМЕРНЫЙ СИМПЛЕКС-ЭЛЕМЕНТ
Одномерный СЭ представляет собой отрезок длины L с двумя узлами, расположенными на концах отрезка. Значения искомой величины в узлах обозначаем Ф1 и Ф2, значения в узлах координаты х, направленной вдоль элемента, – Х 1 и Х 2. Элемент описывается полиномом
коэффициенты которого могут быть определены с помощью узловых значений
Подставляя их в выражение полинома, получаем:
Таким образом, полином одномерного СЭ можно представить в виде:
Соотношение (1) позволяет рассчитать приближённое значение искомой величины φ в любой точке элемента при известных узловых значениях Ф1 , Ф2. Введём обозначения:
Функции N 1 и N 2 называют функциями формы. Каждая функция формы равна 1 в узле, к которому она относится, и равна 0 в другом узле:
Используя функции формы, запишем выражение (1) в виде:
Отметим, что функция элемента любого типа может быть представлена в данном виде.
ВТОРОЙ ЭТАП МКЭ Результатом 1-го этапа МКЭ будет геометрическая аппроксимация заданной области, т.е. задание узловых точек, элементов и описание искомой функции внутри каждого элемента с помощью функции элемента. Уравнение функции элемента любого типа можно представить в виде:
где функции формы содержат все особенности геометрии элемента, а узловые значения – неизвестные константы, определение которых является целью 2-го этапа МКЭ. Суть 2-го этапа МКЭ заключается в сведении исходной дифференциальной задачи к системе линейных алгебраических уравнений относительно узловых значений, в результате решения которой последние и будут найдены. Для этого используются разные методы, одним из которых является метод минимизации функционала, связанного с дифференциальным уравнением. Функционал – это функция, областью определения которой служит множество других функций. Вариация – это дифференциал функционала (обозначается символом δ). Рассмотрим функционал
Здесь F – некая функция внутреннего состояния системы, зависящая от x, y, z, φ, Основная задача вариационного исчисления состоит в том, чтобы найти такие функции F и G, чтобы при произвольном бесконечно малом их изменении величина функционала I оставалась постоянной:
Можно доказать, что это условие соответствует дифференциальному уравнению и граничным условиям относительно функций F и G:
где li – косинус угла, образованного нормалью к поверхности и i -й осью.
Постановка задачи
с граничными условиями
Здесь K – коэффициент теплопроводности материала стержня; тепловой поток q считается положительным, если тепло отводится от стержня в стену. МЕТОД КОНЕЧНЫХ ЭЛЕМЕНТОВ
МКЭ – это численный метод решения дифференциальных уравнений, сводящий дифференциальную задачу к системе линейных алгебраических уравнений на основе геометрической аппроксимации заданной области. МКЭ состоит из двух этапов: 1) геометрическая аппроксимация заданной области, 2) сведение на основе этапа 1 дифференциальной задачи к системе линейных алгебраических уравнений. МКЭ возник в связи с решением задач космических исследований в 50е годы XX столетия. С помощью МКЭ также решаются задачи распространения тепла, течения жидкостей, строительной механики и т.д. ГЕОМЕТРИЧЕСКАЯ АППРОКСИМАЦИЯ ЗАДАННОЙ ОБЛАСТИ (1-й этап МКЭ) 1. В заданной области, на которой определяется искомая величина, фиксируются точки – узлы будущей сетки. Значения искомой величины в узлах изначально неизвестны, и их определение является конечной целью решения дифференциальной задачи в МКЭ.
2. На основе выбранных узлов заданная область разбивается на подобласти, называемые элементами. Элементы в совокупности аппроксимируют форму области; при этом соседние элементы должны иметь общие узлы. 3. Искомая величина аппроксимируется на каждом элементе полиномом, называемым функцией элемента и определяемым с помощью узлов элемента. Т.о., любая непрерывная величина (температура, давление, концентрация) будет аппроксимирована дискретной моделью, состоящей из множества кусочно-непрерывных функций, каждая из которых описывает свой элемент.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 524; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.224.38.91 (0.01 с.) |












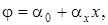
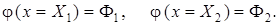
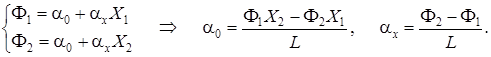
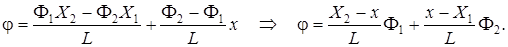 (1)
(1)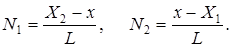
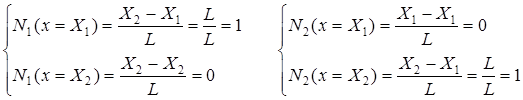
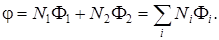 (2)
(2)

 ; G – функция внешней нагрузки на систему, которая может быть обусловлена массообменом и теплообменом с окружающей средой, а также воздействием сил различной природы на определённые точки границы области. Функционал I является определённым интегралом, поэтому при подстановке конкретных функций F и G он примет некоторое числовое значение.
; G – функция внешней нагрузки на систему, которая может быть обусловлена массообменом и теплообменом с окружающей средой, а также воздействием сил различной природы на определённые точки границы области. Функционал I является определённым интегралом, поэтому при подстановке конкретных функций F и G он примет некоторое числовое значение.
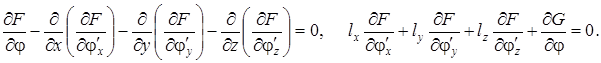
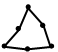
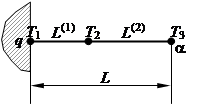 Рассмотрим стержень длиной L с теплоизолированной боковой поверхностью, один из концов которого закреплён в стене. Площадь поперечного сечения стержня А постоянна. К закреплённому концу стержня подводится тепловой поток q. На свободном конце стержня происходит конвективный теплообмен с окружающей средой. Распределение температуры в стержне описывается дифференциальным уравнением
Рассмотрим стержень длиной L с теплоизолированной боковой поверхностью, один из концов которого закреплён в стене. Площадь поперечного сечения стержня А постоянна. К закреплённому концу стержня подводится тепловой поток q. На свободном конце стержня происходит конвективный теплообмен с окружающей средой. Распределение температуры в стержне описывается дифференциальным уравнением