
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Линеаризация непрерывно дифференцируемых нелинейностейСодержание книги
Поиск на нашем сайте Выше было сказано, что линейное математическое описание систем и звеньев почти всегда является приближенным, поскольку характеристики элементов автоматики, как правило, нелинейные. Методы исследования нелинейных систем сложнее методов исследования линейных систем, поэтому, если это возможно, их стремятся линеаризовать. В этом разделе рассматривается наиболее распространенный метод линеаризации ¾ линеаризация непрерывно дифференцируемых (гладких) нелинейных характеристик. Идея метода заключается в замене исходной нелинейной характеристики Y = f(X) линейной в окрестностях некоторой точки с координатами X о, Y о (рис. 2.7.1). При этом линейная характеристика является касательной к исходной нелинейной в этой точке. Очевидно, что при малых отклонениях переменных от точки, в которой проведена такая замена, линейная характеристика довольно точно соответствует исходной нелинейной. Для упрощения линейной характеристики ее уравнение записывается в координатах с центром в точке замены. Тогда уравнение полученной линейной характеристики имеет вид: Y − Y о = K (X − X о ) или D Y = K D X. (2.7.7)
Рис. 2.7.1 Иллюстрация к вопросу линеаризации гладких нелинейных характеристик Теоретической основой такой линеаризации является разложение функции в ряд Тейлора в окрестностях точки с координатами X o, Y o:
Если ограничиться небольшой окрестностью точки разложения, то можно учитывать только линейные члены, а остальными пренебречь: Y(X) = Y(X o ) + Y1(X o )×(X − X o ).
Перенеся начало координат в точку с координатами X o, Y o и обозначив YI(X o ) = K, получим уравнение D Y = K D X.
В общем случае уравнение нелинейного звена имеет вид: f(X, XI, XII,...,Y, YI, YII,...) = 0. (*) Разложив эту функцию в ряд Тейлора в окрестностях точки с координатами X o, Y oи перенеся начало координат в точку разложения, получаем линеаризованное уравнение звена:
где все частные производные функции (*) вычисляются для точки с координатами X o, Y o. Разделим в полученном уравнении все члены на ¶ f/ ¶ Y. Обозначим коэффициенты при производных выходной величины Y как постоянные времени, коэффициенты при входном воздействии X и его производных как коэффициенты передачи. В результате получим линеаризованное уравнение звена. Обычно знак «D» приращения опускается, поскольку заранее известно, что линеаризованные уравнения записываются в отклонениях. Окончательно получаем линеаризованное уравнение и передаточную функцию звена общего вида:
Возможность исследования нелинейных систем путем исследования их линеаризованных математических моделей основана на следующем. Как правило, САР осуществляют процесс регулирования при сравнительно небольших отклонениях от требуемого установившегося режима. Например, системы стабилизации должны стабилизировать регулируемую величину. При этом все элементы системы также работают с небольшими отклонениями от своего установившегося режима, обусловленного заданным значением регулируемой величины. Если для рассматриваемого элемента системы установившийся режим соответствует точке (X о, Y о ), то линеаризацию следует проводить в этой точке. Линеаризация может быть проведена двумя методами: аналитическим и путем графоаналитической обработки полученной экспериментально нелинейной характеристики. При аналитической линеаризации уравнение исходной нелинейной характеристики дифференцируется по требуемой переменной. Коэффициенты находятся путем вычисления производных в точке линеаризации. При использовании второго метода экспериментально снимается статическая характеристика элемента. Коэффициент передачи находится как тангенс угла наклона касательной к нелинейной характеристике в точке линеаризации (К = D Y/ D Х). Графоаналитический метод применяется при линеаризации статических характеристик. В п. 2.6 было сказано, что если теоретическим путем математическое описание какого-либо объекта получить затруднительно или невозможно, то прибегают к идентификации этого объекта. Наиболее простой формой идентификации является идентификация линейных объектов по переходной функции.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-15; просмотров: 893; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.009 с.) |


 (2.7.8)
(2.7.8) ,
,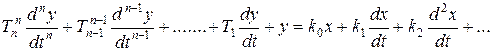 ; (2.7.9)
; (2.7.9) . …….. (2.7.10)
. …….. (2.7.10)


