
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Растяжение и сжатие стержней
Введение Методические указания к выполнению расчетно-графических заданий по курсу «Прикладная механика» для студентов немеханических специальностей всех форм обучения, учебным планом которых предусмотрено выполнение домашней работы в указанном курсе. Предлагаемые указания включают в себя рекомендации, задания и примеры, порядок расчета по выполнению расчетно-графических заданий. Изложены краткие теоретические сведения, необходимые для выполнения заданий. При выполнении расчетно-графических заданий по названному курсу студенты могут пользоваться программой расчета внутренних силовых факторов в поперечных сечениях стержня (при растяжении, изгибе), которая имеется на кафедре ОКМ и М, с целью развития и закрепления навыков программирования на ЭВМ. Предмет «Прикладная механика» содержит комплекс важнейших общетехнических знаний. Курс «Прикладная механика» для подготовки бакалавров и дипломированных специалистов немеханических специальностей состоит из разделов: 1) сопротивление материалов; 2) теория механизмов и машин; 3) детали машин. Назначение предмета – дать выпускникам немеханических специальностей сведения о методах и приемах постановки решения многих технических задач. Этим обусловлено важное значение прикладной механики как основы для изучения специальных дисциплин. Общие методические указания В соответствии с учебным планом студент при изучении курса «Прикладная механика» выполняет три расчетно-графических задания, которые соответствуют разделу программы курса «Сопротивление материалов» [1, 3]. После изучения материала, соответствующего каждому заданию, выполняется домашнее задание, в которое входят несколько задач, составленных по многовариантной системе. Студенты немеханических специальностей (ЭУП, ЭМ и т.д.) дневного и вечернего факультетов выполняют следующие расчетно-графические задания: задание № 1 – растяжение и сжатие; задание № 2 – кручение круглых стержней; задание № 3 – изгиб. Исходные данные к задачам, включенным в задание, студенты выбирают по индивидуальному варианту. Вариант – четырехзначное число, первая цифра которого – списочный номер студента в группе (в случае двухзначного числа – вторая его цифра), а следующие три назначаются преподавателем.
Пример. При варианте 2351 для задачи 1 необходимо взять из табл. 2.1 в соответствии с рис. 2.1 следующие данные: первая цифра – 2; F 1 = 2,7 кН; вторая цифра – 3; F 2 = 1,45 кН; третья цифра – 5; d 1 = 80 мм; четвертая цифра – 1; а 1 = 20 мм. Исходные данные в каждой задаче следует записать в виде табл.1.1. Например, таблица исходных данных к задаче 1 варианта 2351 будет иметь вид:
Таблица 1.1
Задачи, выполненные по данным, не соответствующим варианту студента, не принимаются.
Растяжение и сжатие стержней Нормальные напряжения и абсолютная Линейная деформация
Принимается, что во всех поперечных сечениях растянутых или сжатых стержней нормальные напряжения σ х распределены равномерно. Поэтому величина нормального напряжения σ х в произвольном поперечном сечении определяется отношением продольной силы Nx в этом сечении к его площади Ax:
Считая материалы стержней, подчиняющимися закону Гука, величину абсолютного удлинения стержня при растяжении или сжатии можно определить по следующей формуле [1]:
где Е – модуль упругости материала стержня, МПа. Интегрирование производится по длине каждого участка, а суммирование по всем участкам стержня. Если по длине
Варианты заданий
Задача 1 Стальной поршень пневмоцилиндра (рис. 2.3) находится в равновесии под действием рабочей нагрузки F 2, силы давления воздуха в цилиндре F 1 и силы пружины F 3. Найти продольные силы N, нормальные напряжения σ, перемещения
Рис. 2.3
Таблица 2.1
Задача 2 Для стального поршня пневмоцилиндра (рис.2.4) определить рабочую нагрузку F 3, продольные силы N, нормальные напряжения σ, перемещения

Рис. 2.4
Таблица 2.2
Задача 3 На стальном валу (рис. 2.5) находятся зубчатые колесами. На них действуют осевые силы F 1 и F 2, приведенные к оси вала. Определить продольные силы N, нормальные напряжения s, перемещения Ø d3 Ø
        а а 
Рис. 2.5
Таблица 2.3
Для бетонной опоры моста (рис. 2.6) определить продольные силы N, нормальные напряжения s, перемещения
1,5а

F2 F 1
A 2 A 1 Рис. 2.6
Таблица 2.4
3. Кручение стержня
Крутящий момент
Аналогично продольной силе при растяжении крутящий момент в поперечном сечении стержня определяется методом сечений. Величина крутящего момента Тк равна алгебраической сумме вращающих моментов всех внешних пар сил, действующих относительно геометрической оси стержня по одну сторону от рассматриваемого сечения. Общая формула, по которой можно определить величину крутящего момента в произвольном поперечном сечении на любом участке стержня, имеет вид [2]: Тk =∑ Ti (3.1) Суммирование производится по всем участкам, расположенным по одну сторону от рассматриваемого сечения. Крутящий момент, рассматриваемый со стороны внешней нормали к сечению, условно будем считать положительным, если он направлен против часовой стрелки, и наоборот.
Зависимость между вращающим моментом Т в Н∙м, угловой скоростью вращения ω 1/с и мощностью Р в Вт выражается формулой:
а между ω и числом оборотов в минуту n:
Поскольку вращающий момент пропорционален мощности, то для равномерно вращающихся валов, передающих мощности рабочим агрегатам, можно вместо эпюры крутящих моментов строить эпюру распределения моментов по длине вала [2]. Варианты заданий
Задача 1 Полый стальной вал (рис. 3.2) нагружен парами сил с моментами T 1, T 2, Т 3, Т 4, T 2= Т 3. Под действием момента Т 1 вал закручивается на угол j =0,2 радиана на длине а. Требуется определить диаметр вала, если даны в таблице 3.1: a=d/D, T 1, T 2, а. Построить эпюры крутящихся моментов Тк и углов закручивания j.

         
а а 0,5 а
Рис. 3.2
Таблица 3.1
Задача 2 На вал (рис. 3.3) насажаны три шкива. Первый шкив является ведущим и передает мощность N 1; N 2= N 3 (табл. 3.2). Частота вращения вала n, об/мин. Построить эпюры крутящих моментов Tk и углов закручивания j. Определить диаметр трубчатого сечения вала из условия прочности при a =d/D, если [τ]=80 MПа.
        Ø d Ø d
Рис. 3.3
Таблица 3.2
Задача 3 Ступенчатый стальной вал (рис. 3.4) нагружен парами сил с моментами Т 1, Т 2, Т 3 и Т 4 (табл. 3.3). Определить размеры вала, если [ tкр ] = 80 МПа. Построить эпюры крутящих моментов Tk и углов закручивания j. Определить, на какой угол закрутится последнее сечение относительно первого сечения.
Рис. 3.4 Таблица 3.3
Задача 4 Даны: N1 – мощность, подводимая к приводу (рис. 3.5); N 4= N 2; n – частота вращения вала (табл. 3.4); [t кр ]=30МПа – допускаемое напряжение кручения; [j] =0,4 град/м – допускаемый угол закручивания. Определить мощности N2 и N3, снимаемые с вала, и крутящие моменты Тk. Рассчитать диаметр сплошного вала. Построить эпюры Тk и j.
Ø d
a 2a a a a Рис. 3.5
Таблица 3.4
Прямой поперечный изгиб Нормальные напряжения
Балки рассчитывают на прочность по наибольшим нормальным напряжениям, возникающим в их поперечных сечениях. При поперечном изгибе балок наряду с нормальными возникают и касательные напряжения, обусловленные наличием поперечной силы, но они в подавляющем большинстве случаев невелики и при расчетах на прочность не учитываются. Прочность балки обеспечена, если наибольшие по абсолютному значению нормальные напряжения, возникающие в опасном сечении, не превышают допустимых. Для балки, поперечные размеры которой по всей длине постоянны, опасное сечение то, в котором возникает наибольший по модулю изгибающий момент.
где М max – наибольший изгибающий момент опасного сечения; W – осевой момент сопротивления данного поперечного сечения.
4.3. Построение эпюр Q и M
Пример. Балка на двух опорах, к которой приложены внешние нагрузки (рис. 4.3). Дано: F= 10 m, q = 2 m /м, a = 4 м. Построить эпюры Q и M. Решение. Определяем реакции опор из условия статического равновесия балки, т.е. суммы моментов сил относительно правой и левой опоры. Σ M (Fkx)B = 0; F ·3 a – R A·2 a + F · a – F · a + q ·3 a ·1,5· a - q + a2 ·0,5 = 0; 10·3·4 – R A· 2·4 + 10·4 + 2·4·4·0,5 = 0; R A =31 m; Σ M (Fkx)A = 0; - F ·3 + RB ·2 a – F · a – q ·3 a ·1,5 a + F · a + q · a 2·0,5 = 0; -10·3·4 – R B·2·4 – 10·4 – 2·3·4·1,5·4 + 10·4 + 2·42·0,5 = 0; R B = 31 m. Проверка: Σ F y = 0; 31+ 31 – 10 –10 –32 – 32 = 0. Для упрощения выражений, определяющих Q и M, сечения на первом и втором участках длиной a рассматриваем слева, а на третьем и четвертом участках – справа: 0≤ x 1≤ a; Q x1 = - F – qx 1; Q x1 = a = - F – q x1 – x1/2; M x1=0=0; M x1= a = - F · a – qa · a /2·-10·4·4/2 = -56 m ·м; M x1= a /2=-10·2 – 2·2·2/2 = -24 m ·м;
Х
X 1 X 2 X 3 X 4
a a a a
Рис. 4.3
0≤ х 2≤ a; M x2= - F (a + x 2) – qa (a /2 + x 2) + R A· x 2 – qx 2· x 2/2; M x2=0= -10·4 – 2·4·2 = -56 m ·м; M x2= a = -10·8 – 2·4·6 + 31·4 – 2·4·2 = -20 m ·м; M x2= a /2= -10·6 – 2·4·4 + 31·2 – 2·2·1 = -34 m ·м; Q x2=- F – q · a + R A – q · x 2; Q x2=0= -10 – 2·4 + 31 + 13 m; Q x2= -10 – 2·4 + 31 – 2·4 = 5 m ·м;
0≤ x 4≤ a; Q x4= F + qx 4; Q x4=0= F =10 m; Q x4= a = 10 + 2·4 =18 m; M x4= - F · x 4 – qx 4· x 4/2; M x4=0= 0; M x4= a = -10·4 – 2·4·2 = -56 m ·м; M x4= a /2= -10·2 – 2·2·1 = -24 m ·м;
0≤ x 3≤ a; Q x3= F + qa – R B + qx 3; Q x3=0= 10 + 2·4 – 31 = -13 m;
Q x3= a = 10 + 2·4 – 31 + 2·4 = 5 m ·м; M x3= - F (a + x 3) – qa ·(a /2 + x3) + RB · x 3 – qx 3· x 3/2; M x3=0= -10·4 – 2·4·2 = -56 m ·м; M x3= a = -10·8 – 2·4·6 + 31·4 – 2·4·2 = -20 m ·м; M x3= a /2= - 10·6 – 2·4·2 + 31·2 – 2·2·1 = -34 m ·м. По полученным данным построим эпюры Q и M (см. рис. 4.3).
Варианты заданий
Задача 1 Определить реакции опор балки (рис. 4.5), поперечные силы Q, изгибающие моменты M; построить эпюры Q и M, если известны нагрузки F, M0, q и d (табл. 4.1). Найти размеры поперечного сечения: стальной круглой балки при [σ]=160 МПа (схема a); стальной балки из профильного проката при [σ] =140МПа (схема б). Профиль – двутавр.
Q M 0
a A B
F q
б F M 0
2 d d d Рис. 4.5
Таблица 4.1
Задача 2 Определить реакции опор балки (рис. 4.6), поперечные силы Q, изгибающие моменты M и построить эпюры Q и M. Найти размеры поперечного сечения: стальной круглой балки при [σ] = 20 МПа (схема а); стальной балки из профильного проката при [σ] = 110 МПа (схема б). Профиль – швеллер. Известны нагрузки F, M 0, q и a (табл. 4.2). q M 0
а
q M 0
A B б F
a a a a
Рис. 4.6 Таблица 4.2
Задача 3
Определить реакции опор балки (рис. 4.7), поперечные силы Q, изгибающие моменты M и построить эпюры Q и M. Найти размеры поперечного сечения. Если известно, что для схемы а используется стальная труба [σ] = 120 МПа и α = d/D = 0,5, a для схемы б – деревянная прямоугольная балкя при [σ] = 9 МПа и в/h = 0,6. Известны н
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-15; просмотров: 404; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.14.148.63 (0.01 с.) |
 , (2.2)
, (2.2) (2.3)
(2.3) стрежня N и А постоянны в пределах участка нагружения, то абсолютное удлинение равно:
стрежня N и А постоянны в пределах участка нагружения, то абсолютное удлинение равно: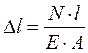 . (2.4)
. (2.4) и построить эпюры N,
и построить эпюры N, 


 а1 а2 а3
а1 а2 а3











 F1 d3 F2
F1 d3 F2
 Ø d 3
Ø d 3 Ø d 3
Ø d 3


 Ø d1 Ø d 4
Ø d1 Ø d 4


 F 2 F 1 F 3
F 2 F 1 F 3








 Ø d 2
Ø d 2





 а1 а2 а3 а4
а1 а2 а3 а4














 2а а 2 а 2 a 2 a a
2а а 2 а 2 a 2 a a










 2а а
2а а








 , (3.2)
, (3.2) (3.3)
(3.3)


















 Т 3
Т 3 



 Т 1
Т 1


 Т 2 a
Т 2 a
 ω
ω












 a 0,5a a
a 0,5a a
 N 1 N 2 N 3 N 4
N 1 N 2 N 3 N 4 , (4.1)
, (4.1) Y
Y
 F R A F R B F
F R A F R B F

 I II III IV
I II III IV






 A B
A B










 13 5 18 10
13 5 18 10 э Q, m
э Q, m

 -5
-5
 -10 -18 -13
-10 -18 -13




 э М z, m м
э М z, m м
 F
F


