
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Полевые методы испытания на сдвиг.Содержание книги
Поиск на нашем сайте
1. Основным способом определения предельного сопротивления сдвигу является метод крыльчатки – лопастные испытания на сдвиг при кручении впервые предложены в Швеции под названием «vane test». В настоящее время их широко применяют для испытания пластичных слабых глинистых и илистых грунтов, а также водонасыщенных супесчаных грунтов, пробы которых взять трудно, не нарушив их структуру. М Порядок проведения испытания: В забой скважины ниже конца обсадной трубы в грунт вдавливается лопастная крыльчатка (крестовина). После чего вращением рукоятки (с помощью двойного червячного редуктора) производится полный поворот (на 360º) и грунт срезается по цилиндрической поверхности, высотой h и диаметром d. При этом (торсиометром) замеряется максимальный скручивающий момент Мкр: Так как этот метод в основном используется для определения предельного сопротивления сдвигу слабых илистых и глинистых грунтов, принимается τs= C.
Полевые методы наиболее полно учитывают структурно – текстурные особенности грунта. Они не заменимы при исследовании торфов, глинисто – щебеночных или песчано – равелистых отложений, взятие образцов ненарушенной структуры которых невозможно.
Вопрос Напряжение в грунте от местной нагрузки рассеивается в пределах основания и с глубиной интенсивность его уменьшается. При известном вертикальном давлении, приложенном к поверхности какого-либо слоя грунта, осадку можно определить по формуле В основу метода послойного суммирования положены следующие допущения: 1. Грунт в основании представляет собой сплошное, изотропное, линейно-деформированное тело; 2. Осадка обусловлена действием только напряжения 3. Боковое расширение грунта в основании невозможно; 4. Напряжение 5. При определении напряжения 6. Фундаменты не обладают жёсткостью; 7. Деформации рассматриваются только в пределах сжимаемой толщи мощностью 8. Значение коэффициента Достоинством метода послойного суммирования является его универсальность и ясность оценки работы грунта основания. Распределение напряжений в массиве грунта от сосредоточенной силы. Напряжение – это средняя величина непрерывно распределенных в сечении внутренних сил, приходящихся на единицу площади сечения. При горизонтальной поверхности и отсутствии бокового расширения грунта для определения компонентов напряжений от его собственного веса используются зависимости
При однородной толще грунтов
При слоистой
где ξ – коэффициент бокового давления;
Если закон распределения давления по поверхности изотропного линейно-деформируемого полупространства известен, то элементарное суммирование можно заменить интегрированием. При равномерно распределенном давлении после интегрирования по прямоугольной площади загружения значения σz для точек, расположенных под центром прямоугольной площади загружения будут
Где а — коэффициент, принимаемый по табл.; р — равномерно распределенное давление. При определении напряжения сгг на глубине z под центром площади загружения значение а принимают в зависимости от величин η=l/b и ξ=2z/b (где l— длинная сторона прямоугольной площади загружения; b— ее ширина). При нахождении σz под угловыми точками прямоугольной площади загружения в зависимости от величин η=l/b и ξ. В этом случае ξ=z/b. Напряжение под угловыми точками определяют по формуле
Вопрос Метод угловых точек позволяют определить сжимающие напряжения в основании по вертикали, проходящей через любую точку поверхности. Возможны три варианта решения Пусть вертикаль проходит через точку Если точка Наконец, если точка
Вопрос
|
||||||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 778; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.40.234 (0.006 с.) |

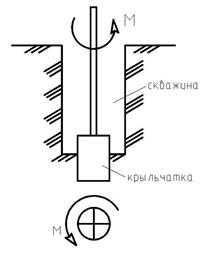 етод крыльчатки
етод крыльчатки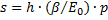 . Вследствие постепенного изменения напряжений по глубине основания его толщу можно разбить на ряд слоёв и в каждом из них определить напряжение. Это и принято в методе послойного суммирования.
. Вследствие постепенного изменения напряжений по глубине основания его толщу можно разбить на ряд слоёв и в каждом из них определить напряжение. Это и принято в методе послойного суммирования.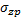 , остальные пять компонентов напряжений не учитываются;
, остальные пять компонентов напряжений не учитываются;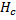 ;
;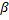 принимается равным 0,8 независимо от характера грунта.
принимается равным 0,8 независимо от характера грунта.
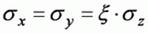


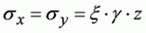





 , лежащую на контуре прямоугольника. Разделив этот прямоугольник на два так, чтобы точка М являлась угловой для каждого из них, можно представить напряжения
, лежащую на контуре прямоугольника. Разделив этот прямоугольник на два так, чтобы точка М являлась угловой для каждого из них, можно представить напряжения  как сумму угловых напряжений I и II прямоугольников, т.е.
как сумму угловых напряжений I и II прямоугольников, т.е.


