
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Класс двунаправленного списка.Содержание книги Поиск на нашем сайте
Имеется набор связанных между собой узлов. Помимо ссылки на след. узел, есть ссылка на предыдущий. Двунаправленные списки позволяют осуществить движение в обоих направлениях по цепи. Деревья представляют собой более сложные структуры, в которых один узел может содержать ссылки на два или три следующих узла. #include "iostream.h" class list { private: int data; list * prev; list * next; public: static list * first; static list * current; static void ins(int a); static int del(); static void clear();}; list * list::first=NULL; list * list::current=NULL; //вставка после текущего элемента void list::ins(int a) { list * newnode; newnode=new list; newnode->data=a; if(current!=NULL) { newnode->next=current->next; current->next=newnode; } Else newnode->next=NULL; newnode->prev=current; if(newnode->next!=NULL) newnode->next-> prev=newnode; current=newnode; if(first==NULL)first=current;} int list::del() { list * prevnode; int result; if(current==NULL)return -1; result=current->data; prevnode=current->prev; if(prevnode!=NULL) prevnode->next=current->next; if(current->next!=NULL) current->next-> prev=prevnode; if(current==first)first=current->next; delete current; current=prevnode; if((current==NULL)&&(first!=NULL))current=first; return result;} void list::clear() { while(first!=NULL)del(); } void main() { list l; l.ins(1); l.ins(2); l.ins(3); cout<<l.del()<<endl; l.current=l.first; cout<<l.del()<<endl; cout<<l.del()<<endl; cout<<l.del()<<endl; } Алгоритм поиска. Хеширование. Класс хеш-таблицы. Линейный поиск Большинство задач поиска сводится к простейшей — к поиску в массиве элемента с заданным значением. Рассмотрим именно эту задачу. Пусть требуется найти элемент Х в массиве А. В данном случае известно только значение разыскиваемого элемента, никакой дополнительной информации о нем или о массиве, в котором производится поиск, нет. Наверное, единственным способом является последовательный просмотр массива и сравнение значения очередного рассматриваемого элемента массива с X. Напишем фрагмент: for(int i=0;i<=n;i++) if (a[i]=X) k=i; А если исключить лишние проверки? Совпадение найдено, зачем делать "пустую" работу? for(int i=0;i<=n;i++) if (a[i]=X) { k=i; i=n; } Очевидно, что число сравнений зависит от местонахождения искомого элемента. В среднем количество сравнений равно (N + 1) div 2, в худшем случае, когда элемента нет в массиве, N сравнений. Эффективность поиска — O(N). Бинарный поиск Если никаких дополнительных сведений о массиве, в котором хранятся данные, нет, то ускорить поиск нельзя. Если же заранее известна некоторая информация о данных, среди которых ведется поиск, например, известно, что массив данных отсортирован, то удается сократить время поиска, используя бинарный (двоичный, дихотомический, методом деления пополам — все это другие названия алгоритма, основанного на той же идее) поиск. Итак, требуется определить место Х в отсортированном массиве А. Идея бинарного метода - делим пополам и сравниваем Х с элементом, который находится на границе этих половин. Отсортированность А позволяет по результату сравнения со средним элементом массива исключить из рассмотрения одну из половин. Программная реализация бинарного поиска может иметь следующий вид. void search(int x) {int i,j,m; bool f; i=0; j=N;//На 1-ом шаге рассматривается весь массив. f=false; //Признак того, что x не найден. while ((i<=j) && (!f) {m = (i+j) / 2; if (A[m]=x) f=true //Элемент найден, поиск прекращается. else if A[m]<x i:=m+l //Исключаем из рассмотрения левую часть А. else j:=m-l {Правую часть.}}} Предложим еще одну, рекурсивную, реализацию изучаемого поиска. Int Search (int i,j) { //Массив А и переменная Х глобальные величины int m; If (i>j) return -1else {m=(i+j)/2; If A[m]>X Search(i,m-l) Else return m;}} Хеширование Выше описанные 2 метода основаны на сравнении данного аргумента К с ключами в таблице или на использовании его цифр для управления процессом разветвления. Третий путь – отказаться от поиска по данным и выполнить арифметические действия над К, позволяющие вычислить некоторую функцию f(K). Последняя укажет адрес в таблице, где хранится К и связанная с ним информация. Недостаток – нужно заранее знать содержимое таблицы.. Добавив всего одно значение может придется начать работу с нуля. Может случится что найдутся различные ключи Ki<>Kj имеющие одинаковые значение хеш-функций f(Ki)<>f(Kj). Такое событие называется коллизией. Для использования хеширования программист должен решить 2 практические задачи – выбрать хеш- Параметризированная функция бинарного поиска в массиве. #include <iostream.h> template <class Stype> int binary_search(Stype *item, int count, Stype key); int main () {char str[]="acdefg"; int nums[] = { 1, 5, 6, 7, 13, 15, 21 }; int index; index = binary_search(str, (int)sizeof(str), 'd'); if (index>=0) cout << "Найдено совпадение в позиции: " << index << endl; else cout << "Совпадение не найдено\n"; index = binary_search(nums, 7, 21); if (index>=0) cout << "Найдено совпадение в позиции: " << index << endl; else cout << "Совпадение не найдено\n"; return 0;} template <class Stype> int binary_search(Stype *item, int count, Stype key) {int low=0, high = count-1, mid; while (low<= high) {mid = (low + high) /2; if (key < item[mid]) high = mid - 1; else if (key>item[mid]) low = mid+1; else return mid; // совпадение} return -1;} Кодування символів, алгоритм Хаффмана. Идея, лежащая в основе кода Хаффмана, достаточно проста. Вместо того чтобы кодировать все символы одинаковым числом бит, будем кодировать символы, которые встречаются чаще, меньшим числом бит, чем те, которые встречаются реже. Первым такой алгоритм опубликовал Д. Хаффман в 1952 году. Алгоритм Хаффмана двухпроходный. На 1-ом проходе строится частотный словарь и генерируются коды. На 2-ом проходе происходит непосредственно кодирование. Стоит отметить, что за более чем 50 лет со дня опубликования, код Хаффмана ничуть не потерял своей актуальности и значимости. Так с уверенностью можно сказать, что мы сталкиваемся с ним, в той или иной форме (дело в том, что код Хаффмана редко используется отдельно, чаще работая в связке с другими алгоритмами), практически каждый раз, когда архивируем файлы, смотрим фотографии или слушаем музыку. Код Хаффмана Определение 1. Пусть A={a1,a2,...,an} - алфавит из n различных символов, W={w1,w2,...,wn} - соответствующий ему набор положительных целых весов (например, частот появления этих символов). Тогда набор бинарных кодов C={c1,c2,...,cn}, такой что: (1) ci не является префиксом для cj, при i!=j (2) называется минимально-избыточным префиксным кодом или иначе кодом Хаффмана. Замечания: Свойство (1) называется свойством префиксности. Оно позволяет однозначно декодировать коды переменной длины. Сумму в свойстве (2) можно трактовать как размер закодированных данных в битах. На практике это очень удобно, т.к. позволяет оценить степень сжатия не прибегая непосредственно к кодированию. В дальнейшем, чтобы избежать недоразумений, под кодом будем понимать битовую строку определенной длины, а под минимально-избыточным кодом или кодом Хаффмана - множество кодов (битовых строк), соответствующих определенным символам и обладающих определенными свойствами. Известно, что любому бинарному префиксному коду соответствует определенное бинарное дерево. Опреде 2. Бинарное дерево, соответствующее коду Хаффмана, будем называть деревом Хаффмана. Задача построения кода Хаффмана равносильна задаче построения соответствующего ему дерева. Приведем алгоритм построения дерева Хаффмана: Составим список кодируемых символов (при этом будем рассматривать каждый символ как одноэлементное бинарное дерево, вес которого равен весу символа). Из списка выберем 2 узла с наименьшим весом. Сформируем новый узел и присоединим к нему, в качестве дочерних, два узла выбранных из списка. При этом вес сформированного узла положим равным сумме весов дочерних узлов. Добавим сформированный узел к списку, а два выбранных узла исключим из списка. Если в списке больше одного узла, то повторим пункты 2-5.
Рис. 13. Дерево Хаффмана для фразы ‘abrakadabra’. Таким образом, дерево Хаффмана строится снизу вверх - от "листьев" к корню. Символы, которые встречаются чаще, находятся ближе к корню дерева и получают более короткие коды. Коды символов вычисляются следующим образом: начинаем от корня дерева; добавляем '0', каждый раз, когда переходим к левому "потомку" узла, '1' - к правому потомку.
Расжатие потока происходит очень просто: начинаем с корня дерева; берём левого потомка, каждый раз, когда в потоке появляется бит '0', и правого потомка, когда в потоке появляется бит '1'. При достижении конечного узла дерева, выводим символ в выходной поток и переходим к корню дерева. И так до тех пор, пока входой поток бит не закончится. Одним из самых существенных недостатков данного алгоритма является необходимость дважды проходить по потоку данных: один раз для подсчёта таблицы вероятностей символов и построения дерева, второй раз для непосредственной кодировки.
функцию и способ разрешения коллизий (методом цепочек, открытой адресации, деления). Рассм простую задачу. Количество различных буквосочетаний длиной не более 4 символов из 32 букв русского алфавита чуть больше 10^6. При линейном поиске в худшем случае для ответа на вопрос "есть или нет" потребуется 10^6 сравнений, при бинарном — порядка 50. Можно ли уменьшить количество сравнений и уменьшить объем требуемой оперативной памяти, резервировать не 10^6, а, например, 10^3 элементов памяти? Обозначим цифровой аналог буквосочетания символом R, а адрес в массиве через А. Если будет найдено преобразование f(R), дающее значение А такое, что f выполняется достаточно быстро; случаев, когда f(R1) = f(R2), будет минимальное количество, то задача поиска трактуется совсем иначе, чем рассмотрено выше. Этот способ поиска называется хешированием. Итак, ключ преобразуется в адрес, в этом суть метода. Хеш-функция Для определенности полагается, что хеш-функция имеет не более М различных значений, при чем для всех К 0<=h(K)<M. На практике ключи зачастую избыточны, поэтому нужно внимательно выбирать хеш-функцию. Многочисленные тесты показали хорошую работу двух основных типов хеш-функций(один основан на делении, второй на умножении). Метод деления h(K) = K mod M. Метод умножения h(k)=M A/w K. W – размер машинного слова. А – некоторое целое число. Хорошая хеш-функция должна удовлетворять 2 требованиям: 1. ее вычисление должно выполняться очень быстро 2. она должна минимизировать количество коллизий. Хеш-таблица
Самая простая структура описывающая хеш-таблицу: struct list{int el;list *next;}; list hashtable[n];
|
||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-14; просмотров: 177; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.202.60 (0.007 с.) |

 минимальна (
минимальна (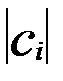 - длина кода ci)
- длина кода ci) Рассмотрим процесс построения дерева Хаффмана на примере фразы "abrakadabra". Первым шагом, необходимо построить таблицу частот символов, в которой отображено количество каждого символа в данном сообщении. В нашем случае она будет иметь вид: a - 5, b - 2, r - 2, d - 1, k - 1. Далее, следуем описанному выше алгоритму. Полученное дерево показано на рис. 13.
Рассмотрим процесс построения дерева Хаффмана на примере фразы "abrakadabra". Первым шагом, необходимо построить таблицу частот символов, в которой отображено количество каждого символа в данном сообщении. В нашем случае она будет иметь вид: a - 5, b - 2, r - 2, d - 1, k - 1. Далее, следуем описанному выше алгоритму. Полученное дерево показано на рис. 13.



