
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Із чисел 2; 4; 6; 8; 10 навмання вибрали одне. Яка ймовірність того, що ним виявиться число 4.
А) 1.7. Яка з нерівностей є правильною при будь-яких значеннях х? А) х2 + 10 < 0; Б) (x-5)2 1.8. Знайдіть кут при вершині рівнобедреного трикутника, якщо кут при основі дорівнює 30◦. А) 60◦; Б) 120◦; В) 40◦; Г) 90◦. Катети прямокутного трикутника дорівнюють 6см і 8см. Знайдіть тангенс протилежного кута до більшого з катетів. А) 1.10. Знайдіть відстань від точки А (-8; 6) до початку координат. А) Частина друга Розв’яжіть завдання 2.1 – 2.4 і запишіть відповідь. 2.1. При яких значеннях х сума дробів Задайте формулою функцію яка є прямою пропорційністю, якщо її графік проходить через точку А(-2; 3). 2.3. Знайдіть суму нескінченної геометричної прогресії bn, якщо b3 = 6, b4 = -3. 2.4. Сторона трикутника дорівнює 12см, а радіус описаного кола 4 Частина третя Розв’язання завдань 3.1-3.3 повинні мати обґрунтування. У них потрібно записати послідовні логічні дії та пояснення, зробити посилання на математичні факти, з яких випливає те чи інше твердження. Якщо потрібно, проілюструйте розв’язання схемами, графіками, таблицями. 3.1. Рибалка відправився на човні з пункту А проти течії річки. Пропливши 3 км, він кинув весла, і через 4 год 30 хв після відправлення з пункту А течія його віднесла до цього пункту. Знайдіть швидкість течії, якщо швидкість човна у стоячій воді дорівнює 2,7 км/год. 3.2. Розв’яжіть рівняння (х2 + х – 3) (х2 + х – 1) = 3. 3.3. Сторони трикутника дорівнюють ВАРІАНТ 7 Частина перша Завдання 1.1-1.10 мають по чотири варіанти відповіді, в яких тільки ОДНА відповідь ПРАВИЛЬНА. Оберіть правильну, на Вашу думку, відповідь і запишіть її. 1.1. Розв’яжіть рівняння х: 65 = 910. А) 5915; Б) 59150; В) 14; Г) 131. 1.2. Обчисліть 5 А) 50 1.3. Подайте у вигляді многочлена вираз (3а -b)2. А) 9а2 - b2; Б) 9а2 – 6 аb + b2; В) 9а2 – 3а b + b2 ; Г) 9а2 + 6 аb + b2. 1.4. Розкладіть на множники вираз 3m + mk - 3n – kn. А) (3 + k)(m – n); Б) m(3 + k) - n(3- k); В) (m + n) (3 - k); Г) (m – n) (3 - k); 1.5. Обчисліть значення виразу 80 ∙ 2-3 – 22. А) 40; Б) 636; В) 14; Г) 6. 1.6. Виконайте ділення
А) Розв’язком якої з нерівностей є число -2? А) –х2- 2х + 3 < 0; Б) х2- 6х + 8 < 0;
1.8. Якою має бути градусна міра кута х, щоб прямі с і d були паралельними (див.рис.)? А) 15◦; Б) 150◦; В) 105◦; Г) 75◦. 1.9. Знайдіть довжину дуги кола, градусна міра якої дорівнює 60 ◦, якщо радіус кола 3 см. А) 1.10. Площа гострокутного трикутника АВС дорівнює 20 А) 30◦; Б) 45◦; В) 90◦; Г)60◦. Частина друга Розв’яжіть завдання 2.1 – 2.4 і запишіть відповідь. 2.1. Розв’яжіть рівняння 3 2.2. При яких значеннях а і нулями функції у = ах2+ 8х + с є числа -6 і 2? У наметі знаходяться шість туристів, середній вік яких становить 23 роки. Після того як з намету вийшов один турист, середній вік тих, хто залишився, став 24 роки. Скільки років туристу, який вийшов з намету? 2.4. Знайдіть площу круга, вписаного у квадрат, площа якого дорівнює 12 см2. Частина третя Розв’язання завдань 3.1-3.3 повинні мати обґрунтування. У них потрібно записати послідовні логічні дії та пояснення, зробити посилання на математичні факти, з яких випливає те чи інше твердження. Якщо потрібно, проілюструйте розв’язання схемами, графіками, таблицями. 3.1. Потяг мав проїхати 300 км. Проїхавши 3.2. Знайдіть цілі розв’язки системи нерівностей ВАРІАНТ 8 Частина перша Завдання 1.1-1.10 мають по чотири варіанти відповіді, в яких тільки ОДНА відповідь ПРАВИЛЬНА. Оберіть правильну, на Вашу думку, відповідь і запишіть її. 1.1. Знайдіть суму А) 37 см; Б) 35 1.2. Знайдіть різницю А) 1.3. Спростіть вираз 7х – (2а - х). А ) 6х – 2а; Б) 8х – 2а; В) 6х + 2а; Г) 6ха. 1.4. Знайдіть точку перетину графіка функції у = 5х – 20 з віссю абсцис. А) (0; 4); Б) (0; -20); В) (4; 0); Г) (-4; 0). 1.5. Виконайте множення А) 6х8у4; Б)
1.6. Обчисліть значення виразу А) 7 +
А) -1; Б) -2; В) -3; Г) 0. 1.8. Бісектриса кута А утворює його стороною кут 25 ◦. Знайдіть градусну міру кута, суміжного з кутом А. А) 25◦; Б) 50◦; В) 130◦; Г) 75◦. 1.9. Кути рівнобічної трапеції можуть дорівнювати … А) 150◦ і 120◦; Б) 40◦ і 50◦; В) 155◦ і 35◦; Г) 70◦ і 110◦. Складіть рівняння кола з центром у точці М(-3; 1), що проходить через точку К(-1; 5). А) (х + 1)2 + (у - 5)2 = 20; Б) (х + 3)2 + (у - 1)2 = 20; В) (х + 3)2 + (у - 1)2 = 52; Г) (х + 1)2 + (у - 5)2 = 52. Частина друга
|
||||||
|
Последнее изменение этой страницы: 2016-07-11; просмотров: 345; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.146.178.220 (0.009 с.) |
 ; Б)
; Б)  ; В)1; Г)
; В)1; Г)  .
. 0; B) (x-1)2 > 0; Г) –x2 + 10
0; B) (x-1)2 > 0; Г) –x2 + 10  0.
0. ; Б)
; Б)  ; Г)
; Г)  .
. ; Б)
; Б)  ; В)9; Г) 10.
; В)9; Г) 10. і
і 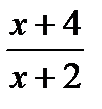 дорівнює 1?
дорівнює 1?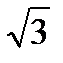 см. Чому дорівнює градусна міра кута трикутника, протилежного до даної сторони?
см. Чому дорівнює градусна міра кута трикутника, протилежного до даної сторони? см і 2 см. Знайдіть третю сторону трикутника, якщо вона дорівнює радіусу кола, описаного навколо цього трикутника.
см і 2 см. Знайдіть третю сторону трикутника, якщо вона дорівнює радіусу кола, описаного навколо цього трикутника. ∙ 10.
∙ 10. Б) 50; В) 14; Г) 56.
Б) 50; В) 14; Г) 56.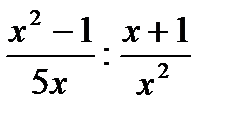 .
. ; Б)
; Б)  ; В)
; В)  ; Г)
; Г)  .
. В) 2х2- 3х + 1 > 0; Г) х2+ 5х - 7 > 0.
В) 2х2- 3х + 1 > 0; Г) х2+ 5х - 7 > 0. см; Б) 2
см; Б) 2 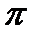 см; В)
см; В) 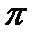 см; Г)
см; Г)  см.
см. см2. Знайдіть градусну міру В трикутника, якщо АВ= 8см, ВС = 10см.
см2. Знайдіть градусну міру В трикутника, якщо АВ= 8см, ВС = 10см. - 6 =0.
- 6 =0. шляху, він зупинився на 1 год, а потім продовжив рух із швидкістю на 10 км/год меншою за початкову. Знайдіть швидкість потяга до зупинки, якщо в пункт призначення він прибув через 8 год після виїзду.
шляху, він зупинився на 1 год, а потім продовжив рух із швидкістю на 10 км/год меншою за початкову. Знайдіть швидкість потяга до зупинки, якщо в пункт призначення він прибув через 8 год після виїзду. 3.3. У ромбі висота, що проведена з вершини тупого кута, ділить сторону навпіл. Знайдіть площу ромба, якщо його більша діагональ дорівнює 4
3.3. У ромбі висота, що проведена з вершини тупого кута, ділить сторону навпіл. Знайдіть площу ромба, якщо його більша діагональ дорівнює 4  см.
см. м + 35 см у сантиметрах.
м + 35 см у сантиметрах. .
. ; Б)
; Б)  ; В)
; В)  ; Г
; Г  .
. .
. ; В) 6х3у3; Г)
; В) 6х3у3; Г) 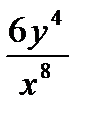 .
.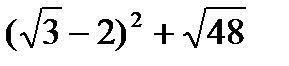 .
.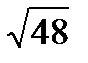 ; Б) -1 +
; Б) -1 +  ; В) 7; Г) -1.
; В) 7; Г) -1. 1.7. На рисунку зображено графік функції у = х2 + 4х + 3. Укажіть найменше значення функції.
1.7. На рисунку зображено графік функції у = х2 + 4х + 3. Укажіть найменше значення функції.


