Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Исследование шарнирно-рычажного шестизвенного механизмаСодержание книги
Поиск на нашем сайте
Исходные данные LOA=0.25м; LAB=1.0м; LBE=0.15м; LEC=1.1м
Построение кинематической схемы и структурный анализ механизма Определение скоростей Величина скорости точки А определяется по формуле VА = ω1⋅ lОА, м/с, где lОА = KL ⋅ ОА – длина кривошипа, м; ОА – отрезок на чертеже, изображающий в масштабе KL длину кривошипа, мм; а направление – в соответствии с направлением ω1 (перпендикулярно ОА). Для определения скорости точки В составим векторное уравнение:
В этом уравнении известны величина и направление вектора В этом уравнении два неизвестных элемента: величина скорости VB и VBA. А так как векторное уравнение соответствует двум скалярным, то указанное уравнение имеет определенное решение. Для определения этих неизвестных строим многоугольник (план) скоростей. По указанному в задании отрезку оа, изображающему на чертеже скорость VA, подсчитываем масштаб скорости: KV = VA/oa, м/(с⋅мм) (оа =70 мм). Из произвольно взятой на чертеже точки "о" откладываем отрезок оа перпендикулярно ОА. Через конец этого отрезка (точку а) проводим прямую перпендикулярно АВ, а через точку "о" – прямую, параллельную OY. Полученная от пересечения этих прямых точка b определяет длины отрезков оb и аb, которые изображают на чертеже скорости VB и VBA. Величины этих скоростей: VB = ob⋅KV, м/с; VBA = ab⋅KV, м/с. Для определения скорости точки C составим два уравнения: и решим их совместно. Для чего через точку a проведем прямую перпендикулярно AD и через точку b – прямую перпендикулярно DB.
Пересечение этих прямых определяет точку d, отрезок od и, следовательно, скорость VD, численное значение которой VD = od⋅KV, м/с. Для определения скорости точки C составим векторное уравнение:
В этом уравнении известны величина и направление вектора В этом уравнении два неизвестных элемента: величина скорости VC и VCD. Из точки "d" проводим прямую перпендикулярно СD, а через точку "о" – прямую, перпендикулярную OC. Полученная от пересечения этих прямых точка" c" определяет длины отрезков ос и cd, которые изображают на чертеже скорости VC и VCD. Величины этих скоростей: VC = oc⋅KV, м/с; VCD = cd⋅KV, м/с.
Скорость точки S4 определяется так: центр тяжести звена 4 находится на середине отрезка DC, из этого мы можем найти положение точки S4 на плане скоростей, она будет находиться на середине отрезка ds. Соединяем точку о и, найденную точку s4, таким образом получаем искомую скорость точки S4. Величина этой скорости: VS4 = os4⋅KV, м/с; Для определения положения точки S2 на плане скоростей составим пропорцию:
Таким образом нашли положение точки sII на плане скоростей. Значение скорости точки sII равно: VS2 = os2⋅KV, м/с. Теперь найдем угловые скорости звеньев.Угловая скорость шатуна 2: ω2 = VBA / lAB, 1/c, где lAB = KL⋅ AB – длина шатуна 1м; Угловая скорость шатуна 4:
где lCD = KL⋅ СD – длина шатуна 1.1м; На примере 9-го положения: VA=w1*LOA =35*0,25=8,75 (м/с) Kv=VA/oa=8,75/70=0,125 (м/(с*мм)) VB=VA+VB VB=ob*Kv =27,36*0,125=3,42 (м/с) VBA=ab*Kv=61,1*0,125=7,64 (м/с) VD=od*Kv=29,92*0,125=3,74 (м/с) VDA=ad*Kv=51,94*0,125=6,5 (м/с) VC=oc*Kv=34,68*0,125=4,335 (м/с) VCD=cd*Kv=5,79*0,125=0,74 (м/с) VS4=os4*KV=32,26*0,125=4,04 (м/с) VS4D=ds4*KV=9.96*0,0714=0,711 (м/с) VS2 = os2⋅KV=38,9*0,125=4.83 (м/с) VS2A = as2⋅KV=36,66*0,125=4,58 (м/с) ω2=VBA/LAB=2.56 /1=2.56 (1/c ) ω4=VCD/LCD=0,73 /1.1=0,66 (1/c ) ω5=VC/LOC=4,335 /0.7=6,2 (1/c ) Результаты расчета скоростей для 12-ти положений приведены в (Табл.1). Таблица 1 Результаты расчета скоростей:
Определение ускорений Перейдем теперь к определению ускорений. Ускорение точки А определяется по формуле
(так как ω1=const и ε1=0) и направлено от точки А к точке О. Ускорение точки B находится из уравнения
где В этом уравнении , м/с2 Для решения уравнения из произвольно взятой точки "о" проводим вектор
с его конца строим вектор
Длины отрезков соответствующие ускорениям
где Kа – произвольно взятый масштаб ускорения, м/(с2*мм)
В полученной точке пересечения прямых будет точка "b". Где будут концы векторов изображающие скорости Численное значение этих ускорений
Угловое ускорение 2 звена находится по формуле
Для установления направления ε2 и перенесем ускорения Ускорение точки D находим из уравнений:
где Значение ускорений
Длины отрезков соответствующие ускорениям
Для решения уравнения из точки "о" проводим вектор
Для определения ускорения точки C, принадлежащей звену 4 составим уравнение, так как точка С принадлежит звену 4 и 5, то уравнение выглядит следующим образом
где
где Значение ускорений
Длины отрезков, соответствующие ускорениям
Окончательный вид уравнения будет следующим:
В этом уравнение неизвестны лишь значения двух ускорений Для их нахоңдения решаем уравнение графическим способом. Из точки "а" проводим отрезок Численное значение
Угловое ускорение 4 и (условно)5 звеньев находятся по формуле:
Ускорение точки центра масс второго и четвертого звеньев находятся по следующим формулам
Все части уравнения уже известны.
Длины отрезков, соответствующие ускорениям
Из точки "а" проводим отрезок
Из точки "е" проводим отрезок
Результаты расчета ускорений для 2 и 6 положения приведены в (Табл.2). Таблица 2 Результаты расчета ускорений
Силовой анализ механизма Для силового анализа необходимо следующее: кинематическое исследование (определение скоростей и ускорений характерных точек механизма, включая центров масс звеньев, а также угловых скоростей и угловых ускорений звеньев) которого должно быть проведено заранее. Известны массы (mi) и моменты инерции (Ii) * звеньев. Требуется определить силы, приложенные к звеньям. Силами трения пренебрегаем. При отсутствии сил трения сила, с которой одно звено действует на другое, всегда направлена по нормали к поверхности их касания. Так, для вращательной пары эта сила проходит через центр вращательной пары (центр шарнира), для поступательной – перпендикулярно направляющей поступательной пары. При силовом исследовании механизм расчленяется на звенья (группы звеньев) и силовой расчет начинается с последнего звена, а заканчивается входным звеном (кривошипом 1), т. е. обратно порядку кинематического исследования.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-06-24; просмотров: 233; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.59.182.74 (0.011 с.) |

 1=35 рад/с
1=35 рад/с
 , а также направления векторов
, а также направления векторов  (|| OY) и
(|| OY) и 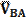 (⊥ АВ).
(⊥ АВ).

 , а также направления векторов
, а также направления векторов  (⊥OC) и
(⊥OC) и 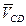 (⊥ CD).
(⊥ CD).
 1/c,
1/c, , м/с2,
, м/с2,
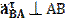

 получено выше, а
получено выше, а  находится по формуле
находится по формуле ,
, , а с его конца строим прямую перпендикулярную к АВ, а точки "о" проводим прямую параллельную OY
, а с его конца строим прямую перпендикулярную к АВ, а точки "о" проводим прямую параллельную OY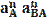 находят по следующей формуле
находят по следующей формуле , мм
, мм , мм
, мм
 и
и  .
.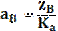

 , 1/c2
, 1/c2 в точку В и, рассматривая движение В относительно точек А, установим, что ε2 направлено против часовой стрелки.
в точку В и, рассматривая движение В относительно точек А, установим, что ε2 направлено против часовой стрелки.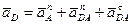
 Õ∥АВ,
Õ∥АВ,  ⏊ АВ
⏊ АВ
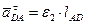

 , начало которого в точке "о", а конец в точке "d".
, начало которого в точке "о", а конец в точке "d".


 складывается из нормального
складывается из нормального 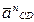 и тангенсального ускорения
и тангенсального ускорения  т.е.
т.е.
 также двигается по своей окружности и, поэтому ускорения так же будет иметь нормальную и тангенсальную составляющую
также двигается по своей окружности и, поэтому ускорения так же будет иметь нормальную и тангенсальную составляющую


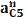 находятся по формулам:
находятся по формулам: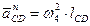 , м/с2
, м/с2 , м/с2
, м/с2
 , находятся по следующим формулам:
, находятся по следующим формулам:

 и
и  .
.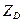 , равный
, равный  , мм., на его конце будет точка "d". Из точки "d" откладываем отрезок
, мм., на его конце будет точка "d". Из точки "d" откладываем отрезок 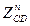 , с его конца проводим прямую перпендикулярную CD. Далее из точки "о" проводим отрезок
, с его конца проводим прямую перпендикулярную CD. Далее из точки "о" проводим отрезок  на его конце проводим прямую перпендикулярную OC. В точке пересечения прямых получим точку С. Полученные отрезки будут соответствовать длинам ускорений
на его конце проводим прямую перпендикулярную OC. В точке пересечения прямых получим точку С. Полученные отрезки будут соответствовать длинам ускорений 
 будет равно
будет равно , м/с2
, м/с2 , м/с2
, м/с2
 , 1/c2
, 1/c2

 , м/с2
, м/с2 , м/с2
, м/с2
 , м/с2
, м/с2 , м/с2
, м/с2
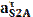

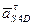 находятся по следующим формулам
находятся по следующим формулам , мм
, мм , мм
, мм , мм
, мм , мм
, мм , а с его конца отрезок
, а с его конца отрезок  . На конце последнего отрезка будет находится точка s2. Отрезок os2 будет соответствовать вектору ускорения
. На конце последнего отрезка будет находится точка s2. Отрезок os2 будет соответствовать вектору ускорения  . Его численное значение будет равно
. Его численное значение будет равно , м/с2
, м/с2 , а с его конца отрезок
, а с его конца отрезок  . На конце последнего отрезка будет находится точка s4. Отрезок os4 будет соответствовать вектору ускорения
. На конце последнего отрезка будет находится точка s4. Отрезок os4 будет соответствовать вектору ускорения  . Его численное значение будет равно
. Его численное значение будет равно , м/с2
, м/с2