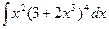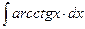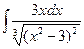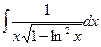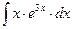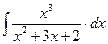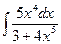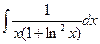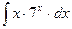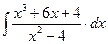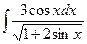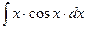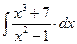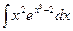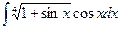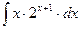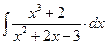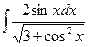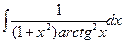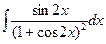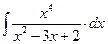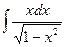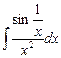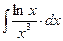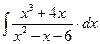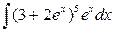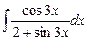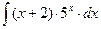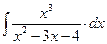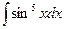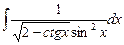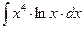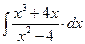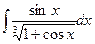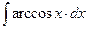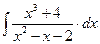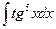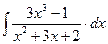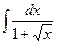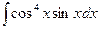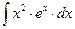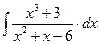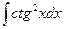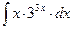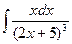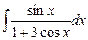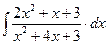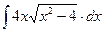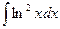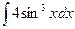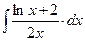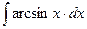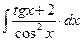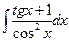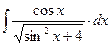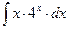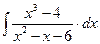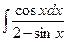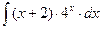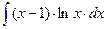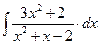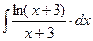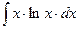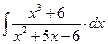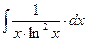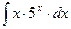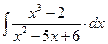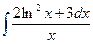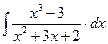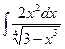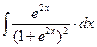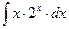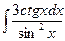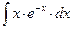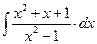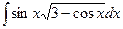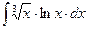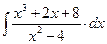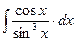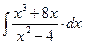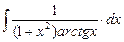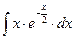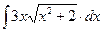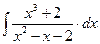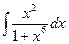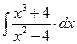Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Розділ. Елементи математичного програмуванняСодержание книги
Поиск на нашем сайте
Тема 4. Задачі лінійного програмування 4.1. Розв’язати систему графічним методом і по можливості знайти вершини утвореної фігури: 1) 4) 7) 4.2. Розв’язати графічним методом задачі лінійного програмування (x1 ≥ 0, x2 ≥ 0): 1) 4) 7) 10) 13) 4.3. Для виготовлення товару A і B підприємство використовує три види сировини I, II, III. Норми витрат сировини на виробництво одного товару кожного виду, ціна одиниці товару A, B а також загальна кількість сировини наведені в наступній таблиці:
Потрібно організувати випуск даної продукції таким чином, щоб прибуток від її реалізації був максимальним. 4.4. Для виготовлення столів та шаф на підприємстві використовується 2 види деревини. Витрати деревини І виду: на стіл 3м3, на шафу 1м3; витрати деревини ІІ виду: на стіл 2м3, на шафу 4м3. Прибуток підприємства від виробництва одного столі становить 10 грн, а шафи 15 грн. Скільки столів і шаф має виготовити підприємство, щоб забезпечити найвищу рентабельність, якщо в його розпорядженні є 9м3 деревини І виду та 16 м3 деревини ІІ виду?
Розділ. Вступ до математичного аналізу. Тема 5. Функціональна залежність. Елементарні функції. Границя функції. Неперервність функції. 5.1. Знайти зазначені границі (не користуючись правилом Лопіталя): 1) 4) 7) 10) 13) 16) 19) 22) 25) 28) 31) 5.2. Дослідити функцію на неперервність: 1) у = 2х2 – 4х + 5; 2) у = х2 + 5х – 1; 3) у = 3х – 2х2. 5.3. Дослідити функцію на неперервність в точках і зробити схематичний малюнок: 1) 3) 5) у = 7) у = Розділ. Диференціальне числення функцій однієї змінної Тема 6. Похідна функції та диференціал. Застосування диференціального числення до дослідження функцій та побудови їх графіків
6.1. Знайти похідні даних функцій: 1) 4) 7) 10) 13) 16) 19) 6.2. Знайти похідні функцій і обчислити їх значення при 1) 3) 5) 6.3. Знайти похідні неявно заданих функцій: 1) 4) 7) 10) 15) 6.4. Знайти похідні степенево-показникової функції: 1) 4) 7) 10) 6.5. Знайти першу та другу похідні функції, заданої параметрично: 1) 4) 7) 6.6. Дослідити функцію на монотонність та екстремум: 1) 6.7. Дослідити функцію та побудувати її графік: 1) 4) 6.8. Знайти диференціали функцій: 1) 6.9. Тіло рухається прямолінійно по закону 6.10. Обсяг продукції 6.11. Залежність між витратами виробництва y (грошові од.) і обсягом продукції, що виробляється x (од.), виражається функцією 6.12. Функції попиту g і пропозиції s від ціни p виражаються відповідно рівняннями а) рівноважну ціну; б) еластичність попиту і пропозиції для цієї ціни; в) зміну доходу (в процентах) при підвищені ціни на 5% від рівноважної.
Розділ. Диференціальне числення функцій багатьох змінних Тема 7. Функції багатьох змінних. Екстремуми функцій багатьох змінних 7.1. Знайти область визначення функції 1) 4) 7) 10) 12) 14) 7.2. Знайти значення функції в точках: 1) 2) 3) 4) 7.3. Знайти границю функції: 1) 3) 7.4. Знайти точки розриву наступних функцій: 1) 4) U = ln (4 - x2 - y2); 5) 7.5. Знайти частинні похідні першого порядку: 1) 4) 7) 10) 13) 15) 17) 19) 21) 23) 7.6. Дано 7.7. Знайти повні диференціали функцій: 1) 4) 7) 7.8. Знайти частинні похідні першого та другого порядку: 1) 4) 7) 7.9. Знайти похідні для даних функцій: 1) 2) 3) 4) 5) 7.10. Знайти критичні точки функції: 1) 3) 5) z = xy - x2 - 2y2 + x + 10y – 8; 6) 7.11. Дослідити функцію на екстремум: 1) 3) 5) 7) 9) 11) 13) 7.12. Знайти умовний екстремум функції: 1) 3) 5) 7.13. Знайти найбільше та найменше значення функції на замкненій області D: 1) 2) 3) 4) 5) 6) 7) 8) 9) 10) 7.14. Дано 7.15. Дано 7.16. Дано Розділ. Інтегральне числення Тема 8.1. Невизначений інтеграл
8.1. Знайти невизначений інтеграл: 1) 4) 8.2. Знайти невизначені інтеграли:
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-06-23; просмотров: 231; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.143.24.110 (0.009 с.) |

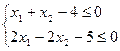 ; 2)
; 2) 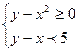 ; 3)
; 3) 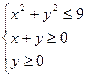 ;
;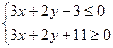 ; 5)
; 5) 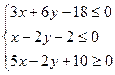 ; 6)
; 6) 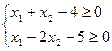 ;
;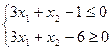 ; 8)
; 8) 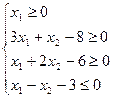
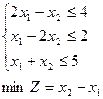 ; 2)
; 2) 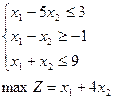 ; 3)
; 3) 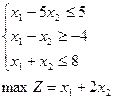 ;
;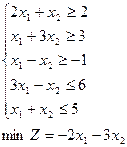 ; 5)
; 5) 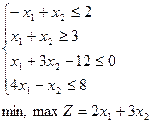 ; 6)
; 6) 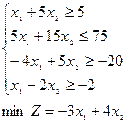 ;
; ; 8)
; 8) 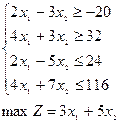 ; 9)
; 9)  ;
;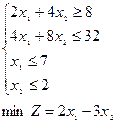 ; 11)
; 11)  ; 12)
; 12) 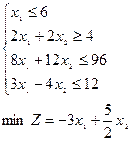 ;
; ; 14)
; 14)  ; 15)
; 15) 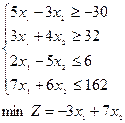

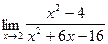 ; 2)
; 2) 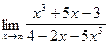 ; 3)
; 3) 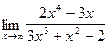 ;
;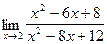 ; 5)
; 5)  ; 6)
; 6) 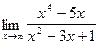 ;
;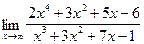 ; 8)
; 8) 
 ; 9)
; 9) 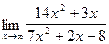 ;
; ; 11)
; 11) 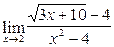 ; 12)
; 12)  ;
;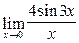 ; 14)
; 14) 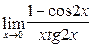 ; 15)
; 15) 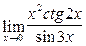 ;
;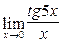 ; 17)
; 17) 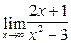 ; 18)
; 18) 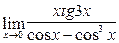 ;
; ; 20)
; 20) 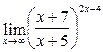 ; 21)
; 21)  ;
;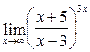 ; 23)
; 23)  ; 24)
; 24) 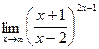 ;
; ; 26)
; 26)  ; 27)
; 27)  ;
;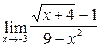 ; 29)
; 29)  ; 30)
; 30)  ;
; ; 32)
; 32)  ; 33)
; 33) 
 ; 2)
; 2) 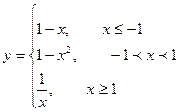 ;
;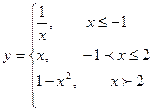 ; 4)
; 4) 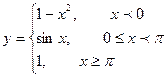 ;
; , х1 = 0, х2 = 1; 6) у =
, х1 = 0, х2 = 1; 6) у =  , х1 = 2, х2 = 3;
, х1 = 2, х2 = 3;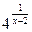 , х1 = 2, х2 = 4;
, х1 = 2, х2 = 4;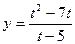 ; 2)
; 2) 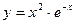 ; 3)
; 3) 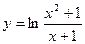 ;
; ; 5)
; 5)  ; 6)
; 6) 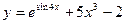 ;
;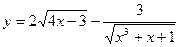 ; 8)
; 8) 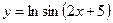 ; 9)
; 9) 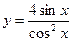 ;
; ; 11)
; 11)  ; 12)
; 12) 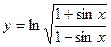 ;
; ; 14)
; 14) 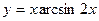 ; 15)
; 15) 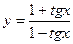 ;
; ; 17)
; 17) 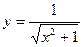 ; 18)
; 18) 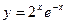 ;
;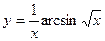 ; 18)
; 18) 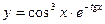
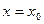 .
.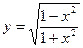 ;
; 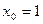 ; 2)
; 2) 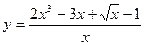 ;
; 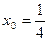 ;
; ;
; 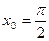 ; 4)
; 4) 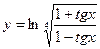 ;
;  ;
;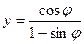 ,
,  ; 6)
; 6) 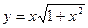 ,
, 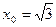 .
.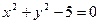 ; 2)
; 2) 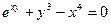 ; 3)
; 3)  ;
; ; 5)
; 5) 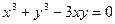 ; 6)
; 6) 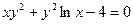 ;
;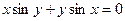 ; 8)
; 8)  ; 9)
; 9) 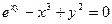 ;
;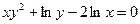 ; 11)
; 11) 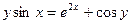 ; 12)
; 12) 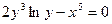 ; 13)
; 13)  ; 14)
; 14) 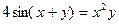 ;
;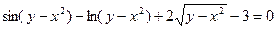
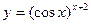 ; 2)
; 2) 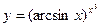 ; 3)
; 3) 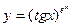 ;
;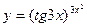 ; 5)
; 5)  ; 6)
; 6) 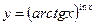 ;
;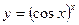 ; 8)
; 8) 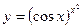 ; 9)
; 9) 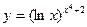 ;
;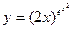 ; 11)
; 11) 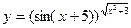 ; 12)
; 12) 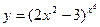
 ; 2)
; 2)  ; 3)
; 3) 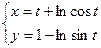 ;
;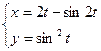 ; 5)
; 5) 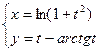 ; 6)
; 6) 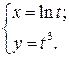
 8)
8) 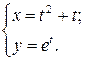 9)
9) 
 ; 2)
; 2) 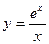
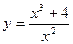 ; 2)
; 2) 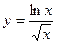 ; 3)
; 3) 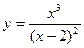 ;
;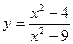 ; 5)
; 5) 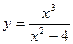
 ; 2)
; 2) 
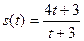 , де
, де 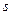 вимірюється в метрах, а t- в секундах. Знайти швидкість і прискорення тіла в момент
вимірюється в метрах, а t- в секундах. Знайти швидкість і прискорення тіла в момент 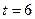 .
.
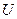 (ум.од.) цеху на протязі робочого дня представляє функцію
(ум.од.) цеху на протязі робочого дня представляє функцію 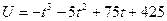 , де t - час (годинах). Знайти продуктивність праці через 2 год. після початку роботи.
, де t - час (годинах). Знайти продуктивність праці через 2 год. після початку роботи. . Визначить середні і граничні витрати при обсязі продукції, що дорівнює 5 од.
. Визначить середні і граничні витрати при обсязі продукції, що дорівнює 5 од.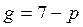 і
і 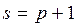 . Знайти:
. Знайти: . Побудувати таку область:
. Побудувати таку область: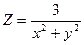 ; 2)
; 2)  ; 3)
; 3) 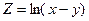 ;
;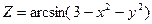 ; 5)
; 5) 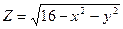 ; 6)
; 6) 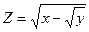 ;
; ; 8)
; 8)  ; 9)
; 9)  ;
;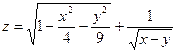 ; 11)
; 11) 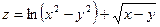 ;
;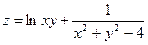 ; 13)
; 13) 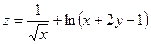 ;
;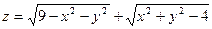 ; 15)
; 15) 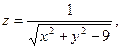
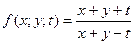 ,
, 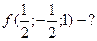 ,
, 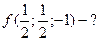 ;
;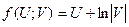 ,
, 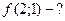 ,
, 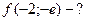 ,
, 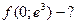 ;
; ,
,  ,
, 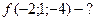 ;
;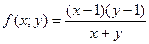 ,
, 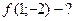 ,
, 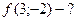 ,
, 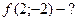
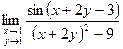 ; 2)
; 2) 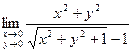 ;
; ; 4)
; 4) 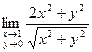 ; 5)
; 5) 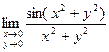
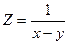 ; 2)
; 2) 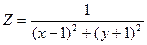 ; 3) U =
; 3) U = 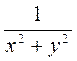 ;
;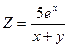 ; 6)
; 6) 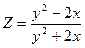
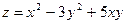 ; 2)
; 2) 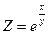 ; 3)
; 3) 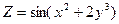 ;
; ; 5)
; 5)  ; 6)
; 6) 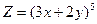 ;
; ; 8)
; 8) 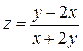 ; 9)
; 9) 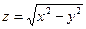 ;
; ; 11)
; 11) 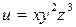 ; 12)
; 12)  ;
;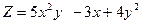 ; 14)
; 14) 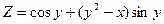 ;
;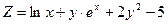 ; 16)
; 16)  ;
;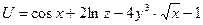 ; 18)
; 18) 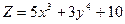 ;
;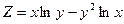 ; 20)
; 20) 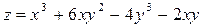 ;
;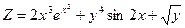 ; 22)
; 22) 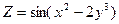 ;
; ;
;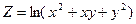 . Довести, що
. Довести, що 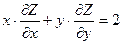 .
. ; 2)
; 2) 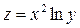 ; 3)
; 3)  ;
;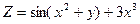 ; 5)
; 5) 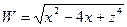 ; 6)
; 6) 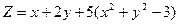 ;
; ; 8)
; 8)  ; 9)
; 9) 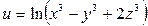
 ; 3)
; 3) 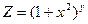 ;
; ; 6)
; 6) 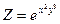 ;
;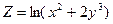 ; 8)
; 8) 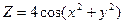
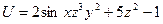 , знайти
, знайти 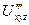 ,
,  ,
, 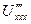 ;
;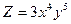 , знайти
, знайти  ,
, 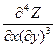 ;
;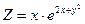 , знайти
, знайти  ,
, 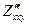 ;
; , знайти
, знайти 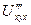 ,
,  ;
;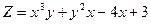 , знайти
, знайти 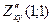
 ; 2)
; 2)  ;
; ; 4)
; 4)  ;
;
 ; 2)
; 2)  ;
;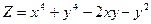 ; 4)
; 4) 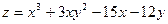 ;
;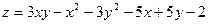 ; 6)
; 6) 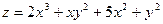 ;
; ; 8)
; 8)  ;
; ; 10)
; 10)  ;
;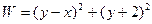 ; 12)
; 12) 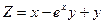 ;
; ; 14)
; 14) 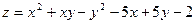
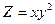 при
при  ; 2)
; 2) 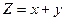 при
при 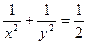 ;
;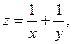 при
при 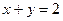 ; 4)
; 4) 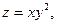 при
при 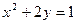 ;
; при
при 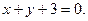
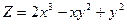 ,
,  ;
; ,
, 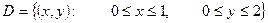 ;
;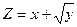 ,
, 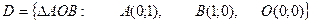 ;
; ,
, 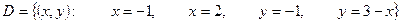 ;
;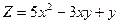 ,
, 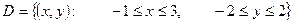 ,
,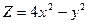 ,
,  ;
;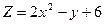 ,
, 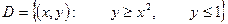 ;
;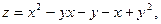
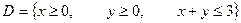 ;
;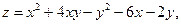
 ;
;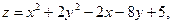
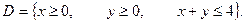
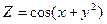 . Довести
. Довести 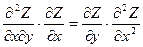
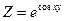 . Довести
. Довести 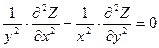
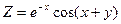 . Довести
. Довести 
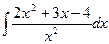 ; 2)
; 2) 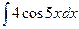 ; 3)
; 3) 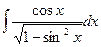 ;
; ; 5)
; 5)  ; 6)
; 6) 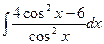 ;
;