
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Свойства неопределенного интегралаСодержание книги
Поиск на нашем сайте
ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИЙ ОДНОЙ ПЕРЕМЕННОЙ
МЕТОДИЧЕСКИЕ УКАЗАНИЯ к практическим занятиям, индивидуальной и самостоятельной работе с заданиями для расчетно-графической работы
Луганск 2008
УДК 681.513:62-50
Составители:
ЛЕВИ ЛЕОНИД ИССАКОВИЧ, доктор технических наук, зав. кафедрой физико-математических дисциплин.
КОВАЛЬ АНАТОЛИЙ ВАСИЛЬЕВИЧ, кандидат физико- математических наук, доцент кафедры физико-математических дисциплин.
Интегральное исчисление функций одной переменной. Методические указания и индивидуальные задания к расчетно-графической работе для студентов инженерных специальностей аграрных университетов/ Леви Л.И., Коваль А.В. – Луганск, ЛНАУ, 2008. – 64 с.
Рецензенты:
ГРИБАНОВ В.М., доктор технических наук, профессор, зав. кафедрой прикладной математики Восточноукраинского национального университета им. В. Даля;
РЕВЕНКО А.В., кандидат физико-математических наук, доцент кафедры физико-математических дисциплин Луганского национального агарного университета.
Издание рассмотрено и рекомендовано к печати: на заседании кафедры физико-математических дисциплин (протокол № 7 от 23 марта 2008 года);
на заседании методической комиссии факультета сельскохозяйственного строительства (протокол № 8 от 19 апреля 2008 года).
СОДЕРЖАНИЕ
I. НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ ……………………………… 5 1.1. Определения и свойства ………………………………………. 5 1.2. Таблица основных интегралов ………………………….......... 7 1.3. Основные методы интегрирования …………………………… 8 1.3.1. Метод непосредственного интегрирования ……………….. 8 Решение типовых примеров по Заданию 1 ….................... 8 1.3.2. Метод замены переменной (метод подстановки) ………… 11 Решение типовых примеров по Заданию 2 ……………….. 12 1.3.3. Метод интегрирования по частям ………………………….. 13 Решение типовых примеров по Заданию 3 ………………… 13 1.3.4. Интегрирование рациональных функций ………………..... 14 Решение типовых примеров по Заданию 4 ……………….. 15 1.3.5. Интегрирование простейших иррациональных функций... 17 1.3.6. Интегрирование тригонометрических функций..……….... 19 Решение типовых примеров по Заданию 5. ………………. 21
2. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ И ЕГО ПРИЛОЖЕНИЯ ……. 23 2.1. Формула Ньютона-Лейбница ………………………………… 23 2.2. Замена переменной в определенном интеграле ……………. 23 2.3. Интегрирование по частям ……………………………………. 23 Решение типовых примеров по Заданию 6 ……………….. 23 2.4. Приложения определенного интеграла ……………………… 24 2.4.1. Вычисление площади плоской фигуры ……………………. 24 Решение типовых примеров по Заданию 7 ……………….. 25 2.4.2. Вычисление длины дуги …………………………………….. 27 Решение типовых примеров по Заданию 8 ……………….. 28 2.4.3. Вычисление объемов тел вращения ……………………….. 29 Решение типовых примеров по Заданию 9 ……………….. 29 Решение типовых примеров по Заданию 10 ……………… 31 ЗАДАНИЯ РАСЧЕТНО-ГРАФИЧЕСКОЙ РАБОТЫ ……..…….. 33 Приложение 1. Номера индивидуальных заданий ……………….. 55 Приложение 2. Таблица производных элементарных функций.. 58 Приложение 3. Формулы по элементарной математике ……….... 59 Приложение 4. Образец титульного листа ………………………... 61 ЛИТЕРАТУРА ……………………………………………………….. 62
I. НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ Определения и свойства Пусть дана функция Определение 1. Функция Например, для функции Всякая непрерывная функция Определение 2. Совокупность всех первообразных Таким образом, по определению
если Функцию Нахождение первообразной для данной функции Правильность интегрирования всегда можно проверить, выполнив обратное действие, т.е. найдя производную функции, получившейся в результате интегрирования. Производная должна быть равна подынтегральной функции.
Таблица основных интегралов 1. В частности, 2. 3. 5. 7. 9. 11. 13. 15. 17. 19. 20. Справедливость этих формул проверяется дифференцированием. Основные методы интегрирования Решение.
Проверка.
е) 1.6. Решение.
Интегрирование по частям Если функции
Решение типовых примеров по Заданию 6 6.1. Решение.
Вычисление длины дуги
Интегрируя дифференциал дуги в заданных пределах, находим длину дуги
где
а длина дуги определяется по формуле
где
Решение типовых примеров по Заданию 8 8.1. Найти площадь фигуры, ограниченной кривыми, заданными в полярных координатах Решение. Площадь криволинейного сектора, ограниченного кривой, заданной в полярных координатах уравнением
8.2. Найти длину дуги параболы Решение. Поскольку
При вычислении интеграла воспользовались формулой 24 таблицы основных интегралов.
8.3. Найти длину дуги кривой Решение. Длина дуги кривой, заданной в полярных координатах, вычисляется по формуле (2.9). В нашем случае
ЗАДАНИЯ РАСЧЕТНО-ГРАФИЧЕСКОЙ РАБОТЫ Задание 1 Найти неопределенные интегралы методом непосредственного интегрирования: Результаты 1.1.
1.2.
1.3.
1.4.
1.5.
1.6.
1.7.
1.8.
1.9.
1.10.
1.11.
1.12.
1.13.
1.14.
1.15.
1.16.
1.17.
1.18.
1.19.
1.20.
1.21.
1.22.
1.23.
1.24.
1.25.
1.26.
1.27.
1.28.
1.29.
1.30.
Задание 2 Найти неопределенные интегралы методом замены переменной 2.1. 2.4. 2.7. 2.10. 2.13. 2.16. 2.19. 2.22. 2.25. 2.28. Задание 3 Найти неопределенные интегралы, используя метод интегрирования по частям 3.1. а) 3.2. а) 3.3. а) 3.4. а) 3.5. а) 3.6. а) 3.7. а) 3.8. а) 3.9. а) 3.10. а) 3.11. а) 3.12. а) 3.13. а) 3.14. а) 3.15. а) 3.16. а) 3.17. а) 3.18. а) 3.19. а) 3.20. а) 3.21. а) 3.22. а) 3.23. а) 3.24. а) 3.25. а) 3.26. а) 3.27. а) 3.28. а) 3.29. а) 3.30. а) |

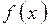 . Необходимо найти такую функцию
. Необходимо найти такую функцию  , производная которой равна
, производная которой равна  .
. если во всех точках этого отрезка выполняется равенство
если во всех точках этого отрезка выполняется равенство 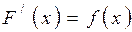 .
. первообразной будет
первообразной будет  потому, что
потому, что  .
. есть также первообразная от
есть также первообразная от  . Здесь
. Здесь  произвольная постоянная.
произвольная постоянная. .
. ,
, подынтегральным выражением;
подынтегральным выражением;  ,
,  .
. ;
;  ;
;  ;
;  .
. .
. . 4.
. 4.  .
. . 6.
. 6.  ..
.. . 8.
. 8.  .
. . 10.
. 10.  .
. . 12.
. 12.  .
. . 14.
. 14.  .
. . 16.
. 16.  .
. . 18.
. 18. 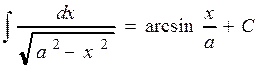 .
. .
. .
. .
.
 .
.

 .
. и
и  имеют непрерывные производные на отрезке
имеют непрерывные производные на отрезке  , то справедлива формула
, то справедлива формула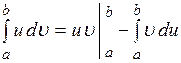 . (2.3)
. (2.3) .
.


 .
. . Если плоская кривая задана в прямоугольной декартовой системе координат уравнением
. Если плоская кривая задана в прямоугольной декартовой системе координат уравнением 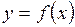 (или
(или  , то дифференциал длины дуги определяется по формуле
, то дифференциал длины дуги определяется по формуле
 .
.
 , (2.8)
, (2.8)
 .
. . Если плоская кривая задана в полярной системе координат уравнением
. Если плоская кривая задана в полярной системе координат уравнением 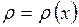 , то дифференциал длины дуги равен
, то дифференциал длины дуги равен ,
, . (2.9)
. (2.9) .
. ;
;  ,
, 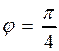 .
. , и двумя полярными радиусами, составляющими с полярной осью углы
, и двумя полярными радиусами, составляющими с полярной осью углы  и
и  вычисляется по формуле (2.7)
вычисляется по формуле (2.7)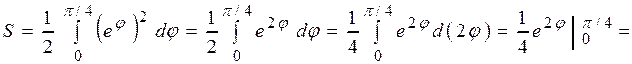
 (кв. ед).
(кв. ед). от точки
от точки  до точки
до точки  .
. , а
, а  , то по формуле (2.8) получим
, то по формуле (2.8) получим
 (ед. длины).
(ед. длины). ;
;  .
. .
.
 (ед. длины).
(ед. длины). сведением интеграла к табличному;
сведением интеграла к табличному; 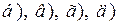 ,
,  пользуясь инвариантностью формулы интегрирования (подведением функции под знак дифференциала).
пользуясь инвариантностью формулы интегрирования (подведением функции под знак дифференциала).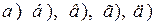 проверить путем нахождения произ-водной от полученной функции.
проверить путем нахождения произ-водной от полученной функции. ;
; 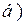
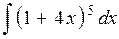 ;
; 
 ;
;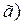
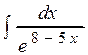 ;
; 
 ;
; 
 .
. ;
;  ;
;  ;
; ;
;  ;
;  .
. ;
;  ;
;  ;
; ;
;  ;
;  .
. ;
;  ;
;  ;
; ;
;  ;
;  .
.
 ;
;  ;
; ;
;  ;
;  .
. ;
;  ;
;  ;
; ;
;  ;
;  .
. ;
;  ;
;  ;
; ;
;  ;
;  .
. ;
;  ;
;  ;
; ;
;  ;
;  .
. ;
;  ;
;  ;
; ;
;  ;
;  .
. ;
;  ;
;  ;
; ;
;  ;
;  .
. ;
;  ;
; 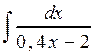 ;
; ;
;  ;
;  .
. ;
;  ;
; 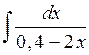 ;
; ;
;  ;
;  .
. ;
;  ;
;  ;
; ;
;  ;
;  .
. ;
;  ;
;  ;
; ;
;  ;
;  .
. ;
;  ;
;  ;
; ;
;  ;
;  .
. ;
;  ;
;  ;
; ;
;  ;
;  .
. ;
;  ;
; 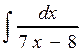 ;
; ;
;  ;
;  .
.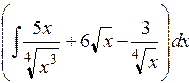 ;
;  ;
;  ;
; ;
;  ;
;  .
.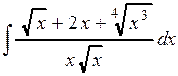 ;
;  ;
; 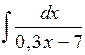 ;
; ;
;  ;
;  .
. ;
;  ;
;  ;
;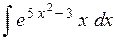 ;
;  ;
;  .
. ;
;  ;
;  ;
; ;
;  ;
;  .
.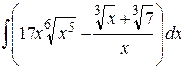 ;
;  ;
;  ;
; ;
;  ;
;  .
. ;
; 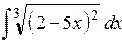 ;
;  ;
; ;
;  ;
;  .
. ;
;  ;
;  ;
; ;
; 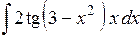 ;
;  .
. ;
;  ;
;  ;
; ;
;  ;
;  .
. ;
;  ;
;  ;
; ;
;  ;
;  .
. ;
;  ;
;  ;
;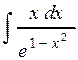 ;
;  ;
;  .
. ;
;  ;
;  ;
; ;
;  ;
;  .
. ;
;  ;
;  ;
; ;
;  ;
;  .
. ;
;  ;
;  ;
; ;
;  ;
;  .
. . 2.2.
. 2.2.  . 2.3.
. 2.3.  .
. . 2.5.
. 2.5.  . 2.6.
. 2.6.  .
. . 2.8.
. 2.8. 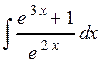 . 2.9.
. 2.9.  .
. . 2.11.
. 2.11. 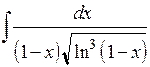 . 2.12.
. 2.12. 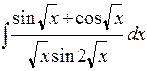 .
. . 2.14.
. 2.14.  . 2.15.
. 2.15.  .
. . 2.17.
. 2.17.  . 2.18.
. 2.18.  .
. . 2.20.
. 2.20.  . 2.21.
. 2.21.  .
. . 2.23.
. 2.23.  . 2.24.
. 2.24.  .
. 2.26.
2.26.  . 2.27.
. 2.27. 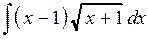 .
. . 2.29.
. 2.29.  . 2.30.
. 2.30. 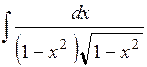 .
. ; б)
; б)  .
. ; б)
; б)  .
. ; б)
; б)  .
. ; б)
; б)  .
. ; б)
; б)  .
. ; б)
; б)  .
. ; б)
; б)  .
. ; б)
; б)  .
. ; б)
; б)  .
. ; б)
; б)  .
. ; б)
; б)  .
. ; б)
; б)  .
.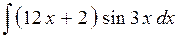 ; б)
; б)  .
. ; б)
; б)  .
.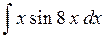 ; б)
; б)  .
. ; б)
; б)  .
. ; б)
; б)  .
. ; б)
; б)  .
. ; б)
; б)  .
. ; б)
; б) 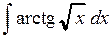 .
. ; б)
; б)  .
. ; б)
; б)  .
. ; б)
; б)  .
. ; б)
; б)  .
. ; б)
; б)  .
.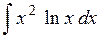 ; б)
; б)  .
. ; б)
; б)  .
. ; б)
; б)  .
. ; б)
; б) 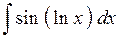 .
.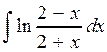 ; б)
; б) 


