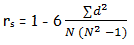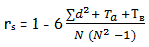Средние значения оценок избирателей и индивидуальные показатели депутата

Наименование качества	Средние оценки избирателей (эталонный профиль) (А)	Ранг А	Показатели депутата (В)	Ранг В	d	d^2
Ответственность	9,56				-1
Порядочность	9,02			8,5	-6,5	42,25
Общительность	8,74			13,5	-10.5	110,25
Выдержка/самообладание	8,71				-8
Общий уровень культуры	8,64
Энергичность/активность	8,41
Логика	8,38			8,5	-1,5	2,25
Самокритичность	8,28
Самостоятельность	8,12
Личностная зрелость	8,10
Целеустремленность	8,00
Обучаемость	7,89	12,5			-2,5	6,25
Гуманизм	7,89	12,5			1,5	2,25
Толерантность	7,84				-0,5	0,25
Стойкость	7,74
Гибкость поведения	7,67				-2
Способность производить благоприятное впечатление	7,23			13,5	3,5	12,25
Креативность	6,27
∑						483,75

Правила ранжирования: большему значению – меньший ранг

Сформулируем гипотезы

Н₀ – корреляция между индивидуальными показателями депутата и эталонными показателями не отличаются

Н₁ – корреляция между индивидуальными показателями депутата и эталонными показателями статистически значимо отличаются

Поскольку в обоих рангах присутствуют одинаковые – необходимо внести поправки.

В ряду А присутствует 1 группа одинаковых рангов

А = 2 (количество одинаковых рангов)

А и В – количество одинаковых рангов

Коэффициент Спирмана:

Коэффициент Спирмана при одинаковых рангах:

Далее нужно сравнивать результаты с критическими значениями:

Табличные значения:

1. Смотрится по n (чему оно равно)

2. r_кр = 0,47

Нужно сравнить показатели

r_{эмп >} r_кр

Ответ:

Гипотеза Н₀ отвергается, принимаем Н₁. Депутат не соответствует эталонному профилю избирателей. Статистически значимо отличие эталонного профиля избирателей и индивидуальный профиль кандидата в депутаты, т.к. имеются расхождения по шкалам …. этими расхождениями объясняется снижение коэффициента Спирмана.

14. Корреляционная матрица, ее особенности.
Корреляционная матрица и ее особенности.

Корреляционная матрица – это матрица, дающая коэффициент корреляция между каждой переменной в наборе данных в каждой другой переменной этого набора.

	V1	V2	V3	V4	V5
V1		0,5	0,444
V2	0,5		0,300
V3	0,444	0,300
V4
V5

Особенности матрицы:

1. Матрица корреляции симметрична относительно своей главной диагонали

2. Диагональ составляет единицу – коэффициент корреляции данного признака с самим собой

3. Испытуемые и их порядковые номера из таблицы сводных данных в матрицы корреляций уже никак не представлены

4. Коэффициент корреляции несет информацию только о силе и направленности связей между признаками и не дают никаких сведений ни об одном отдельном испытуемом

5. Корреляционную матрицу наглядно представить в виде корреляционной плеяды и описать в тексте

Описывание в тексте полученные связи:

1. Констатируем связь

2. Какова направленность связи (положительная и отрицательная)

3. Уровень достоверности при уровне значимости

4. Сила связи

Задание

Используя формула расчет коэффициент Пирсона рассчитать сопряженность между цветом волос и цветом глаз в данной выборке.

Были собраны следующие данные:

Совместное распределение частот цвета волос и цвета глаз

Цвет глаз	Цвет волос
Светлые	Русые	Черные	Рыжие	∑
Голубые
Серые
Карие
∑

Алгоритм расчета:

1. Рассчитать сумму отношений квадратов частот каждой клетки таблицы к произведению итоговых частот соответствующего столбца и строки

2. Вычислить показатель взаимной сопряженности по формуле

3. Подставим полученные данные в формулу

Ответ:

Связь между цветом волос и цветом глаз в данной выборке прямая и слабая (мы не можем по цвету глаз определить с точностью какой будет цвет волос и наоборот).

15. Дисперсионный однофакторный. Отличие дисперсионного анализа
корреляционного. Этапы подготовки данных к дисперсионному анализу.
Дисперсионный анализ.

Методы многомерного анализа: регрессионный, дисперсионный, факторный анализ.

Позволяют выделить срытые переменные, признаки и внутреннюю структуру связей между ними.

Независимая переменная – фактор, который изменяется или учитывается исследователем (возврат испытуемых).

Зависимая переменная – результативный признак, отклик на изменение независимой переменой. (обучаемость и эффективность выполнения задачи)

Дисперсионный анализ – это анализ изменчивости признака (з/п) под влиянием каких-либо контролируемых факторов (н/п).

Метод основан на сравнении дисперсий. Если различия между дисперсиями значимы, то фактор оказывает существенное влияние на признак. ANOVA – анализ вариативности.

Автором методом является Фишер.

Критерия Фишера является параметрическим, потому что в формулу расчета входят оценки дисперсий. В дисперсионном анализе исследователь исходит из положения, что они переменные могут рассматриваться как причины, а другие как следствие.

Ближайшим и более простым аналогом ANOVA является Т-критерий Стьюдента (тоже параметрический критерий), но в отличии от Т-критерия, дисперсионный анализ предназначен для сравнения не 2х выборок, а больше.

Есть несколько видов анализа:

1. Однофакторный дисперсионный анализ (one way) – в этой команде можно задать одну независимую переменную, всегда номинативную и имеющую несколько градаций (низкое, среднее, высокое). Можно задать 1 независимую переменную, которая группирует объекты заданной выборки в сравниваемой выборке и задать несколько зависимых переменных (они всегда количественного или метрического типа)

· Связанная выборка

· Несвязанная выборка

2. Многофакторный (МANOVA) – позволяет анализировать как множество зависимых, так и множество зависимых переменных

Подготовка данных к дисперсионному анализу:

1. Создание комплексов – для каждого испытуемого создается отдельная карточка, куда вносятся все его данные по всем измеренным признакам

2. Уравновешивание комплексов - равномерный комплекс тот, в котором каждая ячейка представлена одинаковым количеством наблюдений. В случае если оказалось неравное количество наблюдений, необходимо отсеять некоторые из них

3. Проверка нормальности распределения признака.

Алгоритм дисперсионного анализа для связанной выборки:

1. Назначение метода – метод дисперсионного анализа для связанных выборок применяется в тех случаях, когда исследуется влияние одного фактора на одну и ту же выборку испытуемых. Градации фактора должно быть не менее 3х. Это лонгитюдный метод

2. Описание метода

Пример:

Группа из 5 испытуемых была обследована с помощью 3х экспериментальных заданий, направленных на изучение интеллектуальной настойчивости. Каждому испытуемому индивидуально предъявлялись последовательно 3 одинаковые анаграммы (4, 5, 6-буквенные). Можно ли считать, что фактор длины анаграммы влияет на длительность попыток решения или же будут влиять другие факторы.