
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Опред., св-ва и прим. вект-х пр-в.
Опред., св-ва и прим. вект-х пр-в. Числ-е поле Р – мн-во R или C. Внутр. операции – двум эл-м из L соотв-ет третий из L(x+y=z).Внешн. – каждому x из L и каждому α из Р соотв-ет некоторый эл-т из L(αx=z)/ Мн-во L эл-в x,y,z, … наз-ся лин. пр-вом, если в нём определены внутрен. (x+y) и внешн. (αx) опер. удовл-щие аксиомам: 1.x+y=y+x, "x,yєL; 2.(x+y)+z=x+(y+z), "x,y,zєL; 3.$ нейтр-ный эл-т 4.x є L $ -xє L: x+(-x)= 5.α(x+y)=αx+αy "x, y є L; α,βєP; 6.(α+β)x=αx+βx "x є L; α,βєP; 7.α(βx)=(αβ)x "x є L; α,βєP; 8.1*x=x "x є L. Св-ва лин. пр-ва 1.В лин. пр-ве L над полем P $ ед-ный нейтр. эл-т. (пусть $ 2." xєL ед-ный –xєL(пусть $ -x и 3.0*x= 4.(-1)x=-x "x є L( Примеры: Эл-ты любой природы,удовл-щие двум правилам и 8 аксиомам.Напр., совок-ть любых матриц mxn c действит. эл-тами(P=R). Мн-во свободных векторов трёхмерного пр-ва – L, P=R. Лин. пр-во наз-ся пустым,если состоит из нулевого эл-та.
Лин-я зависимость системы векторов.
Пр.1 L=C; P=R; Св-ва 1 Система (1) сод-т 0 вектор, то она лин. зависима( 2 Система (1) сод-т лин. зависимую подсистему, то и сама система лин. зависима. 3 Система линейно зависима, то по крайней мере 1 из векторов этой системы выр-ся в виде лин. комбинации остальных векторов. 4 Пусть система (1) лин. независима а набор
Базис лин. пр-ва, размерность. Коорд-ты. Базисом в пр-ве L над полем Р наз-ся система в-ров 1Система (1) лин. независима; 2"xϵL $ Коорд. в-ра х в базисе (1) – числа Св-ва: 1Если коорд. вектора в некотором базисе =0,то это нулевой вектор. 2 3Коорд. в-ров в заданном базисе определяются однозначно. 4 При сложении векторов их коорд. заданные в одном и том же базисе складываются. 5При умножении вектора на число, его коорд. умн-ся на число. Число k наз-ся размерностью лин. пр-ва L, если в L сущ-ет система из k лин. независимых векторов, а любая система из k +1 вектора — лин. зависима.
Обозначается dim L = k. Пр-во L наз-ся k -мерным. Иногда обозначается L k.
Матрич.запись коо вект-в, изм. коо при замене базиса Вект. х(λ1,..,λn) в некот.базисе (е1,..,еn).обозначим Х=(λ1,..,λn)Т и [e]= (е1,..,еn), эл-ми явл. базисн. вект. Тогда вект. Х можно предст. след.обр. х=[e]Х=х1е1+..+ хnеn т.е это разлож. вектора х по базису. Т. для того, чтобы вект. х1, х2,.., хп были лин.зав. необх. и дост., чтобы коо-столбцы этих вект. В некот. Базисе были лин.зав. Т. матричн.критерий. для того,чтобы вект. Были лин.зав., необх и дост, чтобы матрица, сост. из коо. Столбцов этих вект. В некот.базисе была меньше числа вект. Преобр.базисов и коо. Пусть им-ся 2 базиса[e]=[е1,..,еn], [e’]=[е1’,..,еn’]в одном пр-ве L над P.выразим коо штрих. базиса ч/з коо нештрих.
Св-ва матрицы перех: 1.матрица перех. Опр-ся однозначно. Это след-ет из одно-ти разлож. Вект-в по бизасу. 2. матрица перех. невырожденн. Это след-ет из матричн.критерия лин.зав-ти вект-в. 3. матрица перех. от базиса [e]к[e] единичная 4. пусть Т-матрица перех.от [e]к [e’]. А матрица Q от [e’]к [e’’].Тогда матрица перех от [e]к [e’’] будет TQ. 5. если Т-матрица перех. от [e]к [e’],то T-1есть матрица перех. от[e’] к [e]. Преобр. коо вект-в при перех. К новому базису Псть даны базисы [e], [e’] и матрица Т, т.е. [e’]=[e]T. Возьмем произв.вектор х и его можно предст. х=[e]Х=[e’]Х’; [e]Х=[e]TХ’=> поск-ку коо вект-ра в данном базисе опр-ся однозначно X=TX’ Матрица лин. оп-ра. Изменение матр. оп-ра при замене базиса.
[
Матр. А, удовлетворяющая рав-ву (2’) наз-ся матр. лин. оп-ра в базисе (1). Матр. лин. оп-ра в баз. (1) – матр., столбцами которой явл-ся коорд. столбцы образов базисных вект. в этом же баз. Рассмотрим мн-во всех лин. оп-ров, кот. действуют из Связь между коорд. вект. и его образом в заданн. баз.
[
Изменение матр.лин. оп-ра при измен. баз. Пусть
Матр. Т.2. Подобные матр. имеют равные определители. ЕВКЛИДОВЫ ПРОСТРАНСТВА. ОПРЕДЕЛЕНИЕ, ПРИМЕРЫ ОПР: скалярное произведение двух векторов а и b в линейном пространстве L над полем Р - действительное число. Обозначается (а, b) и удовлетворяет следующим аксиомам: 1 (а, b) = (b, а) для любого а, b принадлежащего L 2 ((а + b), с) = (а, с) + (b, с) для любых а,b,c принадлежащих L 3 ((α a), b) = α (а, b)для любого а, b принадлежащего L, для любого α принадлежащего R 4 (а, а) ≥ 0, (а, а)= 0 в том и только том случае, если а = 0 Следстивие 1: для любых а,b,c принадлежащих L (а, (b + с)) = (а, b) + (a, с) Доказательство: (а, (b + с)) = 1)= ((b + с), а)= 2)= (b, а) + (с, а) = 1)= (а, b) + (a, с) чтд Следствие 2:для любого а, b принадлежащего L, для любого α принадлежащего R (а, α b) = α (а, b) Следствие 3.
Пример. Опред. Линейное пр-во L над полем R наз Евклидовым, если в нём определена операция скалярного произведения. Замечание. В пр-ве L над полем С также может быть введено понятие скалярного произведения, Т. В любом Евклидовом пр-ве справедливо нер-во Каши-Буняковского
Следствие.
Опред., св-ва и прим. вект-х пр-в. Числ-е поле Р – мн-во R или C. Внутр. операции – двум эл-м из L соотв-ет третий из L(x+y=z).Внешн. – каждому x из L и каждому α из Р соотв-ет некоторый эл-т из L(αx=z)/ Мн-во L эл-в x,y,z, … наз-ся лин. пр-вом, если в нём определены внутрен. (x+y) и внешн. (αx) опер. удовл-щие аксиомам: 1.x+y=y+x, "x,yєL; 2.(x+y)+z=x+(y+z), "x,y,zєL; 3.$ нейтр-ный эл-т 4.x є L $ -xє L: x+(-x)= 5.α(x+y)=αx+αy "x, y є L; α,βєP; 6.(α+β)x=αx+βx "x є L; α,βєP; 7.α(βx)=(αβ)x "x є L; α,βєP; 8.1*x=x "x є L. Св-ва лин. пр-ва 1.В лин. пр-ве L над полем P $ ед-ный нейтр. эл-т. (пусть $ 2." xєL ед-ный –xєL(пусть $ -x и 3.0*x= 4.(-1)x=-x "x є L( Примеры: Эл-ты любой природы,удовл-щие двум правилам и 8 аксиомам.Напр., совок-ть любых матриц mxn c действит. эл-тами(P=R). Мн-во свободных векторов трёхмерного пр-ва – L, P=R. Лин. пр-во наз-ся пустым,если состоит из нулевого эл-та.
|
||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 211; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.21.12.41 (0.006 с.) |
 x "x є L;
x "x є L;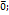
 и
и 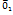 ,
,  )
) , тогда x+(-x)=
, тогда x+(-x)=  , x+
, x+  ).
).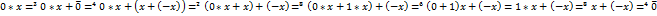 );
); ).
). ,
,  , …,
, …,  (1) – заданные в-ры из L. Система (1) лин. зависима, если сущ-ет ненулевой набор чисел
(1) – заданные в-ры из L. Система (1) лин. зависима, если сущ-ет ненулевой набор чисел 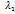 ,
,  (не все
(не все  =0):
=0):  =
=  (2) Система наз-ся лин. независимой, если рав-во (2) возможно только в том случае, когда все
(2) Система наз-ся лин. независимой, если рав-во (2) возможно только в том случае, когда все 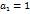 ,
,  =i;
=i; 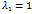 ,
,  . 1*1+i*i=0 Пр.2Возьмём L=C; P=R;
. 1*1+i*i=0 Пр.2Возьмём L=C; P=R;  =i;
=i;  +
+  =0 <=>
=0 <=>  ,
, 
 ; l1=…=ln-1=0, ln=1; 0*a1+…+0*an-1+1*
; l1=…=ln-1=0, ln=1; 0*a1+…+0*an-1+1*  лин. зависим, тогда x можно выразить через векторы (1).
лин. зависим, тогда x можно выразить через векторы (1). (1), удовл-я усл-ям:
(1), удовл-я усл-ям: : x=α1a1+α2a2+…+αnan(2)
: x=α1a1+α2a2+…+αnan(2) во всяком базисе имеет нулевые коорд.
во всяком базисе имеет нулевые коорд. коо в нештрих.базисе штрих-го. Матрица Т наз-ся матрицей перехода от [e]к[e’] [e’]=[e]T. – связь между двумя базисами
коо в нештрих.базисе штрих-го. Матрица Т наз-ся матрицей перехода от [e]к[e’] [e’]=[e]T. – связь между двумя базисами - преобразователь пр-ва. Пусть
- преобразователь пр-ва. Пусть 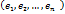 - базис (1)
- базис (1) (2)
(2)

 (2’)
(2’) . Каждому лин. оп-ру ставится в соответств. в заданн. баз. некоторая матр. М. В данном баз. можно установить взаимнооднозначн. соответств. между матриц., действующ. из
. Каждому лин. оп-ру ставится в соответств. в заданн. баз. некоторая матр. М. В данном баз. можно установить взаимнооднозначн. соответств. между матриц., действующ. из  . Пусть
. Пусть  , где
, где  - коорд. столб.
- коорд. столб.

 =
=  =
=  .
. (2)- два базиса в пр-ве
(2)- два базиса в пр-ве  .
.  и
и  - соотв. матр. оп-ра
- соотв. матр. оп-ра  . (3)
. (3) и
и 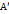 , связанные рав-вом (3), где Т- невырожд. матр., наз-ся подобными.
, связанные рав-вом (3), где Т- невырожд. матр., наз-ся подобными.



 в соответствие ставится комплексное число(такое пр-во наз комплексным Евклидовым или унитарным) и изменяется 1-я аксиома
в соответствие ставится комплексное число(такое пр-во наз комплексным Евклидовым или унитарным) и изменяется 1-я аксиома  /
/





