
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Равновесное тепловое излучение.Содержание книги
Поиск на нашем сайте
Если создать некоторую оболочку, непрозрачную для электромагнитных волн, и будем поддерживать ее при постоянной температуре, то внутри ее установится равновесие. Вся энергия, излучаемая внутренней поверхностью оболочки, будет ею же и поглощаться. Излучение в адиабатически замкнутой системе (не обменивающейся теплотой с внешней средой) называется равновесным. Если создать маленькое отверстие в стенке полости состояние равновесия измениться слабо и выходящее из полости излучение будет соответствовать равновесному излучению. Если в такое отверстие направить луч, то после многократных отражений и поглощения на стенках полости он не сможет выйти обратно наружу. Это значит, что для такого отверстия коэффициент поглощения a (l, T) = 1. Рассмотренная замкнутая полость с небольшим отверстием служит одной из моделей абсолютно черного тела. Абсолютно черным телом называется тело, которое поглощает все падающее на него излучение независимо от направления падающего излучения, его спектрального состава и поляризации (ничего не отражая и не пропуская). Для абсолютно черного тела, спектральная плотность энергетической светимости является некоторой универсальной функцией длины волны и температуры f(l,T) и не зависит от его природы. Все тела в природе частично отражают падающее на их поверхность излучение и поэтому не относятся к абсолютно черным телам. Если коэффициент монохроматического поглощения тела одинаков для всех длин волн и меньше единицы (a(l, T) = aТ = const<1), то такое тело называется серым. Коэффициент монохроматического поглощения серого тела зависит только от температуры тела, его природы и состояния его поверхности. Кирхгофом было показано, что для всех тел, независимо от их природы, отношение спектральной плотности энергетической светимости к коэффициенту монохроматического поглощения является той же универсальной функцией длины волны и температуры f(l,T), что и спектральная плотность энергетической светимости абсолютно черного тела:
Уравнение (3) представляет собой закон Кирхгофа. Закон Кирхгофа можно сформулировать таким образом: для всех тел системы, находящихся в термодинамическом равновесии, отношение спектральной плотности энергетической светимости к коэффициенту монохроматического поглощения не зависит от природы тела, является одинаковой для всех тел функцией, зависящей от длины волны l и температуры Т. Из вышесказанного и формулы (3) ясно, что при данной температуре сильнее излучают те серые тела, которые обладают большим коэффициентом поглощения, а наиболее сильно излучают абсолютно черные тела. Так как для абсолютно черного тела a(l, T)=1, то из формулы (3) следует, что универсальная функция f (l, T) представляет собой спектральную плотность энергетической светимости абсолютно черного тела
Законы излучения абсолютно черного тела
Формула Планка.
Выражение для спектральной плотности энергетической светимости абсолютно черного тела было получено впервые немецким физиком М. Планком. Согласно квантовой гипотезе Планка испускание энергии электромагнитных волн атомами вещества может происходить только отдельными "порциями" - квантами. При этом энергия кванта света пропорциональна его частоте n:
Постоянная h была названа постоянной Планка, c -скорость света в вакууме. На основании этой гипотезы, используя статистические методы, он получил следующую формулу для универсальной функции f, в которую входит энергия кванта h n:
где k -постоянная Больцмана. Формулу для универсальной функции, зависящей от длины волны l (а не от частоты n) можно вывести используя определение спектральной плотности энергетической светимости
Знак “минус” здесь не играет существенной роли и отражает тот факт, что d n dl имеют разные знаки (т.е. если l увеличивается, n уменьшается) Следовательно,
Рис.1 Зависимость спектральной плотности энергетической светимости абсолютно черного тела от длины волны. Примечание: На рисунке заштрихован интервал длин волн, соответствующий видимому свету. На рис.1 представлены графики f(l, T) для различных температур. Формула (5*) хорошо согласуется с экспериментальными данными во всем интервале наблюдаемых длин волн и температур и называется формулой Планка. Основные законы излучения абсолютно черного тела можно получить из формулы Планка. Однако многие из них получены на основе экспериментальных данных, а также представлений классической физики еще до открытия Планком своей формулы. Поэтому эти закономерности носят имя ученых, открывших их, и формулируются в виде законов.
Закон смещения Вина.
Из рис.1 видно, что максимум спектральной плотности энергетической светимости с ростом температуры смещается в сторону более коротких волн. Чтобы найти закон смещения данного максимума, необходимо продифференцировать выражение (5) по l и приравнять производную к нулю. Из полученного уравнения можно найти длину волны соответствующую максимуму спектральной плотности энергетической светимости абсолютно черного тела как функцию температуры:
где b - постоянная Вина, lmax - длина волны, соответствующая максимальному значению спектральной плотности энергетической светимости
Закон Вина можно сформулировать следующим образом: д лина волны, соответствующая максимальному значению спектральной плотности энергетической светимости абсолютно черного тела, обратно пропорциональна его температуре.
2.3.3. Закон Рэлея-Джинса.
Для больших длин волн, когда показатель экспоненты в формуле Планка (5) значительно меньше единицы, экспоненту можно разложить в ряд и ограничиться двумя членами разложения:
Теперь, если подставить (8) в (5), получим:
Эта формула, получившая название формулы Рэлея-Джинса, хорошо описывает тепловое излучение абсолютно черного тела на длинах волн, удовлетворяющих условию:
Рэлей и Джинс получили эту формулу до открытия Планка, основываясь на представлении о непрерывном характере испускания электромагнитных волн и на законе о равномерном распределении энергии по степеням свободы. Формула Рэлея-Джинса верна для длинных волн и совершенно не применима для коротких.
Закон Стефана – Больцмана
В 1879 г. Стефан из анализа экспериментальных результатов, а в 1884г. Больцман из термодинамических представлений получили зависимость энергетической светимости абсолютно черного тела от температуры:
R(T)=σT 4 (11)
где постоянная σ =5.67 10-8 Вт/(м2 К4) - постоянная Стефана-Больцмана. Из выражения (11) можно сформулировать закон Стефана-Больцмана: Энергетическая светимость абсолютно чёрного тела пропорциональна четвёртой степени его термодинамической температуры. Формулу (11) можно получить, используя формулу Планка (5). Для этого необходимо в формулу (1) подставить выражение (5) и провести интегрирование по всем длинам волн (от нуля до бесконечности):
Введем новую переменную:
Подставив (13) в (12), получим:
Если учесть, что значение несобственного интеграла в (14) равно π 4/15, получим:
Из сравнения (11) с (15) следует, что постоянная Стефана-Больцмана равна:
Оптическая пирометрия. Оптической пирометрией называется совокупность методов измерения температуры тел, основанных на законах теплового излучения. Приборы, применяемые для этого, называются пирометрами. Эти методы очень удобны для измерения температур различных объектов, где сложно или вообще невозможно применить традиционные контактные датчики. Это относится в первую очередь к измерению высоких температур. В оптической пирометрии различают следующие температуры тела: радиационную, цветовую, яркостную. Радиационная температура. Радиационная температура Тр - это температура абсолютно чёрного тела, при которой его энергетическая светимость R равна энергетической светимости Rm данного тела в широком диапазоне длин волн. Если же измерить мощность, излучаемую некоторым телом с единицы поверхности в достаточно широком интервале волн и ее величину сопоставить с энергетической светимостью абсолютно черного тела, то можно, используя формулу (11), вычислить температуру этого тела, как
Определенная таким способом температура Tp будет достаточно точно соответствовать истинной температуре T при условии, что коэффициент монохроматического поглощения поверхности тела должен быть близок к единице. Для реальных (нечерных) тел истинная температура Т оказывается больше радиационной Тр. Например, для серого тела закон Стефана-Больцмана может быть записан в виде Rm(T) = αT σT 4; Подставляя данное выражение в формулу (17), получим
Из (18) следует, что истинная температура серого тела всегда выше радиационной, т.е. Tp < T.
3.2. Цветовая температура.
Спектральная плотность энергетической светимости серых тел (или тел близких к ним по свойствам) с точностью до постоянного коэффициента (коэффициента монохроматического поглощения) пропорциональна спектральной плотности энергетической светимости абсолютно черного тела. Следовательно, распределение энергии в спектре серого тела такое же, как и в спектре абсолютно черного тела при той же температуре. Для определения температуры серого тела достаточно измерить мощность I(λ,Т), излучаемую единицей поверхности тела в достаточно узком спектральном интервале (пропорциональную r(λ,Т)), для двух различных волн. Отношение I(λ,Т) для двух длин волн равно отношению зависимостей f(λ,Т) для этих волн, вид которых дается формулой (5):
Из данного равенства можно математическим путем получить температуру Т. Полученная таким образом температура называется цветовой. Цветовая температура тела, определенная по формуле (19), будет соответствовать истинной, если коэффициент монохроматического поглощения не сильно зависит от длины волны. В противном случае понятие цветовой температуры теряет смысл. Цветовая температура серого тела совпадает с истинной температурой и может быть найдена также из закона смещения Вина. Таким образом, цветовая температураТц - это температура абсолютно чёрного тела, при которой относительные распределения спектральной плотности энергетической светимости абсолютно чёрного тела и рассматриваемого тела максимально близки в видимой области спектра. Обычно для определения цветовой температуры выбирают длины волн λ1=655 нм (красный цвет), λ2= 470 нм (зелено-голубой цвет).
3.3. Яркостная температура.
Яркостной температурой Тя некоторого теланазывается температура абсолютно чёрного тела, при которой его спектральная плотность энергетической светимости r(λ,T) для какой либо определённой длины волны равна спектральной плотности энергетической светимости rТ(λ,Т) данного тела для той же длины волны. Так как для нечерного тела спектральная плотность энергетической светимости при определенной температуре будет всегда ниже чем у абсолютно черного тела, то истинная температура тела будет всегда выше яркостной. В качестве яркостного пирометра широко используется пирометр с исчезающей нитью. Принцип определения температуры основан на визуальном сравнении яркости раскаленной нити лампы пирометра с яркостью изображения исследуемого объекта. Равенство яркостей, наблюдаемое через монохроматический светофильтр (обычно измерения проводят на длине волны λ =660 нм), определяется по исчезновению изображения нити пирометрической лампы на фоне изображения раскаленного объекта. Накал нити лампы пирометра регулируется реостатом, а температура нити определяется по градуировочному графику, или таблице. Если температура нити высока, то для ослабления потока излучения применяется также и нейтральный светофильтр. Пусть мы в результате измерений получили равенство яркостей нити пирометра и исследуемого объекта и по графику определили температуру нити пирометра Т1. Тогда, на основании формулы (3) можно записать: f (λ,T1) α1 (λ,T1) = f (λ,T2) α2 (λ, T2 ) (20)
где α1 (λ,T1) и α2 (λ,T2) коэффициенты монохроматического поглощения материала нити пирометра и исследуемого объекта соответственно; T1 и T2 – температуры нити пирометра и объекта. Как видно из (20), равенство температур объекта и нити пирометра будут наблюдаться только тогда, когда будут, равны их коэффициенты монохроматического поглощения в наблюдаемой области спектра α1 (λ,T1) = α2 (λ,T2). Если α1 (λ,T1) > α2 (λ,T2), мы получим заниженное значение температуры объекта, при обратном соотношении - завышенное значение температуры.
4. Определение постоянной Стефана-Больцмана с помощью оптического пирометра Для реальных (не черных, в том числе и серых) тел на основании закона Стефана-Больцмана можно определить мощность излучения во всем интервале длин волн W: W = α(Т) S σТ 4 (21) где S – площадь поверхности нагретого тела; αТ – коэффициент черноты реального тела. Он равен отношению энергетической светимости данного реального тела к энергетической светимости абсолютно черного тела при той же температуре. Данный коэффициент представляет интегральный (по всем длинам волн) коэффициент поглощения реального тела. Для серого тела этот коэффициент представляет собой коэффициент монохроматического поглощения α Т, не зависящий от длины волны (введен ранее в 2.2). В качестве тела-источника теплового излучения можно взять вольфрамовую спираль вакуумной лампы накаливания. Подводимая энергия электрического тока в такой лампе расходуется в основном на тепловое излучение. Доля рассеиваемой мощности лампы за счет теплопроводности составляет небольшую величину и ею можно пренебречь в общем балансе энергии. Таким образом, с одной стороны, мы можем определить мощность излучения из закона Джоуля-Ленца, с другой, определить температуру нити лампы с помощью оптического пирометра. При этом температура, определенная с помощью пирометра, будет истинной, поскольку нити лампы пирометра и исследуемой лампы изготовлены из одного материала - вольфрама. Поэтому можно записать: W= Iл Uл = αТ S б Т4 (22)
где Iл, Uл - ток и напряжение питания лампы. Зная длину и диаметр нити накала, а также коэффициент черноты αТ вольфрама в видимой области спектра, легко вычислить постоянную Стефана-Больцмана:
Площадь нити исследуемой лампы накаливания S =0.317·10 -3м2. Коэффициент αТ = 0.25.
|
|||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 902; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.17.137 (0.007 с.) |

 (3)
(3)
 (4),
(4), .
. (5)
(5)
 (6)
(6) (7)
(7)
 (8).
(8). (9)
(9) (10)
(10) (12)
(12) (13)
(13) (14)
(14) (15)
(15)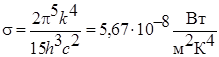 (16)
(16) (17)
(17) (18)
(18) (19)
(19) (23)
(23)


