Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ:  Археология Биология Генетика География Информатика История Логика Маркетинг Математика Менеджмент Механика Педагогика Религия Социология Технологии Физика Философия Финансы Химия ЭкологияТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Лабораторная работа №1 (УВП)Содержание книги
Поиск на нашем сайте
Лабораторная работа №1 (УВП) Тема: «Приближенное вычисление функции» Вариант 1 1. С точностью eps =0,001 подсчитать значение Sn функции F(x), представленной разложением в ряд S=S(x):
Результат сравнить со значением функции Вычисления произвести в диапазоне изменения аргумента x:
Лабораторная работа №1 (УВП) Тема: «Приближенное вычисление функции» Вариант 2 1. С точностью eps =0,001 подсчитать значение Sn функции F(x), представленной разложением в ряд S=S(x):
Результат сравнить со значением функции Вычисления произвести в диапазоне изменения аргумента x:
Лабораторная работа №1 (УВП) Тема: «Приближенное вычисление функции» Вариант 3 1. С точностью eps =0,001 подсчитать значение Sn функции F(x), представленной разложением в ряд S=S(x):
Результат сравнить со значением функции Вычисления произвести в диапазоне изменения аргумента x:
Лабораторная работа №1 (УВП) Тема: «Приближенное вычисление функции» Вариант 4 1. С точностью eps =0,001 подсчитать значение Sn функции F(x), представленной разложением в ряд S=S(x):
Результат сравнить со значением функции Вычисления произвести в диапазоне изменения аргумента x:
Лабораторная работа №1 (УВП) Тема: «Приближенное вычисление функции» Вариант 5
1. С точностью eps =0,001 подсчитать значение Sn функции F(x), представленной разложением в ряд S=S(x):
Результат сравнить со значением функции Вычисления произвести в диапазоне изменения аргумента x:
Лабораторная работа №1 (УВП) Тема: «Приближенное вычисление функции» Вариант 6 1. С точностью eps =0,001 подсчитать значение Sn функции F(x), представленной разложением в ряд S=S(x):
Результат сравнить со значением функции Вычисления произвести в диапазоне изменения аргумента x:
Лабораторная работа №1 (УВП) Тема: «Приближенное вычисление функции» Вариант 7 1. С точностью eps =0,001 подсчитать значение Sn функции F(x), представленной разложением в ряд S=S(x):
Результат сравнить со значением функции Вычисления произвести в диапазоне изменения аргумента x:
Лабораторная работа №1 (УВП) Тема: «Приближенное вычисление функции» Вариант 8 1. С точностью eps =0,001 подсчитать значение Sn функции F(x), представленной разложением в ряд S=S(x):
Результат сравнить со значением функции Вычисления произвести в диапазоне изменения аргумента x:
Вариант 9 1. С точностью eps =0,001 подсчитать значение Sn функции F(x), представленной разложением в ряд S=S(x):
Результат сравнить со значением функции Вычисления произвести в диапазоне изменения аргумента x:
Вариант 10 1. С точностью eps =0,001 подсчитать значение Sn функции F(x), представленной разложением в ряд S=S(x):
Результат сравнить со значением функции Вычисления произвести в диапазоне изменения аргумента x:
Вариант 11 1. С точностью eps =0,001 подсчитать значение Sn функции F(x), представленной разложением в ряд S=S(x):
Результат сравнить со значением функции Вычисления произвести в диапазоне изменения аргумента x:
Вариант 12 1. С точностью eps =0,001 подсчитать значение Sn функции F(x), представленной разложением в ряд S=S(x):
Результат сравнить со значением функции Вычисления произвести в диапазоне изменения аргумента x:
Вариант 13 1. С точностью eps =0,001 подсчитать значение Sn функции F(x), представленной разложением в ряд S=S(x):
Результат сравнить со значением функции Вычисления произвести в диапазоне изменения аргумента x:
Вариант 14 1. С точностью eps =0,001 подсчитать значение Sn функции F(x), представленной разложением в ряд S=S(x):
Результат сравнить со значением функции Вычисления произвести в диапазоне изменения аргумента x:
Вариант 15 1. С точностью eps =0,001 подсчитать значение Sn функции F(x), представленной разложением в ряд S=S(x):
Результат сравнить со значением функции Вычисления произвести в диапазоне изменения аргумента x:
Вариант 16 1. С точностью eps =0,001 подсчитать значение Sn функции F(x), представленной разложением в ряд S=S(x):
Результат сравнить со значением функции Вычисления произвести в диапазоне изменения аргумента x:
Вариант 17 1. С точностью eps =0,001 подсчитать значение Sn функции F(x), представленной разложением в ряд S=S(x):
Результат сравнить со значением функции Вычисления произвести в диапазоне изменения аргумента x:
Вариант 18 1. С точностью eps =0,001 подсчитать значение Sn функции F(x), представленной разложением в ряд S=S(x):
Результат сравнить со значением функции Вычисления произвести в диапазоне изменения аргумента x:
Вариант 19 1. С точностью eps =0,001 подсчитать значение Sn функции F(x), представленной разложением в ряд S=S(x):
Результат сравнить со значением функции Вычисления произвести в диапазоне изменения аргумента x:
Вариант 20 1. С точностью eps =0,001 подсчитать значение Sn функции F(x), представленной разложением в ряд S=S(x):
Результат сравнить со значением функции Вычисления произвести в диапазоне изменения аргумента x:
Вариант 21 1. С точностью eps =0,001 подсчитать значение Sn функции F(x), представленной разложением в ряд S=S(x):
Результат сравнить со значением функции Вычисления произвести в диапазоне изменения аргумента x:
Вариант 22 1. С точностью eps =0,001 подсчитать значение Sn функции F(x), представленной разложением в ряд S=S(x):
Результат сравнить со значением функции
Вычисления произвести в диапазоне изменения аргумента x:
Вариант 23 1. С точностью eps =0,001 подсчитать значение Sn функции F(x), представленной разложением в ряд S=S(x):
Результат сравнить со значением функции Вычисления произвести в диапазоне изменения аргумента x:
Вариант 24 1. С точностью eps =0,001 подсчитать значение Sn функции F(x), представленной разложением в ряд S=S(x):
Результат сравнить со значением функции Вычисления произвести в диапазоне изменения аргумента x:
Вариант 25 1. С точностью eps =0,001 подсчитать значение Sn функции F(x), представленной разложением в ряд S=S(x):
Результат сравнить со значением функции Вычисления произвести в диапазоне изменения аргумента x:
Вариант 26 1. С точностью eps =0,001 подсчитать значение Sn функции F(x), представленной разложением в ряд S=S(x):
Результат сравнить со значением функции Вычисления произвести в диапазоне изменения аргумента x:
Вариант 27 1. С точностью eps =0,001 подсчитать значение Sn функции F(x), представленной разложением в ряд S=S(x):
Результат сравнить со значением функции Вычисления произвести в диапазоне изменения аргумента x:
Вариант 28 1. С точностью eps =0,001 подсчитать значение Sn функции F(x), представленной разложением в ряд S=S(x):
Результат сравнить со значением функции Вычисления произвести в диапазоне изменения аргумента x:
Вариант 29
1. С точностью eps =0,001 подсчитать значение Sn функции F(x), представленной разложением в ряд S=S(x):
Результат сравнить со значением функции Вычисления произвести в диапазоне изменения аргумента x:
Вариант 30 1. С точностью eps =0,001 подсчитать значение Sn функции F(x), представленной разложением в ряд S=S(x):
Результат сравнить со значением функции Вычисления произвести в диапазоне изменения аргумента x: 0.1£ x £0.6 с заданным шагом h=(b-a)/k, k =10. Составить программу используя операторы While и Repeat. На печать выдавать в виде таблицы: аргумент x, значения S и f, количество членов ряда n, обеспечивающих заданную точность и значения n -го члена ряда.
Вариант 31 1. С точностью eps =0,001 подсчитать значение Sn функции F(x), представленной разложением в ряд S=S(x):
Результат сравнить со значением функции Вычисления произвести в диапазоне изменения аргумента x: 0.2£ x £0.8 с заданным шагом h=(b-a)/k, k =10. Составить программу используя операторы While и Repeat. На печать выдавать в виде таблицы: аргумент x, значения S и f, количество членов ряда n, обеспечивающих заданную точность и значения n -го члена ряда. Вариант 32 1. С точностью eps =0,001 подсчитать значение Sn функции F(x), представленной разложением в ряд S=S(x):
Результат сравнить со значением функции Вычисления произвести в диапазоне изменения аргумента x: 0.1£ x £0.8 с заданным шагом h=(b-a)/k, k =10. Составить программу используя операторы While и Repeat. На печать выдавать в виде таблицы: аргумент x, значения S и f, количество членов ряда n, обеспечивающих заданную точность и значения n -го члена ряда. Вариант 33 1. С точностью eps =0,001 подсчитать значение Sn функции F(x), представленной разложением в ряд S=S(x):
Результат сравнить со значением функции Вычисления произвести в диапазоне изменения аргумента x: 0.1£ x £0.8 с заданным шагом h=(b-a)/k, k =10. Составить программу используя операторы While и Repeat. На печать выдавать в виде таблицы: аргумент x, значения S и f, количество членов ряда n, обеспечивающих заданную точность и значения n -го члена ряда. Вопросы: 1. Суммирование элементов ряда. 2. Операторы цикла: While, Repeat, for. 3. Процедуры управления работой циклов (continue, break).
Лабораторная работа №1 (УВП)
|
|||||||||
|
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 206; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.26.47 (0.006 с.) |
.
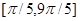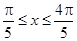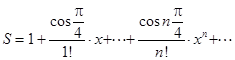
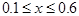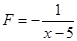с заданным шагом h=(b-a)/k, k =10. Составить программу используя операторы While и Repeat. На печать выдавать в виде таблицы: аргумент x, значения S и f, количество членов ряда n, обеспечивающих заданную точность и значения n -го члена ряда.
.
с заданным шагом h=(b-a)/k, k =10. Составить программу используя операторы While и Repeat. На печать выдавать в виде таблицы: аргумент x, значения S и f, количество членов ряда n, обеспечивающих заданную точность и значения n -го члена ряда.
.
.
.
с заданным шагом h=(b-a)/k, k =10. Составить программу используя операторы While и Repeat. На печать выдавать в виде таблицы: аргумент x, значения S и f, количество членов ряда n, обеспечивающих заданную точность и значения n -го члена ряда.
.
.
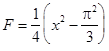с заданным шагом h=(b-a)/k, k =10. Составить программу используя операторы While и Repeat. На печать выдавать в виде таблицы: аргумент x, значения S и f, количество членов ряда n, обеспечивающих заданную точность и значения n -го члена ряда.
.
.
с заданным шагом h=(b-a)/k, k =10. Составить программу используя операторы While и Repeat. На печать выдавать в виде таблицы: аргумент x, значения S и f, количество членов ряда n, обеспечивающих заданную точность и значения n -го члена ряда.
.
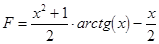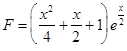с заданным шагом h=(b-a)/k, k =10. Составить программу используя операторы While и Repeat. На печать выдавать в виде таблицы: аргумент x, значения S и f, количество членов ряда n, обеспечивающих заданную точность и значения n -го члена ряда.
.
.
с заданным шагом h=(b-a)/k, k =10. Составить программу используя операторы While и Repeat. На печать выдавать в виде таблицы: аргумент x, значения S и f, количество членов ряда n, обеспечивающих заданную точность и значения n -го члена ряда.
.
.
.
.
.
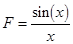с заданным шагом h=(b-a)/k, k =10. Составить программу используя операторы While и Repeat. На печать выдавать в виде таблицы: аргумент x, значения S и f, количество членов ряда n, обеспечивающих заданную точность и значения n -го члена ряда.
.
с заданным шагом h=(b-a)/k, k =10. Составить программу используя операторы While и Repeat. На печать выдавать в виде таблицы: аргумент x, значения S и f, количество членов ряда n, обеспечивающих заданную точность и значения n -го члена ряда.
.
.
.
.
.
.
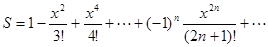
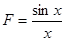с заданным шагом h=(b-a)/k, k =10. Составить программу используя операторы While и Repeat. На печать выдавать в виде таблицы: аргумент x, значения S и f, количество членов ряда n, обеспечивающих заданную точность и значения n -го члена ряда.
.
.
с заданным шагом h=(b-a)/k, k =10. Составить программу используя операторы While и Repeat. На печать выдавать в виде таблицы: аргумент x, значения S и f, количество членов ряда n, обеспечивающих заданную точность и значения n -го члена ряда.
.
.
с заданным шагом h=(b-a)/k, k =10. Составить программу используя операторы While и Repeat. На печать выдавать в виде таблицы: аргумент x, значения S и f, количество членов ряда n, обеспечивающих заданную точность и значения n -го члена ряда.
.
с заданным шагом h=(b-a)/k, k =10. Составить программу используя операторы While и Repeat. На печать выдавать в виде таблицы: аргумент x, значения S и f, количество членов ряда n, обеспечивающих заданную точность и значения n -го члена ряда.
.
.
.
.
.
