Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Plot(xx,v,'ob','MarkerSize',5,'LineWidth',2) ⇐ ПредыдущаяСтр 2 из 2
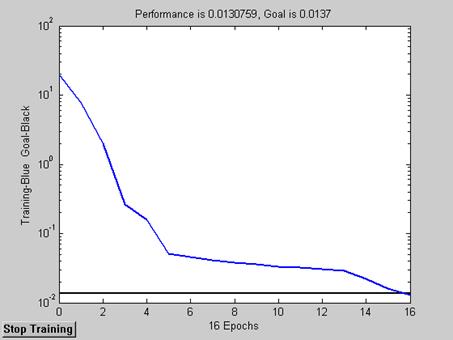
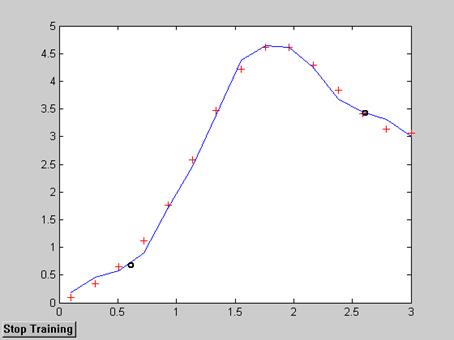
В результате выполнения программы получаются следующие результаты, отражённые на рис. 3 и 4:
В массиве v содержатся приближённые значения для двух контрольных точек, указанных на графике (рис. 2) xx=[0.61 2.61]. При данных параметрах сети получены значения: v = [1.05 3.35]. Сравнив эти приближённые значения с точными значениями [0.85 3.37], можно сделать вывод о корректности построения нейронной сети.
Отчёт о выполнении работы Отчёт о выполнении лабораторной работы №1 должен быть выполнен на листах формата А4 и содержать следующие результаты: 1. Исходные данные (рис. 2); 2. Текст программы с подробными комментариями; 3. Характеристику точности обучения (рис. 3); 4. Результаты моделирования (рис. 4); 5. Сопоставление результатов в контрольных точках; 6. Краткие выводы о результатах работы.
Лабораторная работа № 2 Аппроксимация функции двух переменных Цель работы Научиться работать с радиальной базисной сетью, функции newrbe и newrb.
Краткие теоретические сведения Радиальные базисные сети предназначены для аппроксимации функций. Возьмем произвольную непрерывную функцию и представим ее с помощью суммы колоколообразных функций. Аналитически это означает представление f (x) в виде разложения по стандартному набору пространственно локализованных функций:
где
Функция newrbe формирует радиальную базисную сеть с нулевой ошибкой. Сеть с радиальными базисными функциями представляет собой, как правило, сеть с тремя слоями: обычным входным слоем, скрытым радиальным базисным слоем и выходным линейным слоем. Функция newrb формирует радиальную базисную сеть с ненулевой ошибкой в отличие от newrbe. На рис. 5 показана архитектура радиальной базисной сети.
Пример решения типовой задачи
Пусть функция
x1=-1.0; x2=+1.0; y1=-1.5; y2=+1.5; nx=7; ny=9; step_x=(x2-x1)/(nx-1); step_y=(y2-y1)/(ny-1); step_min = min(step_x,step_y); [x,y]=meshgrid([x1:step_x:x2], [y1:step_y:y2]); z=exp(-x.^2).*exp(-y.^2); surf(x,y,z), title('PS. Press<enter>'); pause; xx=reshape(x,1,nx*ny); yy=reshape(y,1,nx*ny); zz=exp(-xx.^2).*exp(-yy.^2); p=[xx; yy]; t=zz; goal = 0.0371; spread = 1.0*step_min; net = newrb(p,t, goal,spread); net.layers{1}.size smlt=sim(net,p); [zz' smlt'] smltr=reshape(smlt,ny,nx); surf(x,y,smltr), title('AS. Press<enter>');
Рис. 6 иллюстрирует график исходной функции
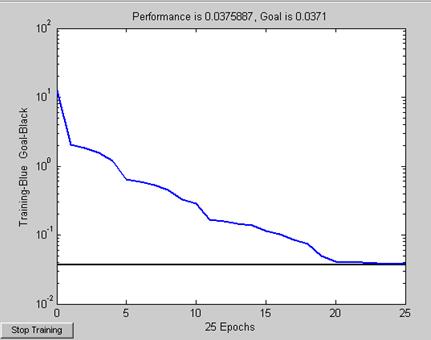
На рис. 7 показана характеристика точности обучения радиальной базисной сети и допустимая среднеквадратичная ошибка сети Goal=0.0371.
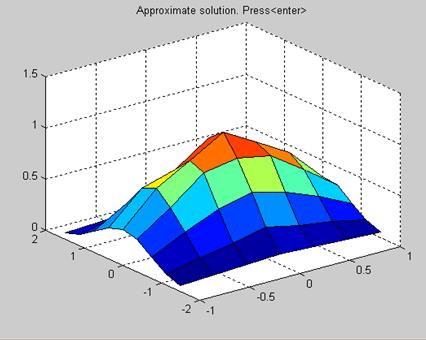
На рис. 8 отображён результат аппроксимации нелинейной зависимости, построенный с помощью радиальной базисной функции.
Сопоставляя рис. 6 и рис. 8, можно сделать вывод об удовлетворительности полученных результатов. Лучших результатов можно добиться, варьируя параметры goal и spread.
Отчёт о выполнении работы Отчёт о выполнении лабораторной работы №2 должен быть выполнен на листах формата А4 и содержать следующие результаты: 1. Исходные данные – выбор функции двух переменных и области определения функции, построение графика функции (рис. 6); 2. Текст программы с подробными комментариями; 3. Результаты моделирования (рис. 7, 8); 4. Контрольный пример; 5. Объяснение результатов проделанной работы.
Лабораторная работа № 3 Сеть Кохонена, самоорганизующаяся нейронная сеть Цель работы Изучить функционирование и процедуру обучения сети Кохонена с помощью функции newc.
|
|||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 271; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.195.110 (0.012 с.) |
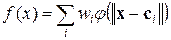 , (1)
, (1) - веса суммирования отдельных откликов,
- веса суммирования отдельных откликов, 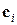 - центры базисных радиальных функций. Это формула нейронной сети на основе радиальной базисной функции. Расстояние
- центры базисных радиальных функций. Это формула нейронной сети на основе радиальной базисной функции. Расстояние  определяется как расстояние в евклидовом пространстве:
определяется как расстояние в евклидовом пространстве: . (2)
. (2)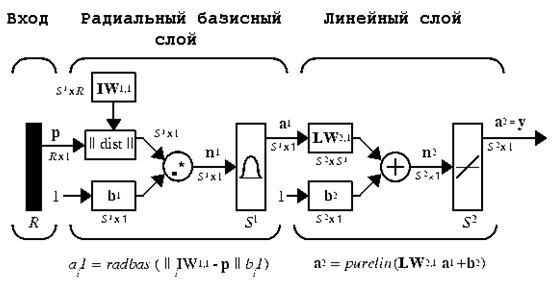
 задана на промежутках
задана на промежутках 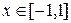 ,
,  ; количество точек разбиений по
; количество точек разбиений по  есть nx, а по
есть nx, а по 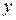 ‑ ny. Тогда, используя следующий алгоритм построения радиальной базисной сети, можно построить график функции
‑ ny. Тогда, используя следующий алгоритм построения радиальной базисной сети, можно построить график функции  :
: