
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Нахождение площади геометрической фигуры методом Монте-КарлоСодержание книги
Поиск на нашем сайте
Для определения площади под графиком функции можно использовать следующий стахостический алгоритм: 1.Ограничить функцию прямоугольником, S(пр) которого легко вычислить 2.Набросаем в этом прямоугольнике некоторое количество точек, координаты которых будем выбирать случайным образом.(n-шт.) 3.Определим число точек, которые попадут под график функции.(k-шт.) 4.S области, ограниченной функцией и осями координат даѐтся выражением S=S(пр)k\n. Для малого числа измерений интегрированной функции производительность Монте-Карло интегрирования ниже, чем производительность простого метода вычисления. В случаях, когда функция задана неявно стахостичекий метод оказывается более продуктивным.
называется матрицей смежностей графа G = (V, E). Ребра графа могут быть ориентированными или неориентированными. При изучении бинарных отношений были использованы графы, все ребра которых ориентированы. Такие графы называют ориентированными графами или орграфами. Если вершины vi и vj (i≠j) соединены ребром ek= (vi,vj), то их называют смежными вершинами. Если ребра ek, el имеют общую вершину, то их называют смежными ребрами. Если вершина vi является концом ребра ej, то vi называют вершиной, инцидентной ребру ej, а ej – ребром, инцидентным вершине vi. Степенью вершины графа называется число инцидентных ей ребер, (число вершин смежных этой вершине, число ребер выходящих из этой вершины, число ребер входящих в нее). Обозначают степень вершины v через deg (v). Вершина называется изолированной, если еѐ степень равна нулю, и называется концевой (висячей), если еѐ степень равна единице. Вершина называется доминирующей, если она смежная со всеми вершинами графа. Сумма степеней всех вершин графа есть четное число. в любом графе число вершин с нечетными степенями четно.
17. Способы задания графа. Матрицы смежностей и инциденций. Обходы графов Фиксируем на плоскости произвольным образом п точек и произвольным образом дадим им в качестве имен имена вершин данного графа. В итоге на плоскости возникнут точки, обозначенные как
Число вершин графа называют порядком графа и обозначают / V / = n. Граф будем обозначать парой G = (V, E). Граф G называется помеченным, если его вершинам приписаны числа 1, 2, …, n, где n − порядок графа.
В приведенном выше примере графа матрица смежностей такова:
Во многих задачах, решаемых с использованием графов, требуется проложить маршрут от одной вершины графа к другой или обойти все его вершины, учитывая те или иные ограничения. Маршрут – это последовательность вершин и ребер графа, следуя по которым, можно попасть из одной его вершины в другую. Цепь – это маршрут без повторяющихся ребер. Путь – это цепь, все вершины которой (за исключением, быть может, начальной и конечной) различны. Цикл – это цепь, у которой совпадают начальная и конечная вершины, а все остальные различны Граф называют связным, если из каждой его вершины существует путь в любую другую его вершину. Граф, рассмотренный в примере, является, связным. Если удалить из него ребро, то он потеряет связность и распадется на компоненты: одна из компонент будет содержать вершину Д и петлю, вторая компонента – вершины А,В,С,Е, связанные между собой всеми оставшимися ребрами. Для представления данных в алгоритмах на дискретных структурах часто используются графы, которые называются деревьями. Деревом называют связный неорграф, не содержащий циклов. Если граф связный, но не является деревом, в нем всегда можно выделить часть, включающую все вершины и образующую дерево. Такую часть графа называют остовом графа. Если граф несвязен, то можно превратить в дерево каждую его компоненту. Полученная совокупность деревьев носит название остовного леса. Остовным деревом связного графа G называется любой его подграф, содержащий все вершины графа G и являющийся деревом.
|
|||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 969; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.68 (0.009 с.) |




 . Затем для каждой пары точек
. Затем для каждой пары точек  таких, что
таких, что 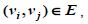 , проведем отрезок прямой, соединяющий точки
, проведем отрезок прямой, соединяющий точки 


 В каждом столбце матрицы инциденций всегда ровно две единицы, остальные элементы равны нулю. Если в графе все вершины имеют степень ноль, то матрицы инциденций - нулевая.
В каждом столбце матрицы инциденций всегда ровно две единицы, остальные элементы равны нулю. Если в графе все вершины имеют степень ноль, то матрицы инциденций - нулевая.


