
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Логика построения шифра и структура ключевой информации госта.Содержание книги
Поиск на нашем сайте
Содержание Вместо предисловия...................................................................................................................... 2 1. Описание алгоритма................................................................................................................. 1.1. Термины и обозначения..................................................................................................... 1.2. Логика построения шифра и структура ключевой информации ГОСТа..................... 1.3. Основной шаг криптопреобразования............................................................................. 1.4. Базовые циклы криптографических преобразований.................................................... 1.5. Основные режимы шифрования....................................................................................... 2. Обсуждение криптографических алгоритмов ГОСТа........................................................ 2.1. Криптографическая стойкость ГОСТа........................................................................... 2.2. Замечания по архитектуре ГОСТа.................................................................................. 2.3. Требования к качеству ключевой информации и источники ключей....................... 3. Замечания по реализации....................................................................................................... 3.1. Три шага оптимизации.................................................................................................... 3.2. Описание функций и особенности реализации............................................................ 3.3. Вопрос быстродействия................................................................................................... 4. Вопросы использования стандарта....................................................................................... 4.1. Надежность реализации................................................................................................... 4.2. Вариации на тему ГОСТа................................................................................................ 4.3. Необычная работа криптографической гаммы.............................................................
То, что информация имеет ценность, люди осознали очень давно – недаром переписка сильных мира сего издавна была объектом пристального внимания их недругов и друзей. Тогда-то и возникла задача защиты этой переписки от чрезмерно любопытных глаз. Древние пытались использовать для решения этой задачи самые разнообразные методы, и одним из них была тайнопись – умение составлять сообщения таким образом, чтобы его смысл был недоступен никому кроме посвященных в тайну. Есть свидетельства тому, что искусство тайнописи зародилось еще в доантичные времена. На протяжении всей своей многовековой истории, вплоть до совсем недавнего времени, это искусство служило немногим, в основном верхушке общества, не выходя за пределы резиденций глав государств, посольств и – конечно же! – разведывательных миссий. И лишь несколько десятилетий назад все изменилось коренным образом – информация приобрела самостоятельную коммерческую ценность и стала широко распространенным, почти обычным товаром. Ее производят, хранят, транспортируют, продают и покупают, а значит – воруют и подделывают – и, следовательно, ее необходимо защищать. Современное общество все в большей степени становится информационно–обусловленным, успех любого вида деятельности все сильней зависит от обладания определенными сведениями и от отсутствия их у конкурентов. И чем сильней проявляется указанный эффект, тем больше потенциальные убытки от злоупотреблений в информационной сфере, и тем больше потребность в защите информации. Одним словом, возникновение индустрии обработки информации с железной необходимостью привело к возникновению индустрии средств защиты информации.
Среди всего спектра методов защиты данных от нежелательного доступа особое место занимают криптографические методы. В отличие от других методов, они опираются лишь на свойства самой информации и не используют свойства ее материальных носителей, особенности узлов ее обработки, передачи и хранения. Образно говоря, криптографические методы строят барьер между защищаемой информацией и реальным или потенциальным злоумышленником из самой информации. Конечно, под криптографической защитой в первую очередь – так уж сложилось исторически – подразумевается шифрование данных. Раньше, когда эта операция выполнялось человеком вручную или с использованием различных приспособлений, и при посольствах содержались многолюдные отделы шифровальщиков, развитие криптографии сдерживалось проблемой реализации шифров, ведь придумать можно было все что угодно, но как это реализовать… Появление цифровых электронно-вычислительных машин, приведшее в конечном итоге к созданию мощной информационной индустрии, изменило все коренным образом и в этой сфере. С одной стороны, взломщики шифров получили в свои руки чрезвычайно мощное орудие, с другой стороны, барьер сложности реализации исчез и для создателей шифров открылись практически безграничные перспективы. Все это определило стремительный прогресс криптографии в последние десятилетия.
Как всякое уважающее себя государство, Российская Федерация имеет свой стандарт шифрования. Этот стандарт закреплен ГОСТом №28147-89, принятом, как явствует из его обозначения, еще в 1989 году в СССР. Однако, без сомнения, история этого шифра гораздо более давняя. Стандарт родился предположительно в недрах восьмого главного управления КГБ СССР, преобразованного ныне в ФАПСИ. Мне довелось беседовать с людьми, утверждавшими, что еще в 70-х годах они участвовали в проектах создания программных и аппаратных реализаций этого шифра для различных компьютерных платформ. В те времена он имел гриф «Сов. секретно», позже гриф был изменен на «секретно», затем снят совсем. На моем экземпляре ГОСТа стояла лишь скромная пометка «ДСП». К сожалению, в отличие от самого стандарта, история его создания и критерии проектирования шифра до сих пор остаются тайной за семью печатями. Возможное использование ГОСТа в Ваших собственных разработках ставит ряд вопросов. Вопрос первый – нет ли юридических препятствий для этого. Ответ здесь простой – таких препятствий нет и вы можете свободно использовать ГОСТ, он не запатентован, следовательно, не у кого спрашивать разрешения. Более того, вы имеете на это полное моральное право как наследники тех, кто оплатил разработку стандарта из своего кармана, – прежде всего я имею ввиду ваших родителей. Известный указ Президента России №334 от 03.04.95 и соответствующие постановления правительства ничего нового не вносят в эту картину. Хотя они формально и запрещают разработку систем, содержащих средства криптозащиты юридическими и физическими лицами, не имеющими лицензии на этот вид деятельности, но реально указ распространяется лишь на случай государственных секретов, данных, составляющих банковскую тайну и т.п., словом, он действует только там, где нужна бумажка, что «данные защищены». Хорошо, с правомочностью применения ГОСТа разобрались, теперь остановимся на вопросе целесообразности – прежде всего, можем ли мы доверять этому порождению мрачной Лубянки, не встроили ли товарищи чекисты лазеек в алгоритмы шифрования? Это весьма маловероятно, так как ГОСТ создавался в те времена, когда было немыслимо его использование за пределами государственных режимных объектов. С другой стороны, стойкость криптографического алгоритма нельзя подтвердить, ее можно только опровергнуть взломом. Поэтому, чем старше алгоритм, тем больше шансов на то, что, если уж он не взломан до сих пор, он не будет взломан и в ближайшем обозримом будущем. В этом свете все разговоры о последних «оригинальных разработках» «талантливых ребят» в принципе не могут быть серьезными – каждый шифр должен выдержать проверку временем. Но ведь шифров, выдержавших подобную проверку, заведомо больше одного – кроме ГОСТа ведь есть еще и DES, его старший американский братец, есть и другие шифры. Почему тогда ГОСТ? Конечно, во многом это дело личных пристрастий, но надо помнить еще и о том, что ГОСТ по большинству параметров превосходит все эти алгоритмы, в том числе и DES. И, в конце концов, где же наш Российский Патриотизм?! Широкому использованию ГОСТа в разработках Российских программистов мешает, по моему мнению, недостаток опубликованной информации о нем, а также некий ореол таинственности, сложившийся вокруг него и искусно кем-то поддерживаемый. На самом деле ничего сложного в шифре нет, он доступен для понимания и реализации программисту любого уровня, но, как и во всем прочем, для создания действительно хорошей реализации надо быть профессионалом. Я работал с ГОСТом как программист с 91 по 94 год, и за это время у меня получилась весьма удачная (ну как себя не похвалить!) его программная реализация для процессоров семейства Intel x86, приближающаяся по быстродействию к возможному оптимуму.
Целью настоящей статьи является знакомство всех заинтересованных с самим алгоритмом и его реализацией на платформе Intel x86. Разработанную мной реализацию ГОСТа я предоставляю в общественную собственность, ее может использовать каждый при условии ссылки на мое авторство. Текст настоящей статьи может неограниченно распространяться в печатном и электронном виде в том и только в том случае, если это не сопряжено прямо или косвенно с извлечением прибыли, в противном случае требуется мое письменное разрешение. Статья состоит из четырех частей. Первая часть содержит описание, а вторая – обсуждение алгоритма, третья и четвертая части содержат соответственно описание его реализации и обсуждение некоторых аспектов его применения. Итак, начнем... Описание алгоритма. Термины и обозначения. Описание стандарта шифрования Российской Федерации содержится в очень интересном документе, озаглавленном «Алгоритм криптографического преобразования данных ГОСТ 28147-89». То, что в его названии вместо термина «шифрование» фигурирует более общее понятие «криптографическое преобразование», вовсе не случайно. Помимо нескольких тесно связанных между собой процедур шифрования, в документе описан один построенный на общих принципах с ними алгоритм выработки имитовставки. Последняя является не чем иным, как криптографической контрольной комбинацией, то есть кодом, вырабатываемым из исходных данных с использованием секретного ключа с целью имитозащиты, или защиты данных от внесения в них несанкционированных изменений. На различных шагах алгоритмов ГОСТа данные, которыми они оперируют, интерпретируются и используются различным образом. В некоторых случаях элементы данных обрабатываются как массивы независимых битов, в других случаях – как целое число без знака, в третьих – как имеющий структуру сложный элемент, состоящий из нескольких более простых элементов. Поэтому во избежание путаницы следует договориться об используемых обозначениях.
Элементы данных в данной статье обозначаются заглавными латинскими буквами с наклонным начертанием (например, X). Через | X | обозначается размер элемента данных X в битах. Таким образом, если интерпретировать элемент данных X как целое неотрицательное число, можно записать следующее неравенство: 0£ X <2| X |. Если элемент данных состоит из нескольких элементов меньшего размера, то этот факт обозначается следующим образом: X = (X 0, X 1,..., X n -1) = X 0|| X 1||...|| X n -1. Процедура объединения нескольких элементов данных в один называется конкатенацией данных и обозначается символом ||. Естественно, для размеров элементов данных должно выполняться следующее соотношение: | X |=| X 0|+| X 1|+...+| X n -1|. При задании сложных элементов данных и операции конкатенации составляющие элементы данных перечисляются в порядке возрастания старшинства. Иными словами, если интерпретировать составной элемент и все входящие в него элементы данных как целые числа без знака, то можно записать следующее равенство:
В алгоритме элемент данных может интерпретироваться как массив отдельных битов, в этом случае биты обозначаем той же самой буквой, что и массив, но в строчном варианте, как показано на следующем примере: X = (x 0, x 1,..., x n –1) = x 0+21· x 1+...+2 n –1· xn –1. Если над элементами данных выполняется некоторая операция, имеющая логический смысл, то предполагается, что данная операция выполняется над соответствующими битами элементов. Иными словами A • B =(a 0• b 0, a 1• b 1,..., a n -1• b n -1), где n =| A |=| B |, а символом “•” обозначается произвольная бинарная логическая операция; как правило, имеется ввиду операция исключающего или, она же – операция суммирования по модулю 2: a Å b = (a + b) mod 2. Основные режимы шифрования. ГОСТ 28147-89 предусматривает три следующих режима шифрования данных: · простая замена, · гаммирование, · гаммирование с обратной связью, и один дополнительный режим выработки имитовставки. В любом из этих режимов данные обрабатываются блоками по 64 бита, на которые разбивается массив, подвергаемый криптографическому преобразованию, именно поэтому ГОСТ относится к блочным шифрам. Однако в двух режимах гаммирования есть возможность обработки неполного блока данных размером меньше 8 байт, что существенно при шифровании массивов данных с произвольным размером, который может быть не кратным 8 байтам. Прежде чем перейти к рассмотрению конкретных алгоритмов криптографических преобразований, необходимо пояснить обозначения, используемые на схемах в следующих разделах: T о, T ш – массивы соответственно открытых и зашифрованных данных;
n – число 64-битных блоков в массиве данных; Ц X – функция преобразования 64-битного блока данных по алгоритму базового цикла «X»; Теперь опишем основные режимы шифрования:
Простая замена. Зашифрование в данном режиме заключается в применении цикла 32-З к блокам открытых данных, расшифрование – цикла 32-Р к блокам зашифрованных данных. Это наиболее простой из режимов, 64-битовые блоки данных обрабатываются в нем независимо друг от друга. Схемы алгоритмов зашифрования и расшифрования в режиме простой замены приведены на рисунках 3а и б соответственно, они тривиальны и не нуждаются в комментариях. Размер массива открытых или зашифрованных данных, подвергающийся соответственно зашифрованию или расшифрованию, должен быть кратен 64 битам: | T о | = | T ш | =64· n, после выполнения операции размер полученного массива данных не изменяется.
Режим шифрования простой заменой имеет следующие особенности: 1. Так как блоки данных шифруются независимо друг от друга и от их позиции в массиве, при зашифровании двух одинаковых блоков открытого текста получаются одинаковые блоки шифротекста и наоборот. Отмеченное свойство позволит криптоаналитику сделать заключение о тождественности блоков исходных данных, если в массиве зашифрованных данных ему встретились идентичные блоки, что является недопустимым для серьезного шифра. 2. Если длина шифруемого массива данных не кратна 8 байтам или 64 битам, возникает проблема, чем и как дополнять последний неполный блок данных массива до полных 64 бит. Эта задача не так проста, как кажется на первый взгляд, поскольку очевидные решения типа «дополнить неполный блок нулевыми битами» или, более обще, «дополнить неполный блок фиксированной комбинацией нулевых и единичных битов» могут при определенных условиях дать в руки криптоаналитика возможность методами перебора определить содержимое этого самого неполного блока, и этот факт означает снижение стойкости шифра. Кроме того, длина шифротекста при этом изменится, увеличившись до ближайшего целого, кратного 64 битам, что часто бывает нежелательным. На первый взгляд, перечисленные выше особенности делают практически невозможным использование режима простой замены, ведь он может применяться только для шифрования массивов данных с размером кратным 64 битам, не содержащим повторяющихся 64-битных блоков. Кажется, что для любых реальных данных гарантировать выполнение указанных условий невозможно. Это почти так, но есть одно очень важное исключение: вспомните, что размер ключа составляет 32 байта, а размер таблицы замен – 64 байта. Кроме того, наличие повторяющихся 8-байтовых блоков в ключе или таблице замен будет говорить об их весьма плохом качестве, поэтому в реальных ключевых элементах такого повторения быть не может. Таким образом мы выяснили, что режим простой замены вполне подходит для шифрования ключевой информации, тем более, что прочие режимы для этой цели менее удобны, поскольку требуют наличия дополнительного синхронизирующего элемента данных – синхропосылки (см. следующий раздел). Наша догадка верна, ГОСТ предписывает использовать режим простой замены исключительно для шифрования ключевых данных. Гаммирование. Как же можно избавиться от недостатков режима простой замены? Для этого необходимо сделать возможным шифрование блоков с размером менее 64 бит и обеспечить зависимость блока шифротекста от его номера, иными словами, рандомизировать процесс шифрования. В ГОСТе это достигается двумя различными способами в двух режимах шифрования, предусматривающих гаммирование. Гаммирование – это наложение (снятие) на открытые (зашифрованные) данные криптографической гаммы, то есть последовательности элементов данных, вырабатываемых с помощью некоторого криптографического алгоритма, для получения зашифрованных (открытых) данных. Для наложения гаммы при зашифровании и ее снятия при расшифровании должны использоваться взаимно обратные бинарные операции, например, сложение и вычитание по модулю 264 для 64-битных блоков данных. В ГОСТе для этой цели используется операция побитного сложения по модулю 2, поскольку она является обратной самой себе и к тому же наиболее просто реализуется. Гаммирование решает обе упомянутые проблемы; во первых, все элементы гаммы различны для реальных шифруемых массивов и, следовательно, результат зашифрования даже двух одинаковых блоков в одном массиве данных будет различным. Во вторых, хотя элементы гаммы и вырабатываются одинаковыми порциями в 64 бита, использоваться может и часть такого блока с размером, равным размеру шифруемого блока. Теперь перейдем непосредственно к описанию режима гаммирования. Гамма для этого режима получается следующим образом: с помощью некоторого алгоритмического рекуррентного генератора последовательности чисел (РГПЧ) вырабатываются 64-битные блоки данных, которые далее подвергаются преобразованию по циклу 32-З, то есть зашифрованию в режиме простой замены, в результате получаются блоки гаммы. Благодаря тому, что наложение и снятие гаммы осуществляется при помощи одной и той же операции побитового исключающего или, алгоритмы зашифрования и расшифрования в режиме гаммирования идентичны, их общая схема приведена на рисунке 5. РГПЧ, используемый для выработки гаммы, является рекуррентной функцией: W i +1= f (W i), где W i – элементы рекуррентной последовательности, f – функция преобразования. Следовательно, неизбежно возникает вопрос о его инициализации, то есть об элементе W0. В действительности, этот элемент данных является параметром алгоритма для режимов гаммирования, на схемах он обозначен как S, и называется в криптографии синхропосылкой, а в нашем ГОСТе – начальным заполнением одного из регистров шифрователя. По определенным соображениям разработчики ГОСТа решили использовать для инициализации РГПЧ не непосредственно синхропосылку, а результат ее преобразования по циклу 32-З: W0= Ц 32-З(S). Последовательность элементов, вырабатываемых РГПЧ, целиком зависит от его начального заполнения, то есть элементы этой последовательности являются функцией своего номера и начального заполнения РГПЧ: W i = f i (W0), где f i (X)= f (f i –1(X)), f 0(X)= X. С учетом преобразования по алгоритму простой замены добавляется еще и зависимость от ключа: Г i = Ц 32-З(W i)= Ц 32-З(f i (W0))= Ц 32-З(f i (Ц 32-З(S)))=j i (S, K), где Г i – i -тый элемент гаммы, K – ключ. Таким образом, последовательность элементов гаммы для использования в режиме гаммирования однозначно определяется ключевыми данными и синхропосылкой. Естественно, для обратимости процедуры шифрования в процессах за- и расшифрования должна использоваться одна и та же синхропосылка. Из требования уникальности гаммы, невыполнение которого приводит к катастрофическому снижению стойкости шифра, следует, что для шифрования двух различных массивов данных на одном ключе необходимо обеспечить использование различных синхропосылок. Это приводит к необходимости хранить или передавать синхропосылку по каналам связи вместе с зашифрованными данными, хотя в отдельных особых случаях она может быть предопределена или вычисляться особым образом, если исключается шифрование двух массивов на одном ключе. Теперь подробно рассмотрим РГПЧ, используемый в ГОСТе для генерации элементов гаммы. Прежде всего надо отметить, что к нему не предъявляются требования обеспечения каких-либо статистических характеристик вырабатываемой последовательности чисел. РГПЧ спроектирован разработчиками ГОСТа исходя из необходимости выполнения следующих условий: · период повторения последовательности чисел, вырабатываемой РГПЧ, не должен сильно (в процентном отношении) отличаться от максимально возможного при заданном размере блока значения 264; · соседние значения, вырабатываемые РГПЧ, должны отличаться друг от друга в каждом байте, иначе задача криптоаналитика будет упрощена; · РГПЧ должен быть достаточно просто реализуем как аппаратно, так и программно на наиболее распространенных типах процессоров, большинство из которых, как известно, имеют разрядность 32 бита. Исходя из перечисленных принципов создатели ГОСТа спроектировали весьма удачный РГПЧ, имеющий следующие характеристики: · в 64-битовом блоке старшая и младшая части обрабатываются независимо друг от друга: · рекуррентные соотношения для старшей и младшей частей следующие:
Нижний индекс в записи числа означает его систему счисления, таким образом, константы, используемые на данном шаге, записаны в 16-ричной системе счисления. Второе выражение нуждается в комментариях, так как в тексте ГОСТа приведено нечто другое: · период повторения последовательности для младшей части составляет 232, для старшей части 232–1, для всей последовательности период составляет 232×(232–1), доказательство этого факта, весьма несложное, получите сами. Первая формула из двух реализуется за одну команду, вторая, несмотря на ее кажущуюся громоздкость, за две команды на всех современных 32-разрядных процессорах.
Схема алгоритма шифрования в режиме гаммирования приведена на рисунке 4, ниже изложены пояснения к схеме: Øàã 0. Определяет исходные данные для основного шага криптопреобразования: · T о(ш) – массив открытых (зашифрованных) данных произвольного размера, подвергаемый процедуре зашифрования (расшифрования), по ходу процедуры массив подвергается преобразованию порциями по 64 бита; · S – ñèíõðîïîñûëêà, 64-битный элемент данных, необходимый для инициализации генератора гаммы; Øàã 1. Начальное преобразование синхропосылки, выполняемое для ее «рандомизации», то есть для устранения статистических закономерностей, присутствующих в ней, результат используется как начальное заполнение РГПЧ; Øàã 2. Один шаг работы РГПЧ, реализующий его рекуррентный алгоритм. В ходе данного шага старшая (S 1) и младшая (S 0) части последовательности данных вырабатываются независимо друг от друга; Øàã 3. Гаммирование. Очередной 64-битный элемент, выработанный РГПЧ, подвергается процедуре зашифрования по циклу 32–З, результат используется как элемент гаммы для зашифрования (расшифрования) очередного блока открытых (зашифрованных) данных того же размера. Øàã 4. Результат работы алгоритма – зашифрованный (расшифрованный) массив данных. Ниже перечислены особенности гаммирования как режима шифрования. 1. Одинаковые блоки в открытом массиве данных дадут при зашифровании различные блоки шифротекста, что позволит скрыть факт их идентичности. 2. Поскольку наложение гаммы выполняется побитно, шифрование неполного блока данных легко выполнимо как шифрование битов этого неполного блока, для чего используется соответствующие биты блока гаммы. Так, для зашифрования неполного блока в 1 бит можно использовать любой бит из блока гаммы. 3. Синхропосылка, использованная при зашифровании, каким-то образом должна быть передана для использования при расшифровании. Это может быть достигнуто следующими путями: · хранить или передавать синхропосылку вместе с зашифрованным массивом данных, что приведет к увеличению размера массива данных при зашифровании на размер синхропосылки, то есть на 8 байт; · использовать предопределенное значение синхропосылки или вырабатывать ее синхронно источником и приемником по определенному закону, в этом случае изменение размера передаваемого или хранимого массива данных отсутствует; Оба способа дополняют друг друга, и в тех редких случаях, где не работает первый, наиболее употребительный из них, может быть использован второй, более экзотический. Второй способ имеет гораздо меньшее применение, поскольку сделать синхропосылку предопределенной можно только в том случае, если на данном комплекте ключевой информации шифруется заведомо не более одного массива данных, что бывает в редких случаях. Генерировать синхропосылку синхронно у источника и получателя массива данных также не всегда представляется возможным, поскольку требует жесткой привязки к чему-либо в системе. Так, здравая на первый взгляд идея использовать в качестве синхропосылки в системе передачи зашифрованных сообщений номер передаваемого сообщения не подходит, поскольку сообщение может потеряться и не дойти до адресата, в этом случае произойдет десинхронизация систем шифрования источника и приемника. Поэтому в рассмотренном случае нет альтернативы передаче синхропосылки вместе с зашифрованным сообщением. С другой стороны, можно привести и обратный пример. Допустим, шифрование данных используется для защиты информации на диске, и реализовано оно на низком уровне, для обеспечения независимого доступа данные шифруются по секторам. В этом случае невозможно хранить синхропосылку вместе с зашифрованными данными, поскольку размер сектора нельзя изменить, однако ее можно вычислять как некоторую функцию от номера считывающей головки диска, номера дорожки (цилиндра) и номера сектора на дорожке. В этом случае синхропосылка привязывается к положению сектора на диске, которое вряд ли может измениться без переформатирования диска, то есть без уничтожения данных на нем. Режим гаммирования имеет еще одну интересную особенность. В этом режиме биты массива данных шифруются независимо друг от друга. Таким образом, каждый бит шифротекста зависит от соответствующего бита открытого текста и, естественно, порядкового номера бита в массиве:
где Данное свойство дает злоумышленнику возможность воздействуя на биты шифротекста вносить предсказуемые и даже целенаправленные изменения в соответствующий открытый текст, получаемый после его расшифрования, не обладая при этом секретным ключом. Это иллюстрирует хорошо известный в криптологии факт, что «секретность и аутентичность суть различные свойства шифров». Иными словами, свойства шифров обеспечивать защиту от несанкционированного ознакомления с содержимым сообщения и от несанкционированного внесения изменений в сообщение являются независимыми и лишь в отдельных случаях могут пересекаться. Сказанное означает, что существуют криптографические алгоритмы, обеспечивающие определенную секретность зашифрованных данных и при этом никак не защищающие от внесения изменений и наоборот, обеспечивающие аутентичность данных и никак не ограничивающие возможность ознакомления с ними. По этой причине рассматриваемое свойство режима гаммирования не должно рассматриваться как его недостаток. Требования к качеству ключевой информации и источники ключей. Не все ключи и таблицы замен обеспечивают максимальную стойкость шифра. Для каждого алгоритма шифрования существуют свои критерии оценки ключевой информации. Так, для алгоритма DES известно существование так называемых «слабых ключей», при использовании которых связь между открытыми и зашифрованными данными не маскируется достаточным образом, и шифр сравнительно просто вскрывается. Исчерпывающий ответ на вопрос о критериях качества ключей и таблиц замен ГОСТа если и можно вообще где-либо получить, то только у разработчиков алгоритма. Соответствующие данные не были опубликованы в открытой печати. Однако согласно установленному порядку, для шифрования информации, имеющей гриф, должны быть использованы ключевые данные, полученные от уполномоченной организации. Косвенным образом это может свидетельствовать о наличии методик проверки ключевых данных на «вшивость». Сам факт существования слабых ключевых данных в Российском стандарте шифрования не вызывает сомнения. Очевидно, нулевой ключ и тривиальная таблица замен, по которой любое значение заменяется но него самого, являются слабыми, при использовании хотя бы одного из них шифр достаточно просто взламывается, каков бы ни был второй ключевой элемент. Как уже было отмечено выше, критерии оценки ключевой информации недоступны, однако на их счет все же можно высказать некоторые соображения: 1. Ключ должен являться массивом статистически независимых битов, принимающих с равной вероятностью значения 0 и 1. При этом некоторые конкретные значения ключа могут оказаться «слабыми», то есть шифр может не обеспечивать заданный уровень стойкости в случае их использования. Однако, предположительно, доля таких значений в общей массе всех возможных ключей ничтожно мала. Поэтому ключи, выработанные с помощью некоторого датчика истинно случайных чисел, будут качественными с вероятностью, отличающейся от единицы на ничтожно малую величину. Если же ключи вырабатываются с помощью генератора псевдослучайных чисел, то используемый генератор должен обеспечивать указанные выше статистические характеристики, и, кроме того, обладать высокой криптостойкостью, не меньшей, чем у самого ГОСТа. Иными словами, задача определения отсутствующих членов вырабатываемой генератором последовательности элементов не должна быть проще, чем задача вскрытия шифра. Кроме того, для отбраковки ключей с плохими статистическими характеристиками могут быть использованы различные статистические критерии. На практике обычно хватает двух критериев, – для проверки равновероятного распределения битов ключа между значениями 0 и 1 обычно используется критерий Пирсона («хи квадрат»), а для проверки независимости битов ключа – критерий серий. Об упомянутых критериях можно прочитать в учебниках или справочниках по математической статистике. 2. Таблица замен является долговременным ключевым элементом, то есть действует в течение гораздо более длительного срока, чем отдельный ключ. Предполагается, что она является общей для всех узлов шифрования в рамках одной системы криптографической защиты. Даже при нарушении конфиденциальности таблицы замен стойкость шифра остается чрезвычайно высокой и не снижается ниже допустимого предела. К качеству отдельных узлов замен можно предъявить приведенное ниже требование. Каждый узел замен может быть описан четверкой логических функций, каждая из которых имеет четыре логических аргумента. Необходимо, чтобы эти функции были достаточно сложными. Это требование сложности невозможно выразить формально, однако в качестве необходимого условия можно потребовать, чтобы соответствующие логические функции, записанные в минимальной форме (т.е. с минимально возможной длиной выражения) с использованием основных логических операций, не были короче некоторого необходимого минимума. В первом и очень грубом приближении это условие может сойти и за достаточное. Кроме того, отдельные функции в пределах всей таблицы замен должны отличаться друг от друга в достаточной степени. На практике бывает достаточно получить узлы замен как независимые случайные перестановки чисел от 0 до 15, это может быть практически реализовано, например, с помощью перемешивания колоды из шестнадцати карт, за каждой из которых закреплено одно из значений указанного диапазона. Необходимо отметить еще один интересный факт относительно таблицы замен. Для обратимости циклов шифрования 32–З и 32–Р не требуется, чтобы узлы замен были перест
|
|||||||||||
|
Последнее изменение этой страницы: 2016-04-20; просмотров: 268; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.156.17 (0.017 с.) |


 ,
,  – i -тые по порядку 64-битные блоки соответственно открытых и зашифрованных данных:
– i -тые по порядку 64-битные блоки соответственно открытых и зашифрованных данных:  ,
,  , 1£ i £ n, последний блок может быть неполным:
, 1£ i £ n, последний блок может быть неполным:  ;
;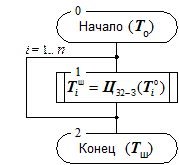 Рис. 3а. Алгоритм зашифрования данных в режиме простой замены.
Рис. 3а. Алгоритм зашифрования данных в режиме простой замены.
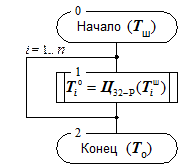 Рис. 3б. Алгоритм расшифрования данных в режиме простой замены.
Рис. 3б. Алгоритм расшифрования данных в режиме простой замены.
 , фактически, существуют два независимых РГПЧ для старшей и младшей частей блока.
, фактически, существуют два независимых РГПЧ для старшей и младшей частей блока. , где C 1=101010116;
, где C 1=101010116; , где C 2=101010416;
, где C 2=101010416; , с тем же значением константы C 2. Но далее в тексте стандарта дается комментарий, что, оказывается, под операцией взятия остатка по модулю 232–1 там понимается не то же самое, что и в математике. Отличие заключается в том, что согласно ГОСТу (232–1) mod (232–1)=(232–1), а не 0. На самом деле, это упрощает реализацию формулы, а математически корректное выражение для нее приведено выше.
, с тем же значением константы C 2. Но далее в тексте стандарта дается комментарий, что, оказывается, под операцией взятия остатка по модулю 232–1 там понимается не то же самое, что и в математике. Отличие заключается в том, что согласно ГОСТу (232–1) mod (232–1)=(232–1), а не 0. На самом деле, это упрощает реализацию формулы, а математически корректное выражение для нее приведено выше.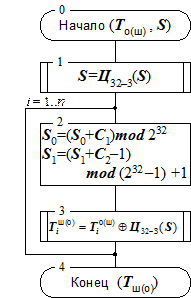 Рис. 4. Алгоритм зашифрования (расшифрования) данных в режиме гаммирования.
Рис. 4. Алгоритм зашифрования (расшифрования) данных в режиме гаммирования.
 . Из этого вытекает, что изменение бита шифротекста на противоположное значение приведет к аналогичному изменению бита открытого текста на противоположный:
. Из этого вытекает, что изменение бита шифротекста на противоположное значение приведет к аналогичному изменению бита открытого текста на противоположный: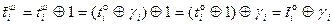 ,
, обозначает инвертированное по отношению к t значение бита (
обозначает инвертированное по отношению к t значение бита ( ).
).


