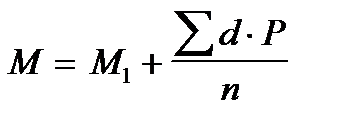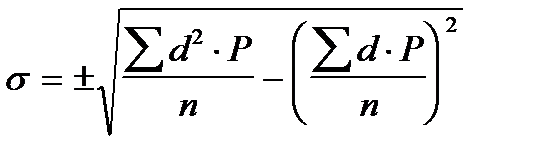Этап: Анализ (расчет показателей, изучение связей, достоверности результатов и др.) выводы и предложения.

определение цели исследования;

определение объекта наблюдения;

определение срока проведения работы на всех этапах;

указание вида статистического наблюдения и метода;

определение места, где будут проводиться наблюдения;

выяснение, какими силами и под чьим методическим и организационным руководством будут проводиться исследования.

1. Медицинская статистика, предмет изучения, основные задачи.

 

 

1. Показатели здоровья населения и методы их изучения.

Здоровье населения — здоровье людей, живущих на определенной территории.

Для оценки состояния здоровья населения используют три группы показателей:

I. Медицинские.

II. Социального благополучия — демографическая ситуация, показатели факторов окружающей среды, образ жизни, уровень медицинской помощи.

III. Психического благополучия — заболеваемость психическими расстройствами, частота невротических состояний и психопатий и др.

К медицинским показателям здоровья населения относятся: медико-демографические, заболеваемости и распространения болезней (болезненность), инвалидности и инвалидизации, физического развития населения.

К методам изучения здоровья населения относятся: медико-статистический, социологический (анкетирование, интервьюирование, посемейное комплексное обследование), экспертный, организованного эксперимента.

Индивидуальное здоровье — здоровье отдельного человека. Его оценивают по персональному самочувствию, наличию или отсутствию заболеваний, физическому состоянию и т. д.

Групповое здоровье — здоровье отдельных сообществ людей: возрастных, профессиональных и т. д.

Общественное здоровье отражает здоровье индивидуумов, из которых состоит общество, но не является суммой здоровья индивидуумов.

Потенциал общественного здоровья — мера количества и качества здоровья людей и его резервов, накопленных обществом.

Индекс общественного здоровья — соотношение здорового и нездорового образа жизни населения.

В международной практике для описания общественного здоровья традиционно используют:

1. комплекс демографических показателей: рождаемость, смертность (общую, детскую, перинатальную, младенческую, повозрастную), среднюю продолжительность предстоящей жизни;

2. показатели заболеваемости (общей, по отдельным возрастным группам, для инфекционных, хронических неспецифических заболеваний, отдельных видов заболеваний, заболеваемости с временной утратой трудоспособности и т. д.);

3. показатели инвалидности (общей, детской, повозрасной, по причинам);

4. уровень физического развития.

1. Развернутый план статистического исследования, основные положения.

 

1. Статистическое наблюдение. Ошибки статистического наблюдения.

Статистическое наблюдение - это предварительная стадия статистического исследования, которая представляет собой планомерный, научно организованный учет (сбор) первичных статистических данных о массовых социально-экономических явлениях и процессах.

Наблюдение будет статистическим, во-первых, когда оно сопровождается регистрацией изучаемых фактов в соответствующих учетных документах для дальнейшего их обобщения, во-вторых - когда носит массовый характер.

целью статистического наблюдения является получение достоверной информации о тенденциях развития явлений и процессов для последующего принятия управленческих решений.

Объект наблюдения есть некоторая исследуемая статистическая совокупность или физических лиц

Единица наблюдения - это первичный элемент объекта статистического наблюдения, который является носителем признаков, подлежащих регистрации.

Ошибки регистрации могут быть случайными и систематическими.

Случайные ошибки не имеют определенной направленности и возникают под действием случайных факторов (перестановка цифр, смещение строк и граф при заполнении статистического формуляра). При обобщении массового материала эти ошибки взаимопогашаются.

Систематические ошибки регистрации имеют определенную направленность, могут либо завышать, либо занижать конкретное значение показателя, что в итоге приводит к искажению действительного положения. Примерами систематической статистической ошибки при регистрации служат округление возраста населения на цифрах, заканчивающихся на 5 и 0

1. Статистическая группировка. Виды группировок. Основные требования к ним. Значение для качественного анализа.

Группировка - это распределение множества единиц исследуемой совокупности по группам в соответствии с существенным для данной группы признаком.

Основные виды группировок: типологические, структурные, аналитические.

Типологическая группировка – это разделение исследуемой качественно разнородной совокупности на классы, социально – экономические типы, однородные группы единиц.

Примером типологической группировки является группировка промышленных предприятий по формам собственности

Структурной называется группировка, в которой происходит разделение однородной совокупности на группы, характеризующие ее структуру по какому–либо варьирующему признаку. С помощью таких группировок может изучаться состав населения по полу, возрасту, месту проживания

Группировка, выявляющая взаимосвязи между изучаемыми явлениями и их признаками, называется аналитической группировкой

1. Статистическая обработка и сводка материала. Применение вычислительной техники в обработке статистического материала.

Статистическая обработка это систематизация первичных данных и получении на этой основе сводной характеристики всего объекта при помощи обобщающих статистических показателей.

Статистическая сводка – комплекс последовательных операций по первичной обработке данных с целью выявления типичных черт и закономерностей, присущих изучаемому явлению. Это научно-организованная обработка материалов наблюдения, включающая подсчет групповых и общих итогов, систематизацию, группировку данных и составление таблиц.

Различают простую и сложную сводку:

При простой сводке производится подсчет общих итогов по изучаемой совокупности.

При сложной сводке производится группировка единиц наблюдения, подсчет итогов по каждой группе и по всей совокупности, и представление результатов группировки в виде статистических таблиц.

Сводка состоит из следующих этапов:

-Выбор группировочного признака;

-Определение порядка формирования групп;

-Разработка системы статистических показателей для характеристики отдельных групп и совокупности в целом;

-Разработка макетов статистических таблиц для представления результатов сводки.

1. Виды статистических таблиц и правила их построения.

Статистические таблицы как средство наглядного и компактного представления цифровой информации (они бывают простыми и сложными (комбинационные и групповые)).

Простые таблицы дают количественную характеристику одного признака (например характер переломов)

Правила построения:

1. Таблица должна быть компактной и содержать только те исходные данные, которые непосредственно отражают исследуемое явление в статике и динамике и необходимы для познания его сущности.

Следует избегать ненужной, второстепенной, бессодержательной по отношению к данному объекту исследования информации. Цифровой материал необходимо излагать таким образом, чтобы при анализе таблицы сущность явления раскрывалась чтением строк слева направо и сверху вниз.

2. Заголовок таблицы и названия граф и строк должны быть четкими, краткими, лаконичными, представлять собой законченное целое, органично вписывающееся в содержание текста.

3. Информация, располагаемая в столбцах (графах) таблицы завершается итоговой строкой. Существуют различные способы соединения слагаемых граф с их итогом:

· строка "Итого" или "Всего" завершает статистическую таблицу;

4. Для того чтобы было легче читать и анализировать большие (по количеству приведенных строк) таблицы целесообразно оставлять двойной промежуток после каждых пяти (и далее кратных пяти) строк.

5. Если названия отдельных граф повторяются, содержат повторяющиеся термины или несут единую смысловую нагрузку, то им необходимо присвоить общий объединяющий заголовок.

Данный прием используется и для подлежащего, и для сказуемого таблиц.

6. Графы (столбцы) и строки полезно нумеровать. Графы, заполненные названием строк, принято обозначать заглавными буквами алфавита (А, В и т.д.), а все последующие графы номерами в порядке возрастания.

7. Взаимосвязанные и взаимозависимые данные, характеризующие одну из сторон анализируемого явления (например, число библиотек вообще и удельный вес публичных, абсолютный прирост и темп роста библиотечного фонда и т.д.), целесообразно располагать в соседних друг с другом графах.

8. Графы и строки должны содержать единицы измерения, соответствующие поставленным в подлежащем и сказуемом показателям. При этом используются общепринятые сокращения единиц измерения (экз., док., назв. и т.д.).

1. Абсолютные и относительные величины, виды, методы расчета. Возможные ошибки при неправильном применении относительных величин.

Результаты статистического наблюдения регистрируются прежде всего в форме первичных абсолютных величин.

Абсолютные величины - именованные числа, которые характеризуют объем или размер предполагаемого явления или процесса. Они являются исходным материалом для изучения и анализа. Недостатки в том, что они не выражают всей совокупности и по ним нельзя делать степень сравнения (больше - меньше, чаще - реже и т.п.).

Относительные величины - производные числа от абсолютных величин, которые позволяют сравнивать или сопоставлять между собой изучаемые явления по их частоте или структуре.

Относительные величины - (О.В.) рассчитываются по формуле:

явление (часть)

О.В. = -------------------------- Х основание (100, 1000,10000)

среда (целое)

Размерность выражения: ^о/_о, ^о/_оо, ^о/_ооо, ^о/_оооо.

Виды относительных величин:

-показатель экстенсивности

-показатель интенсивности

-показатель соотношения

-показатель наглядности

а) Показатель экстенсивности - характеризует структуру изучаемого явления. Формирует его одна однородная статистическая совокупность.

б) Показатель интенсивности - характеризует частоту явления в однородной среде.

в) Показатель соотношения - характеризует частоту явления в разнородной среде.

г) Показатель наглядности - характеризует соотношение сравниваемых величин между собой, при условии, что одна из них принята за основу для сравнения за 100% или за 1.

Относительная величина в статистике – это обобщающий показатель, который дает числовую меру соотношения двух сопоставляемых абсолютных величин

Экстенсивный показатель – относительная величина, показывающая, как велика отдельная часть по отношению ко всей изучаемой совокупности; выражается в процентах, реже в промилле; используется для характеристики структуры явления, напр. возрастной структуры или структуры заболеваемости населения.

Интенсивный показатель – показатель, отражающий частоту возникновения, силу, распространенность того или иного явления в продуцирующей данное явление среде. Рассчитывается на 100, 1000, 10 000 и 100 000 населения (рождаемость, смертность, заболеваемость и др.).

Показатель наглядности - соотношене какого либо признака к другому, принятому за 100% или за единицу

1. Понятие о вариационном ряде. ( Методика составления, сгруппированный вариационный ряд, показатели анализа ).

Ряд значений признака (вариантов), расположенных в порядке возрастания или убывания с соответствующими им весами, называется вариационным рядом (рядом распределения).

В качестве весов выступают частоты или частости.

Частота (т) показывает, сколько раз встречается тот или иной вариант (значение признака) в статистической совокупности.

Частость или относительная частота (?i) показывает, какая часть единиц совокупности имеет тот или иной вариант. Частость рассчитывается как отношение частоты того или иного варианта к сумме всех частот ряда

Вариационные ряды бывают дискретными и интервальными.

V- варианты, числовые значения признака

Р- частота признака, т.е. сумма вариант с данным значением признака

n-сумма всех частот (общее число всех вариант)

Вари ряды бывают простыми-несгрупирированными (до 30наблюдений) и сложными-сгрупирированными.

Требования:

1Расположить все варианты по порядку

2Суммировать единицы, имеющие одинаковый признак, т.е. найти частоту каждой варианты

3Определить число групп и размер интервала

4Разбить весь ряд на группы, используя выбранный интервал и строго соблюдая непрерывность сгруппированного ряда

5Дать графическое изображение

i(интервал)=(Vmax-Vmin)\число групп

Вариационный ряд - ряд чисел, расположенных в определенном порядке, характеризующих один признак, но отличающихся друг от друга по своей величине.

Виды вариационных рядов:

· убывающий

· нарастающий

· неопределенный

· сгруппированный

Вариационный ряд характеризуют следующие признаки: варианта, частота, мода, медиана, амплитуда, лимит, интервал и др.

1. Виды средних величин. Возможные ошибки при их неправильном применении. Методы расчета средней арифметической простой.

Виды средних величин:

-мода

-медиана

-средняя арифметическая

-простая

-взвешенная

Мода -самая частая варианта

Медиана - варианта расположенная посередине ряда

Средней арифметической величиной называется такое среднее значение признака, при вычислении которого общий объем признака (сумма значений признака) в изучаемой совокупности сохраняется неизменным.

Средняя величина - это величина, которая средним цифровым значением характеризует изучаемое явление или признак.

Средняя арифметическая простая = сумма всех числе\количество чисел

Недостатки средних величин заключаются в том, что за ними не видно индивидуальных различий изучаемого явления.

Средние величины рассчитываются из вариационного ряда.

Средняя арифметическая простая рассчитывается из вариационного ряда, в котором каждая варианта встречается один раз. Она рассчитывается по формуле:

1. Средняя арифметическая взвешенная, понятие, методы расчета.

Взвешенная средняя арифметическая — равна отношению (суммы произведений значения признака к частоте повторения данного признака) к (сумме частот всех признаков). Используется, когда варианты исследуемой совокупности встречаются неодинаковое количество раз.

Средняя арифметическая взвешенная высчитывается из вариационного ряда, в котором каждая варианта встречается один раз и более.

Она рассчитывается: - непосредственным способом

- по способу моментов

Средняя арифметическая взвешенная непосредственным способом рассчитывается по формуле:

Средняя арифметическая взвешенная по способу моментов рассчитывается по формуле:

В процессе работы необходимо дать характеристику изучаемого явления (характеристику разнообразия признака). Разнообразие (или похожесть) характеризуют:

- амплитуда

- лимит

- среднеквадратическое отклонение

- коэффициент вариации

1. Характеристика разнообразия изучаемого признака, основные показатели, применение в медицине.

 

 

1. Методика расчета среднего квадратического отклонения. Сигмальные зоны, их применение в медицине.

Среднеквадратическое отклонение (сигма) характеризует колеблемость (вариабельность) вариационного ряда и является его абсолютной мерой. Чем большее число наблюдений будет находиться в пределах + одна сигма от средней арифметической, тем однообразнее будет вариационный ряд.

Сигма для средней арифметической, вычисленной по способу моментов, рассчитывается по формуле: