
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Проверка нормальности распределения (критерий Пирсона)
МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ ФГБОУ ВО «ПЕНЗЕНСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ АРХИТЕКТУРЫ И СТРОИТЕЛЬСТВА»
Технологический факультет Кафедра «Управление качеством и технология строительного производства»
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА к курсовой работе по дисциплине: «Статические методы контроля и управления качеством» на тему: «Статистические методы контроля и управления качеством лукума с изюмом»
Автор работы _________ Алимов А.А. Направление 27.03.02 «Управление качеством» Обозначения КР-2069059-27.03.02-200695-2023 Группа 20УК1 Руководитель работы _____________ Логанина В.И. Работа защищена _______________ Оценка ____________
Пенза 2023
Введение...................................................................................................................3 1 Статистические характеристики показателей качества продукции................4 1.2 Гистограмма....................................................................................................6 1.3 Проверка нормальности распределения (критерий Пирсона)…………...8 2 Статистическое регулирование технологических процессов........................10 2.1 Контрольные карты......................................................................................10 3 Разработка плана статического приемочного контроля.................................14 Заключение ………………………………………………………………………15 Список использованных источников …………………………………………..16
Контроль качества изделия – это процесс, направленный на выявление соответствия продукции или услуг установленным стандартам качества. Главная цель такого мероприятия – убедиться, что товары или услуги являются надежными и не имеют недостатков. В ходе проверки происходит анализ количественных и качественных характеристик, которые позволяют определить, насколько качественной является продукция. Система управления качеством продукции включает следующие функции: 1. Функции стратегического, тактического и оперативного управления. 2.Функции принятия решений, управляющих воздействий, анализа и учета, информационно-контрольные. 3. Функции специализированные и общие для всех стадий жизненного цикла продукции. 4. Функции управления по научно-техническим, производственным, экономическим и социальным факторам и условиям
«Пензенская кондитерская фабрика» – крупнейшее предприятие кондитерской промышленности Пензенской области. Фабрика основана в 1925 году. С 2003 года входит в Холдинг «Объединенные кондитеры». Фабрика оснащена современным, высокотехнологичным оборудованием, которое позволяет выпускать ассортиментный ряд кондитерских изделий для среднего ценового сегмента. Также специалисты предприятия ежегодно разрабатывают и предлагают потребителям оригинальные новинки. В настоящее время выпускается более 130 наименований изделий: конфеты, ирис, драже, зефир, вафли, пряники, печенье и вафельные торты. Визитная карточка предприятия и города Пензы – наборы элитных шоколадных конфет «Тарханы», «Сувенир из Пензы», «Дивные купола» и «Пенза». Фабрика вырабатывает не только изделия локального ассортимента, но и бренды федерального значения. Высокое качество продукции, средний ценовой сегмент, эффективная логистика, финансовая стабильность фабрики – это те преимущества, которые делают предприятие привлекательным для партнерства. Кондитерские изделия можно купить практически в любом регионе России – от Калининграда до Сахалина, от Краснодара до Архангельска. Фабрика активно развивает и поддерживает экспортное направление деятельности. На международных специализированных выставках, таких как «Продэкспо» и «World Food», в которых предприятие ежегодно принимает участие, специалистами проводятся переговоры и заключаются контракты со многими зарубежными партнерами. В планах компании –расширение ассортимента продукции.
Статистические методы управления качеством являются обязательным элементом современных систем менеджмента качества, внедряемых на российских предприятиях, конкурентоспособность которых во многом зависит от умения персонала предприятия на практике применять эти методы С помощью этих методов можно указать, где для повышения качества продукции должна быть изменена либо его структура, либо технология изготовления, а также статистические методы позволяют отрегулировать технологический процесс так, что сводится к минимуму производственный брак. Управлять качеством продукции необходимо на основе объективной информации об осуществлении технологических процессов.
В данном разделе приводятся сведения о показателях качества продукции. Необходимо провести измерения показателей качества. Следует рассчитать статистические характеристики выборки: средняя арифметическая величина, размах, среднеквадратическое отклонение, коэффициент вариации. Продукция-пастила фабрики ЗАО «Пензенская кондитерская фабрика» должна соответствовать следующим требованиям: Плотность, г\см3 не более 0,8; влажность, % не более 25 Массовая доля редуцирующих веществ, % от 10 до 25 В таблице 1 приведены статические данные плотность, г\см3 в пастиле:
Таблица 1 Влажность, %
День Влажность, % День Влажность, % День Влажность, % День Влажность, % День Влажность, % День Влажность, % 20,1 21,6 20,9 23,8 22,5 22,4 21,2 22,7 22,2 21,5 21,8 22,4 20,4 20,4 21,7 20,2 21,7 22,4 22,8 21,4 20,5 21,1 20,6 20,6 21,9 22,3 22,3 20,9 21,3 20,2 20,6 22,9 21,3 22,7 21,3 20,5 21,3 21,7 22,2 20,2 20,4 22,2 21,6 20,6 20.9 22,5 21,8 21,9 22,9 20,5 21,5 21,5 22,4 20,3 21,9 20,1 20,4 20,7 20,8 51 20,6 22,3 21,1 21,5 20,6 22,3 22,7 21,4 20,9 Продолжение таблицы 1
Влажность, % 20,6 21,2 22,7 20,9 20,6 22,6 20,8 21,3
Имеются две важнейшие характеристики, которые отражают результат исследований: одна из них описывает среднее положение наблюдаемых значений, а другая – отклонения единичных измерений от средней. Если в результате n измерений получены значения x1, x2, …, xn, то средняя арифметическая величина: Среднее квадратическое отклонение s.
1.2 Гистограмма
Гистограммой называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которых служат частичные интервалы длиной h, а высоты- это плотность частоты. Для построения гистограммы частот на оси абсцисс откладывают частичные интервалы, а над ними проводят отрезки, параллельные оси абсцисс на расстоянии Площадь i-го частичного прямоугольника равна
Тогда ширина интервала:
Таблица 2 – Значения плотности частоты Частичный интервал длиной h=1,4 Сумма частот вариант частичного интервала ni [20-20,4) [20,4-20,8) [20,8-21,2) [21,2-21,6) [21,6-22) [22-22,4) [22,4-22,8) [22,8-23,2)
Рисунок 1 – Гистограмма влажность, %
Суть критерия Пирсона состоит в вычислении критерия
где k — это число разрядов наблюдаемых значений, а Алгоритм критерия Пирсона несложен и состоит в выполнении следующих действий: - сначала по данным выборки получают статистическое распределение наблюдаемого признака; - затем — вычисляют теоретические частоты признака, какими они должны были бы быть, если бы признак был действительно распределен в соответствии с данным законом; - по данной выше формуле вычисляют эмпирическое значение критерия
- по таблице критических значений критерия Пирсона определяют - в случае, если
Проверим гипотезу о том, что Х распределено по нормальному закону с помощью критерия согласия Пирсона.
Для вычисления вероятностей pi применим формулу и таблицу функции Лапласа
Таблица 3 Данные расчета по критерию Пирсона
xi÷xi+1 fi x1 = (xi - xср)/s x2 = (xi+1 - xср)/s Ф(x1) Ф(x2) pi=Ф(x2)-Ф(x1) Ожидаемая частота, 91pi Слагаемые статистики Пирсона, Ki 20 - 20.4 -1.679 -1.2096 -0.4535 -0.3869 0.0666 6.0606 4.0256 20.4 - 20.8 -1.2096 -0.7402 -0.3869 -0.2734 0.1135 10.3285 3.1143 20.8 - 21.2 -0.7402 -0.2708 -0.2734 -0.1103 0.1631 14.8421 0.2286 21.2 - 21.6 -0.2708 0.1986 -0.1103 0.0793 0.1896 17.2536 0.6135 21.6 - 22 0.1986 0.668 0.0793 0.2486 0.1693 15.4063 1.8972 22 - 22.4 0.668 1.1374 0.2486 0.3729 0.1243 11.3113 0.00857 22.4 - 22.8 1.1374 1.6068 0.3729 0.4463 0.0734 6.6794 2.7948 22.8 - 23.2 1.6068 2.0762 0.4463 0.4812 0.0349 3.1759 1.0477 13.7303
Определим границу критической области. Так как статистика Пирсона измеряет разницу между эмпирическим и теоретическим распределениями, то чем больше ее наблюдаемое значение Kнабл, тем сильнее довод против основной гипотезы. Поэтому критическая область для этой статистики всегда правосторонняя: [Kkp;+∞). Её границу Kkp = χ2(k-r-1;α) находим по таблицам распределения χ2 и заданным значениям s, k (число интервалов), r=2 (параметры xcp и s оценены по выборке). Kkp = χ2(8-2-1;0.05) = 11.07050; Kнабл = 13.73 Наблюдаемое значение статистики Пирсона попадает в критическую область: Кнабл > Kkp, поэтому есть основания отвергать основную гипотезу. Данные выборки распределены не по нормальному закону.
2.1 Контрольные карты Статистические методы регулирования позволяют своевременно выявить разладку технологического процесса и тем самым предупредить выпуск дефектной продукции. В результате реализуется важнейшее требование стандартов ИСО серии 9000 – «предупреждать любое несоответствие продукции».
Контрольные карты подразделяют на три основных вида: - карты Шухарта - приемочные - адаптивные. Все эти контрольные карты работают с выборочными данными по количественному или альтернативному признаку. Приемочные карты позволяют осуществлять одновременно две процедуры: - слежение за ходом технологического процесса и его регулирование; - контроль продукции, направленный на то, чтобы фактический уровень несоответствий данной продукции не превышал установленного уровня несоответствий NQL. В зависимости от того, по каким статистическим характеристикам осуществляют статистическое регулирование, различают следующие виды контрольных карт Шухорта: 1 Карта средних арифметических значений 2 Карта медиан 3 Карта среднеквадратических отклонений 4 Карта размахов 5 Карта доли дефектных единиц продукции 6 Карта числа дефектных единиц продукции 7 Карта числа дефектов 8 Карта числа дефектов на единицу продукции Логика работы с контрольными границами следующая: 1. Если точка на контрольной карте лежит внутри контрольных границ, то считается, что все колебания точек здесь объясняются чисто случайными факторами. 2. Если же одна (или несколько) точка выходит за контрольные границы, то считается, что такие отклонения не могут произойти случайно, т.е. здесь имеет место воздействие случайного фактора.
При контроле по количественному признаку о разладке технологического процесса судят как по среднему значению контролируемого параметра, так и по рассеиванию значений контролируемого параметра относительно этого среднего значения. Смещение среднего значения (в любую сторону) относительно середины поля допуска и увеличение рассеивания приводит к увеличению доли дефектной продукции. В качестве средних значений при статистическом регулировании используем среднее арифметическое значение. В качестве характеристик рассеивания при статистическом регулировании используем среднее квадратическое отклонение. При статистическом регулировании технологического процесса при контроле по количественному признаку воспользуемся двойными контрольными картами, на одной из которых отмечены средние значения, а на другой – характеристику рассеивания, что позволит непрерывно следить за составляющими общей дисперсии – рассеянием внутри мгновенных выборок и рассеянием между значениями средней арифметической различных выборок. После чего можно сделать вывод о статистическом управлении процессом, только в том случае, когда об этом свидетельствуют обе карты. В результате предварительного исследования состояния технологического процесса решают следующие задачи: - получают оценки параметров нормального распределения (ɑ и σ);
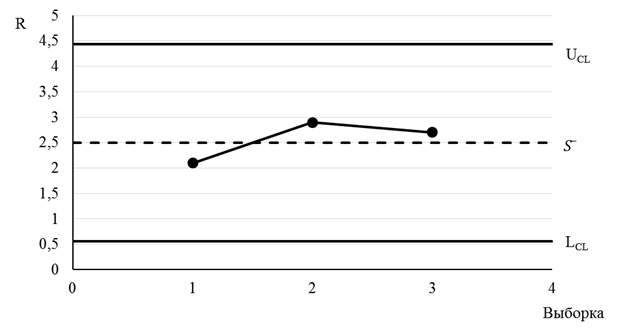
- определяют вероятную долю дефектной продукции (ρ). Для анализа стабильности технологического процесса воспользуемся x–r – картой.
Таблица 4 – Распределение выборок
№ Номер выборки 𝑥1 20,1 22,4 21,3 𝑥2 20,7 21,6 𝑥3 22,2 21,5 22,9 𝑥4 20,4 20,3 𝑥5 21,4 𝑥6 21,5 20,6 𝑥7 20,6 21,7 21,6
20,5 20,5 22,4 𝑥9 22,2 22,3 21,8 𝑥10 21,9 22,9 20,2
21,23 21,45 21,47
ВД=30; НД=15
ВГР= R1=2,1 R2=2,9 R3=2,7
Вычисление границ регулирования для r – карты:
ВГР=1,777*2,5=0,557 НГР=0,223*2,5=4,442
Из полученных результатов можно сделать вывод, что процесс стабилен и находится в статистически воспроизводимом состоянии, так как на х и r картах точки не выходят за границы регулирования.
Объем партии 90 шт. (смена). Объем партии 7. Уровень дефектности продукции 1,5% K=1,5 НД=0,3 ВД=0,8 0,7; 0,5; 0,5; 0,3; 0,6; 0,5; 0,6;
S= Qв= Qн= 0,2+(k*s)=0,2+1,5*0,13)=0,495 0,8-(k*s)=0,8-0,195=0,605 Так как Графический способ решения S-плана
Исследование статистических методов помогает изучить протекание технологического процесса. Благодаря чему в результате получают наилучшее выполнение требований качественных показателей изделий. Это также способствует уменьшению брака, повышению производительности труда и снижению себестоимости. Эти методы помогают узнать в какой именно момент и кем вызваны те или иные помехи в производственном процессе. В рамках данного курсового проекта я приобрел комплекс специальных знаний и умений, необходимых для проектирования и организации надежных и стабильных производственных процессов, обеспечивающих изготовление качественной продукции.
1 Логанина В.И. Статические методы контроля и управления качеством продукции: учебное пособие. – Пенза: ПГУАС, 2012. – 96 с.; 2 ГОСТ Р 50779.71-99 Статистические методы. Процедуры выборочного контроля по альтернативному признаку. Часть 1. Планы выборочного контроля последовательных партий на основе приемлемого уровня качества AQL. – Введ. 2000-07-01-М: ИПК Издательство стандартов,2000. - 68стр.; 3 Логанина В.И., Петухова Н.А., Садовникова М.А. Статистические методы контроля и управления качеством: указания для выполнения курсового проекта. - Пенза: ПГУАС, 2017. - 32 с.
|
|||||||||
|
Последнее изменение этой страницы: 2024-06-27; просмотров: 7; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.155.227 (0.01 с.) |
 Содержание
Содержание Введение
Введение 1.Статистические характеристики выборки
1.Статистические характеристики выборки День
День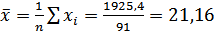
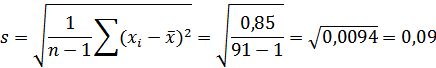
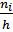 .
.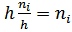 – сумме частот вариант i-го интервала; следовательно, площадь гистограммы частот равна сумме всех частот, т.е. объему выборки.
– сумме частот вариант i-го интервала; следовательно, площадь гистограммы частот равна сумме всех частот, т.е. объему выборки. Результаты измерения располагают в порядке возрастания, т.е. составляют вариационный ряд.
Результаты измерения располагают в порядке возрастания, т.е. составляют вариационный ряд.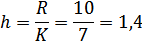
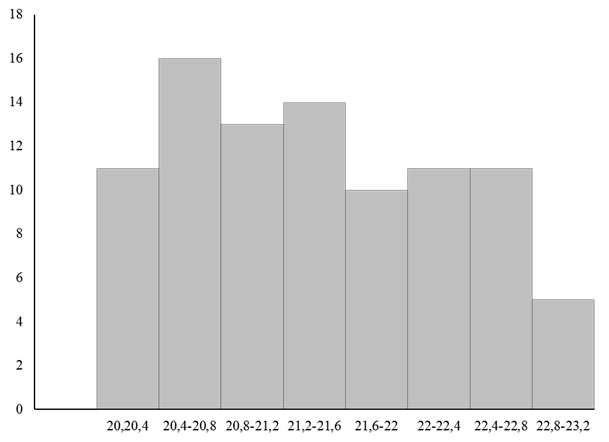
 На гистограмме видно как изменяется влажность, % лукума с изюмом. Далее проведем анализ нормальности распределения по критерию Пирсона.
На гистограмме видно как изменяется влажность, % лукума с изюмом. Далее проведем анализ нормальности распределения по критерию Пирсона.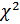 по следующей формуле:
по следующей формуле: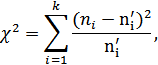
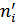 — теоретические частоты соответствующих значений.
— теоретические частоты соответствующих значений.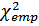 ;
;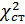 на необходимом уровне значимости
на необходимом уровне значимости  и при заданном числе степеней свободы s. Число степеней свободы вычисляется по формуле
и при заданном числе степеней свободы s. Число степеней свободы вычисляется по формуле 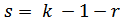 , где k — число разрядов наблюдаемых значений, r — число параметров предполагаемого распределения, в случае нормального или равномерного распределения r = 2;
, где k — число разрядов наблюдаемых значений, r — число параметров предполагаемого распределения, в случае нормального или равномерного распределения r = 2;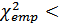
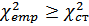 , принимают альтернативную гипотезу: статистическое распределение отличается от данного.
, принимают альтернативную гипотезу: статистическое распределение отличается от данного.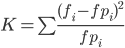
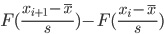


 2 Статистическое регулирование технологических процессов
2 Статистическое регулирование технологических процессов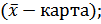
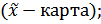
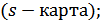
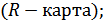
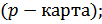
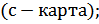
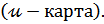
 Контрольные карты для количественных признаков. Порядок построения и анализа контрольных карт:
Контрольные карты для количественных признаков. Порядок построения и анализа контрольных карт: 𝑥8
𝑥8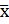
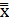 =21,4
=21,4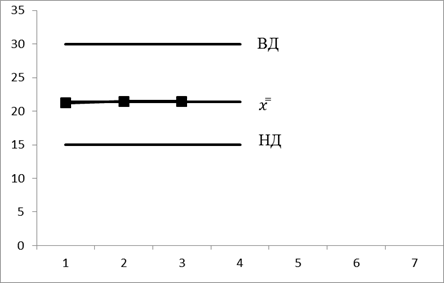
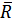 =
= 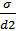 ; 2,5=
; 2,5= 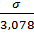
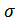 =0,81
=0,81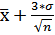 =21,4+
=21,4+ 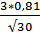 =21,843; НГР= 20,957
=21,843; НГР= 20,957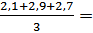 2,5
2,5
 3 Разработка плана статического приемочного контроля
3 Разработка плана статического приемочного контроля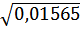 =0,13
=0,13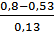 =2,08>k
=2,08>k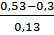 =1,77>k
=1,77>k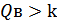 , то партия принимается.
, то партия принимается.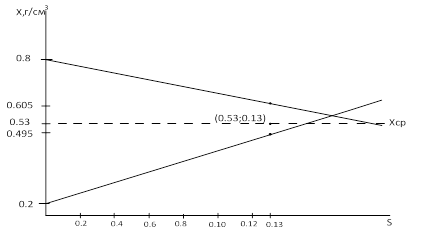
 Заключение
Заключение Список использованных источников
Список использованных источников


